POJ-1741 树上分治--点分治（算法太奇妙了)

给你1e5个节点的树，(⊙﹏⊙)

你能求出又几对节点的距离小于k吗？？（分治NB！）

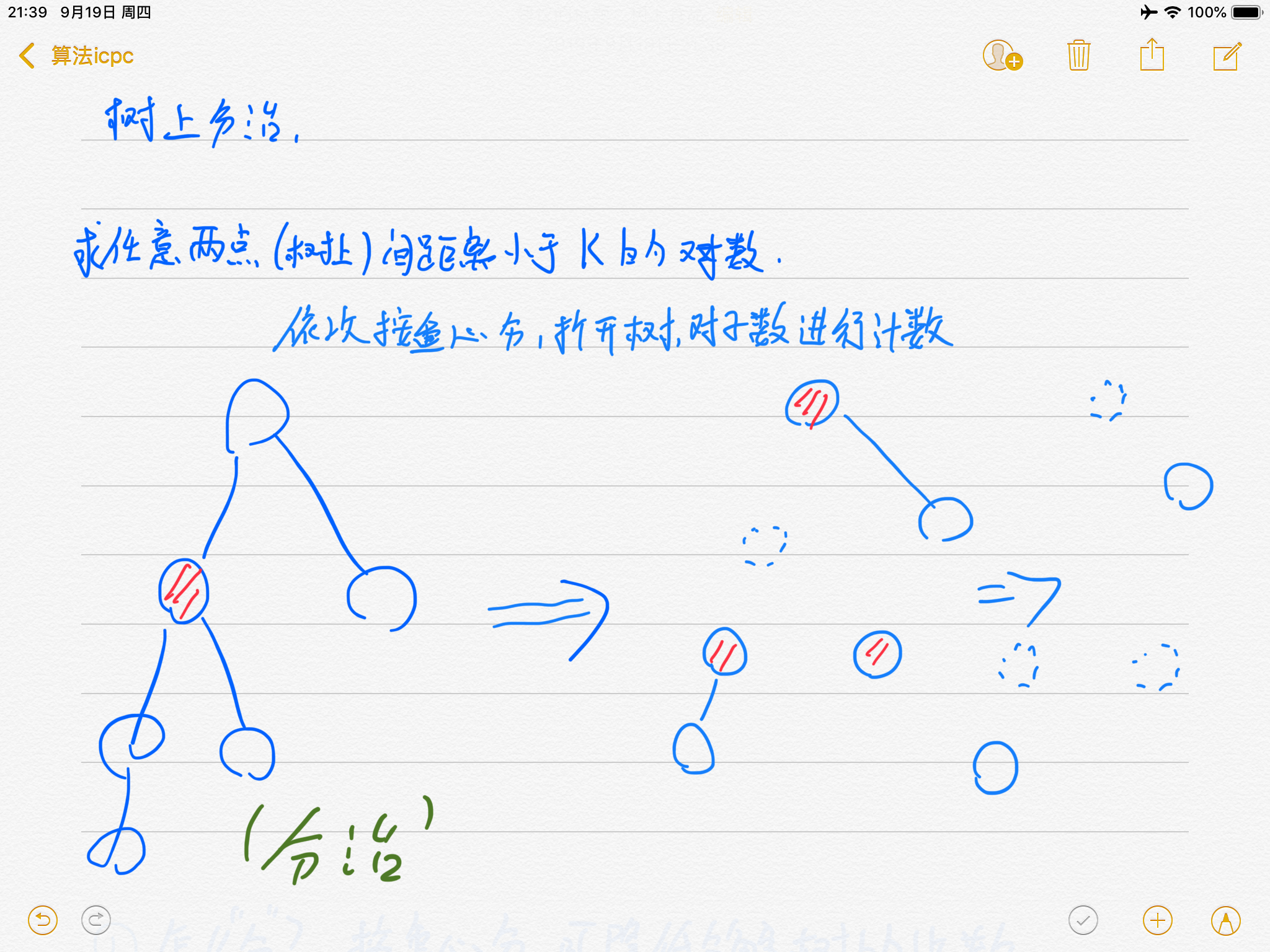
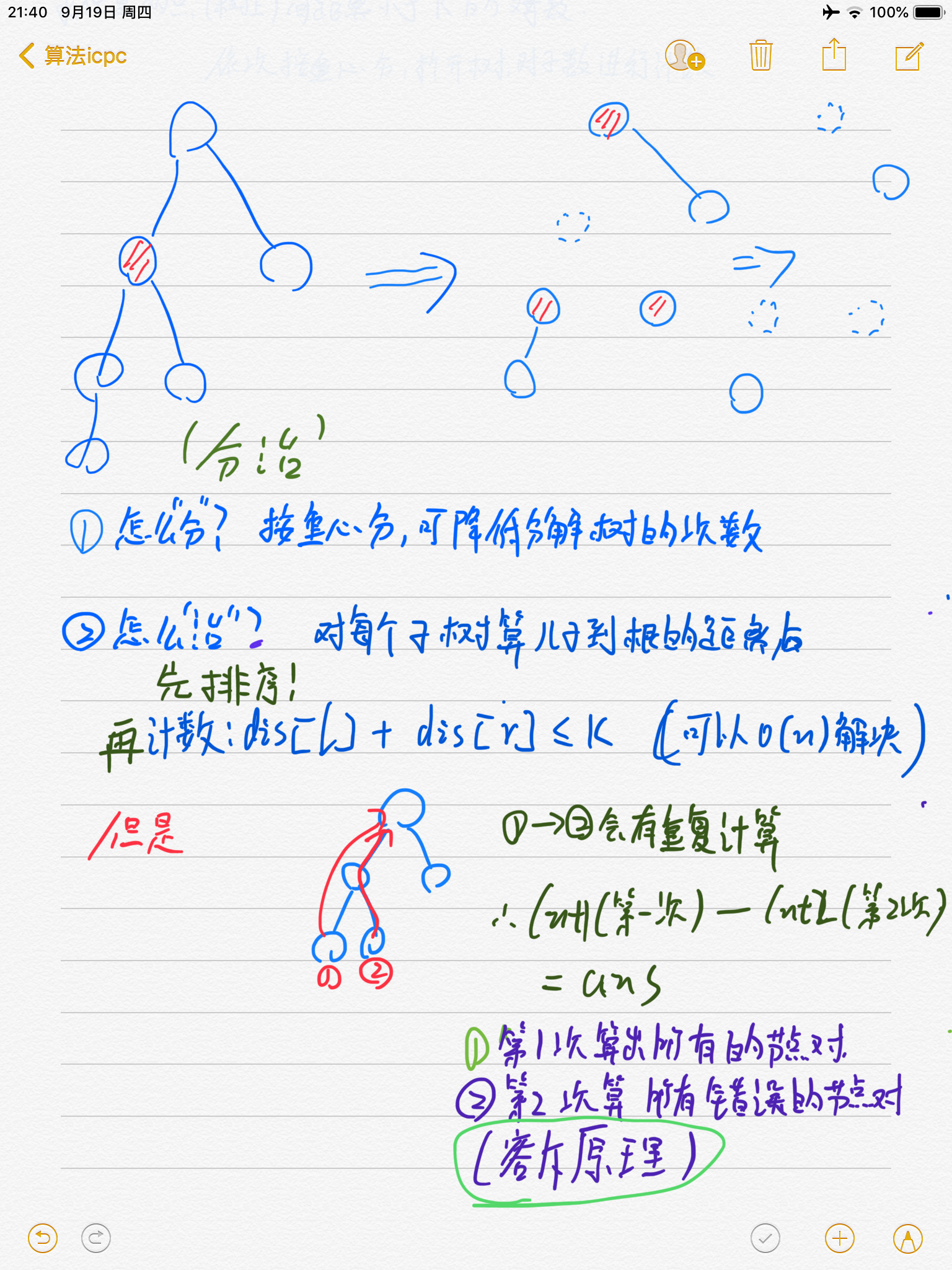
这只是一个板子题，树上分治没有简单题呀！（一个大佬说的）

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
#define maxn 10020
using namespace std;
struct Node {
	int p;
	int val;
	Node(int _p, int _val) :p(_p), val(_val) {}
};
vector<Node>G[maxn];
void insert(int be, int en, int len) {
	G[be].push_back(Node(en, len));
}
int dis[maxn];//距离
int son[maxn];
int ans[maxn];
int vis[maxn];
int d[maxn];
int chal;
int k;
int n;
int cntv = 0;
int root;
int ln = 0;

void find_root(int x, int fa) {//找重心
	son[x] = 1;
	ans[x] = 0;
	for (int i = 0; i < G[x].size(); i++) {
		int p = G[x][i].p;
		if (p == fa || vis[p]) continue;
		find_root(p, x);
		son[x] += son[p];
		ans[x] = max(son[p], ans[x]);
	}
	ans[x] = max(cntv - son[x], ans[x]);//cntv当前树重量

	if (ans[x] < ans[root]) root = x;	//尽量小
}

void get_dis(int x, int fa) {//计算各个点到根的距离
	dis[ln++] = d[x];
	for (int i = 0; i < G[x].size(); i++) {
		int p = G[x][i].p;
		if (fa == p || vis[p]) continue;
		d[p] = d[x] + G[x][i].val;
		get_dis(p, x);
	}

}
int cal(int x, int val) {//val要是零，x就是根，否则就是子树
	d[x] = val;
	ln = 0;
	get_dis(x, 0);
	sort(dis, dis + ln);
	int l = 0, r = ln - 1, res = 0;
	while (l < r) {
		if (dis[l] + dis[r] <= k) {
			res += r - l;
			l++;
		}
		else r--;
	}
	return res;
}
int slove(int x) {
	chal += cal(x, 0);
	vis[x] = 1;
	for (int i = 0; i < G[x].size(); i++) {
		int p = G[x][i].p;
		if (vis[p]) continue;
		chal -= cal(p, G[x][i].val);
		cntv = son[p];
		root = 0;
		ans[0] = 0x3f3f3f3f;
		find_root(p, 0);
		slove(root);
	}
	return 0;
}
int main() {
	int be, en, len;
	while (~scanf("%d%d", &n, &k)) {
		if (n == 0 && k == 0) break;
		memset(vis, 0, sizeof(vis));
		ans[0] = 0x3f3f3f3f;
	//	memset()
		for (int i = 0; i <= n; i++) G[i].clear();
		for (int i = 0; i < n - 1; i++) {
			scanf("%d %d %d", &be, &en, &len);
			insert(be, en, len);
			insert(en, be, len);
		}
		root = 0;
		cntv = n;
		find_root(1, 0);
		chal = 0;
		slove(root);
		printf("%d\n", chal);
	}
	return 0;
}