lattice planner 规划详解

大家好，我是来自百度智能驾驶事业群的许珂诚。今天很高兴能给大家分享Apollo 3.0新发布的Lattice规划算法。

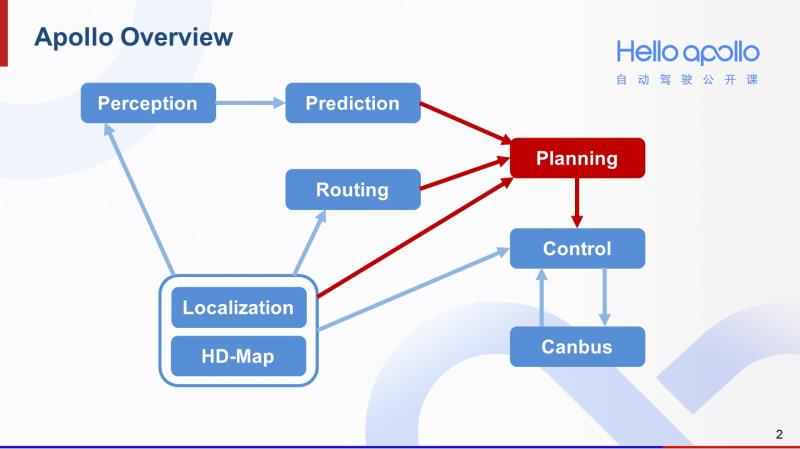
Lattice算法隶属于规划模块。规划模块以预测模块、routing模块、高精地图和定位的结果作为输入，通过算法，输出一条平稳、舒适、安全的轨迹，交给控制模块去执行。我们可以看到，规划模块在Apollo中是一个承上启下的重要模块。

Lattice算法隶属于规划模块。规划模块以预测模块、routing模块、高精地图和定位的结果作为输入，通过算法，输出一条平稳、舒适、安全的轨迹，交给控制模块去执行。我们可以看到，规划模块在Apollo中是一个承上启下的重要模块。

一个合格规划算法，必须满足几个条件。首先，必须能够使自动驾驶汽车到达目的地；其次，必须符合交规；第三，能够避免碰撞；最后，也需要能保证一定的舒适性。

在Apollo中，规划算法的输出是一系列轨迹点连成的轨迹。每一个轨迹点包含位置，速度，加速的等信息。

下面我来介绍一下Lattice规划算法的工作流程。我们以右图中的场景为例。其中红车是我们的自动驾驶汽车，蓝车是其他障碍车，前面蓝色带尖头的曲线是蓝车的预测轨迹。那么这是一个前方即将有车辆并入的场景。

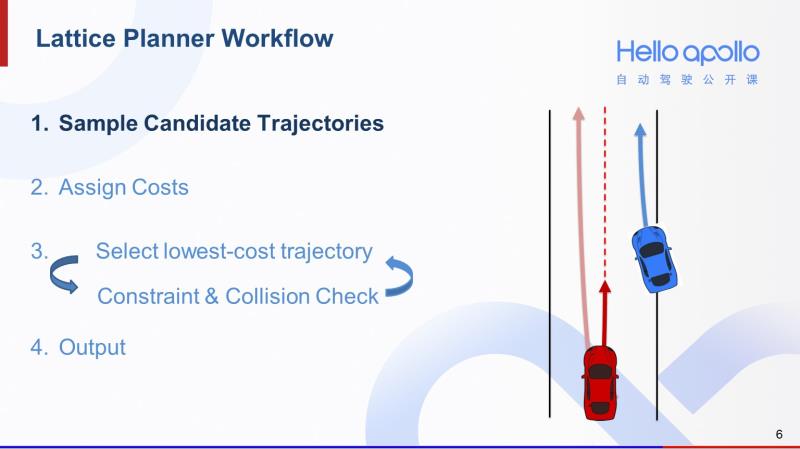
面对这样的场景，有些司机会按照右图中浅红色的轨迹，选择绕开蓝色的障碍车。另外有一些司机开车相对保守，会沿着右图中深红色较短的轨迹做一个减速，给蓝色障碍车让路。

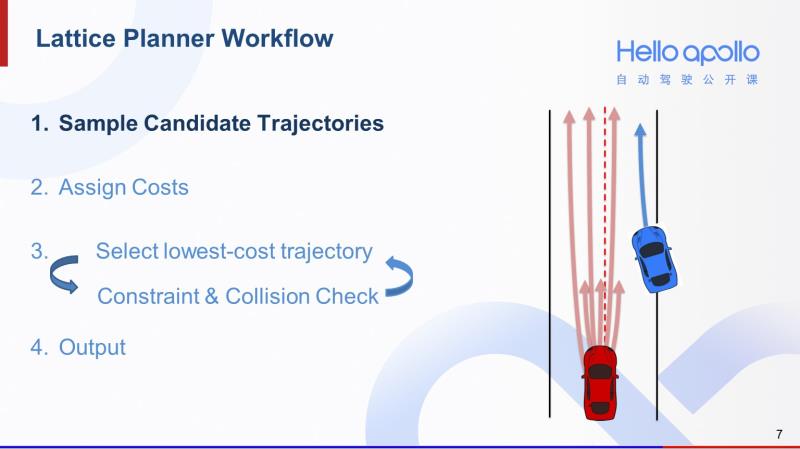
既然对于同一个场景，人类司机会有多种处理方法，那么Lattice规划算法的第一步就是采样足够多的轨迹，提供尽可能多的选择

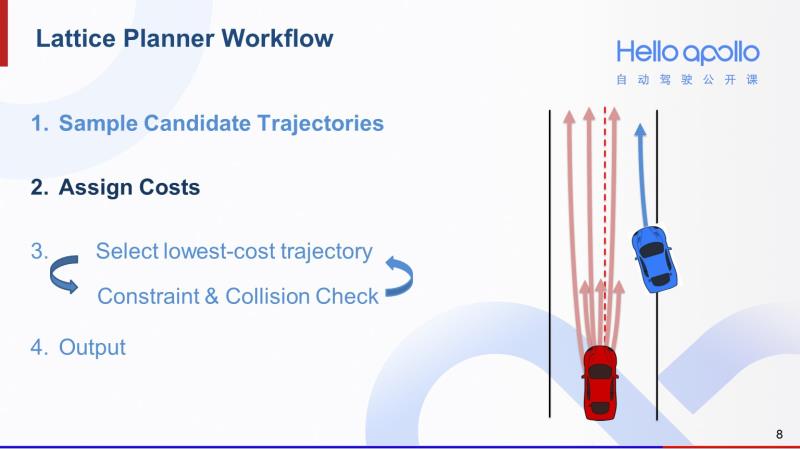
Lattice规划算法的第二步是计算每一条轨迹计算的cost。这个cost考虑了轨迹的可行性、安全性等因素。我会在后面为大家详细介绍。

那么有了轨迹的cost以后，第三步就是一个循环检测的过程。在这个过程中，我们每次会先挑选出cost最低的轨迹，对其进行物理限制检测和碰撞检测。如果挑出来的轨迹不能同时通过这两个检测，就将其筛除，考察下一条cost最低的轨迹。

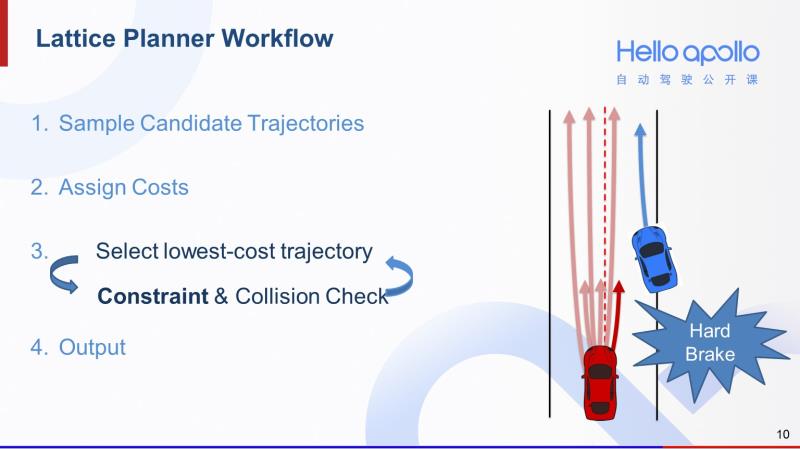
以右图为例，假设我们首先挑选出cost最低的是深红色较短的轨迹。但我们发现即便猛踩刹车也无法执行这条轨迹。也就是说，这条轨迹超出了汽车的减速度上限。那么它就无法通过物理限制检测，我们会将其筛除。

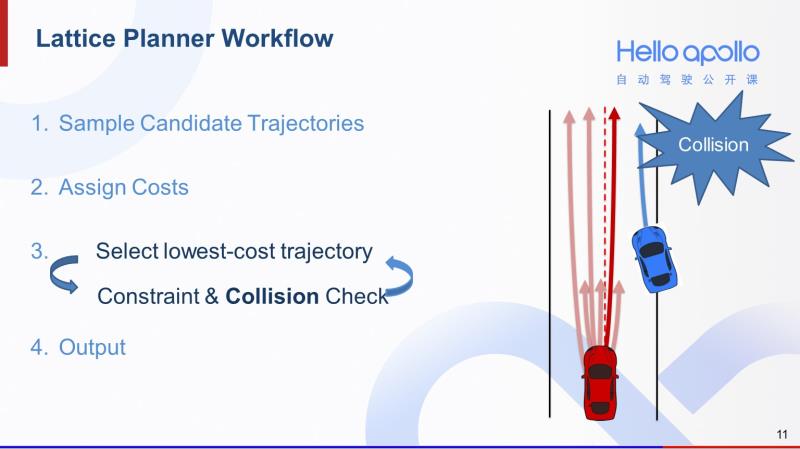
假设我们下一条选出来cost最低的轨迹是右图中深红色较长的轨迹。我们会发现若沿着这条轨迹前进，红车会和蓝色障碍车发生碰撞。也就是说，这条轨迹轨迹无法通过碰撞检测。于是只能放弃这条轨迹，考虑下一条cost最低的。

这样的过程循环继续下去，假设我们现在挑选出右图中靠左边的深红色轨迹，它既符合汽车的物理性状，也不会有碰撞风险。

我们最终就将这条轨迹作为规划轨迹输出。
那么下面我们对每一个步骤，进行详细的说介绍。

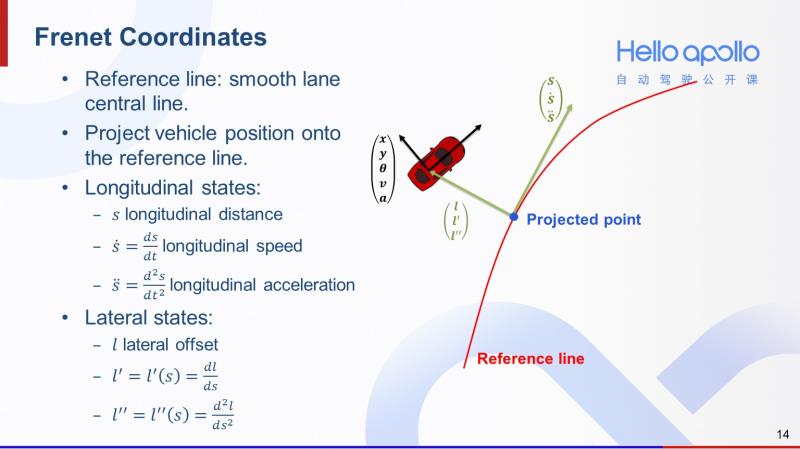
首先是采样过程。在正式介绍采样过程之前，作为铺垫，我先来介绍一下Frenet坐标系。在二维平面中，我们通常采用X-Y坐标系来描述问题。但在自动驾驶规划问题中，我们的工作是基于道路的。这种情况下，X-Y坐标系并不是最方便的。所以我们这里需要使用基于车道线横向和纵向的Frenet坐标系。

那么如何用Frenet坐标系来表示一辆汽车的状态呢？首先我们有一条光滑的参考线（右图中红线），我们可以按右图所示将汽车的坐标点投影到参考线上，得到一个参考线上的投影点（图中蓝色点）。从参考线起点到投影点的路径长度就是汽车在Frenet坐标系下的纵向偏移量，用S表示。而投影点到汽车位置的距离则是汽车在Frenet坐标系下的横向偏移量，用L表示。因为参考线是足够光滑的，我们也可通过汽车的朝向、速度、加速度来计算出Frenet坐标系下，横向和纵向偏移量的一阶导和二阶导。

这里需要注意的是，我们将横向偏移量L设计成纵向偏移量S的函数。这是因为对于大多数的汽车而言，横向运动是由纵向运动诱发的。

有了Frenet坐标系的概念，我们下面来介绍一下如何生成一条轨迹。首先我们可以通过计算得到自动驾驶汽车在Frenet坐标系下的在零时刻的起始状态，也就是汽车的当前状态。为了生成一条轨迹，第一步就是在Frenet坐标系下采样一个在T1时刻的末状态。

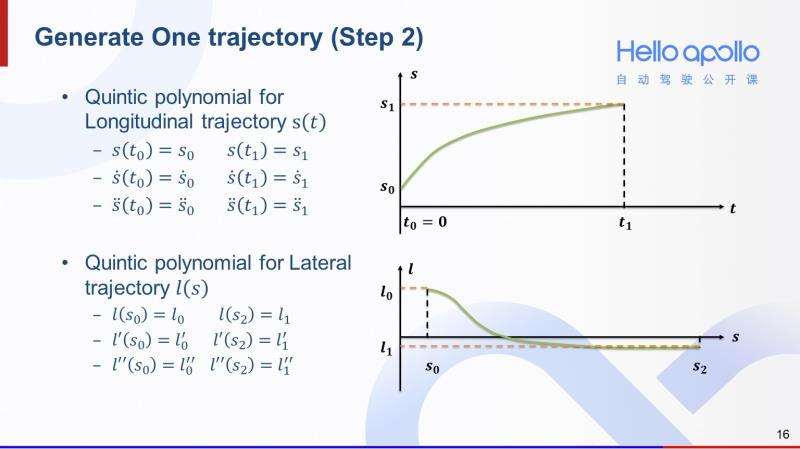
第二步就是将末状态和起始状态做多项式拟合。分别形成横向和纵向的多项式轨迹。

有了横向轨迹和纵向轨迹之后，第三步就是二维合成。给定一个时刻T*，我们可以计算出在T*时刻的纵向偏移量和横向偏移量，再通过参考线，即可还原成一个二维平面中的轨迹点。通过一系列的时间点T0，T1，...，Tn，可以获得一系列的轨迹点P0，P1，…，Pn，最终形成一条完整的轨迹。了解了如何生成一条轨迹之后，下面我来介绍一下如何采样一系列轨迹。

首先介绍如何采样横向轨迹。横向轨迹的采样需要涵盖多种横向运动状态。现在Apollo的代码中设计了三个末状态横向偏移量，-0.5，0.0和0.5，以及四个到达这些横向偏移量的纵向位移，分别为10，20，40，80。用两层循环遍历各种组合，再通过多项式拟合，即可获得一系列的横向轨迹。

对于纵向轨迹的采样，我们需要考虑巡航、跟车或超车、停车这三种状态。

在停车状态中，给定停车点，末状态的速度和加速度都是零，所以末状态是确定的。
那么我们只需用一层循环来采样到达停车点的时间即可。

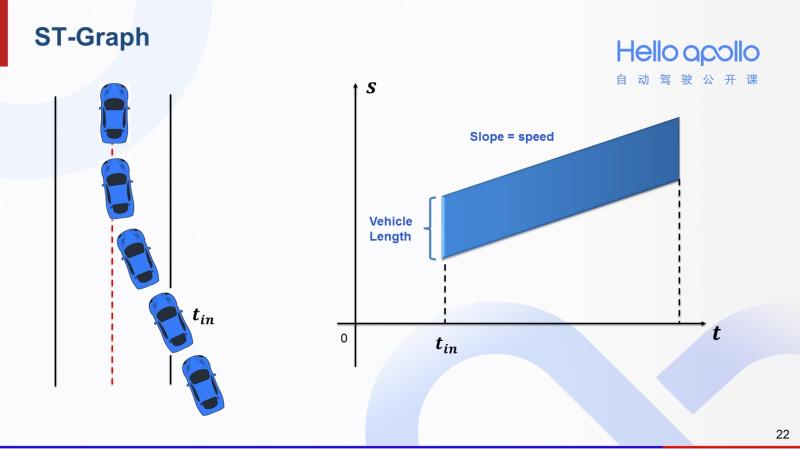
在介绍跟车/超车的采样逻辑之前，我们需要介绍一下S-T图的概念。以左图中的场景为例，蓝色障碍车从车道右侧切入，在T_in时刻开始进入当前车道。那么这个场景对应的S-T图就如右图所示。从T_in时刻开始出现一块斜向上的阴影区域。这块阴影区域的高度就是蓝色障碍车的车身长，上边界表示车头，下边界表示车尾，斜率表示车速。

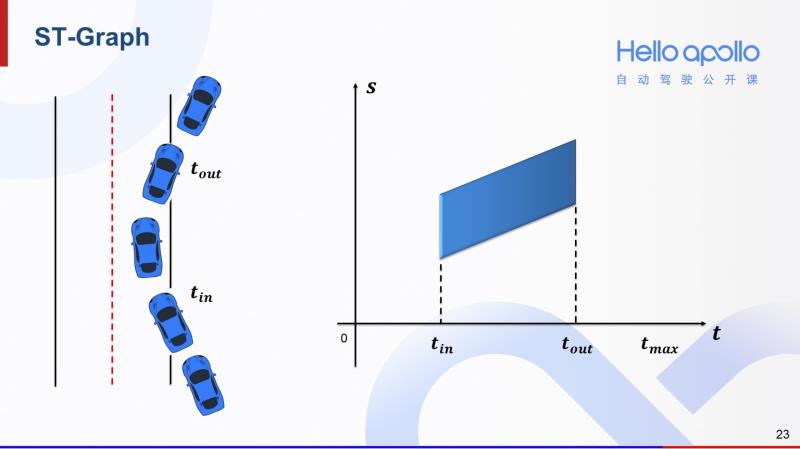
如果上述场景变成这样，障碍车从T_in时刻进入车道，然后在T_out时刻离开车道。那么这个场景对应的S-T图就会缩短。

有了S-T图的概念，我们观察左图中的两条规划轨迹。红色的是一条跟车轨迹，绿色的是超车轨迹。这两条轨迹反映在S-T图中，就如右图所示。红色的跟车轨迹在蓝色阴影区域下方，绿色的超车轨迹在蓝色阴影区域上方。

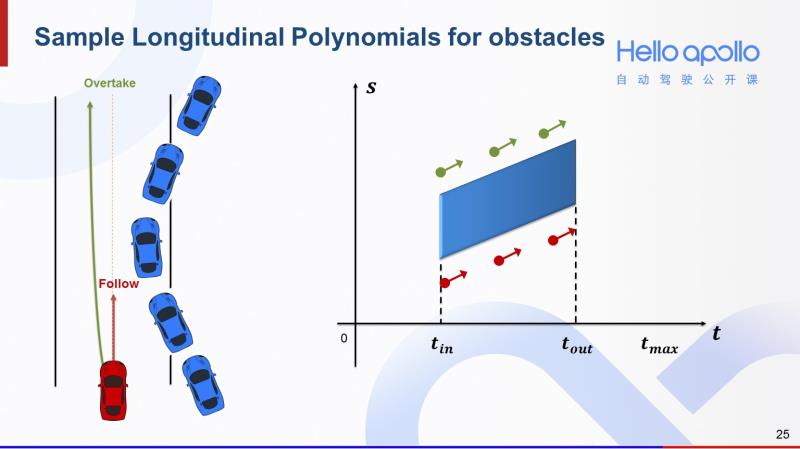
我们采样末状态时，就可以分别在S-T图中障碍物对应的阴影区域的上方和下方分别采样。上方的末状态对应超车，下方的末状态对应跟车。

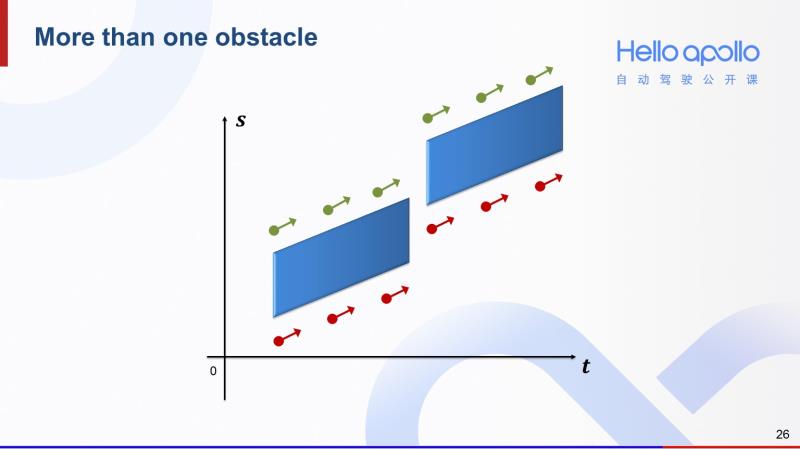
如果有多个障碍物，我们就对这些障碍物分别采样超车和跟车所对应的末状态。

那么总结下来就是遍历所有和车道有关联的障碍物，对他们分别采样超车和跟车的末状态，然后用多项式拟合即可获得一系列纵向轨迹。

我们将三组纵向轨迹组合起来，就可以获得所有纵向轨迹。再将所有纵向轨迹和所有横向轨迹两两配对二维合成，就可以完成轨迹采样的工作。

现在我们来介绍一下轨迹的cost的实现方法。我们前面提到，轨迹规划所需要满足的四点要求，分别是到达目的、符合交规，避免碰撞、平稳舒适。针对这四点要求，我们设计了六个cost，cost越高就表示越不满足要求。下面我们一一介绍这六个cost的设计思路。

首先是到达目的的cost。这里分成两种情况，一个是存在停车指令（比如红灯）的情况，另一个是没有停车指令的。如果存在停车指令，相对大的车速，其对应的轨迹cost就越大；如果没有停车指令，那么低速轨迹的cost就会越大。

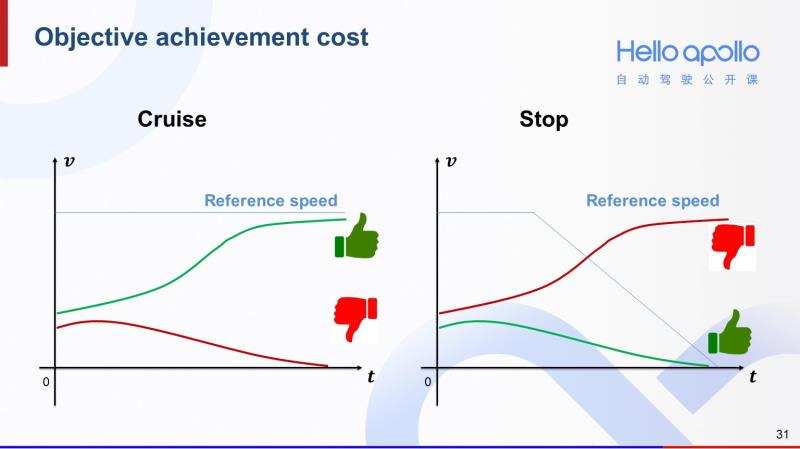
怎么实现这样的效果呢？我们针对这两种情况分别设计了参考速度。左图蓝线表示没有停车指令时的参考速度。

我们可以看到这种情况下，绿色的加速轨迹会获得一个较小的cost，而红色的减速轨迹会获得一个相对较大的cost。那么如果存在停车指令，参考速度就会想右图中的蓝色曲线一样呈下降趋势。那么这种情况下，同样的两条轨迹，他们的cost大小关系就会正好相反。

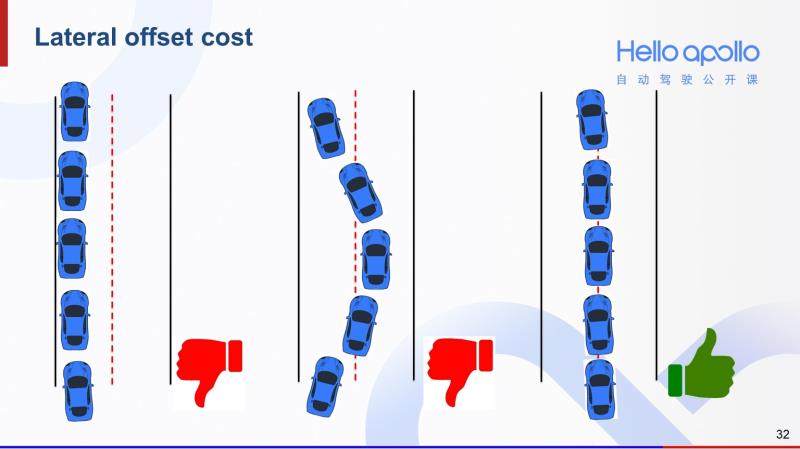
第二个cost是横向偏移cost。设计这个cost是为了让自动驾驶汽车能尽量沿着道路中心行驶。那么像左图汽车靠道路一边行驶，和中图画龙的行驶轨迹，他们的cost都相对较高。

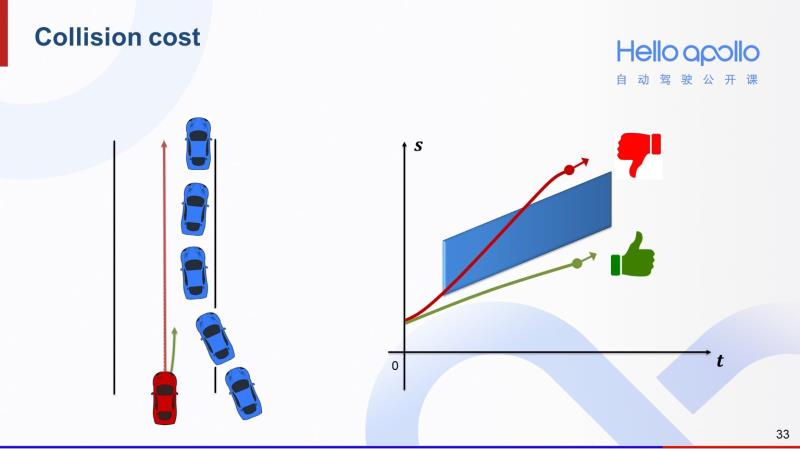
第三个cost是碰撞cost。左图中的两条轨迹，反映在右图S-T图中，我们可以发现红色的轨迹和蓝色障碍车在S-T图中的阴影区域有重叠，说明有碰撞风险，那么它的碰撞cost就会相对较高。而绿色的轨迹在S-T图中反映出来的碰撞风险较小，那么它的碰撞cost就相对较低。

第四个cost是纵向加加速度的cost。加加速度（jerk）是加速度对时间的导数，表示加速度的变化率。我们用加加速度的最大值值来表示这个cost。

第五个cost是横向加速度的cost。设计这个cost是为了平稳地换道。那么像左图猛打方向盘的轨迹，它的横向加速度cost就会相对较大。

最后一个cost是向心加速度cost。设计这个cost是为了在转弯或调头的时候能够减速慢行。在弯道处，车速慢的轨迹，其向心加速度cost就会相对较低，那么就会更容易被率先挑选出来。

这六个cost的加权求和就是轨迹的总cost。开发者可以根据产品的需要，调试这六个权重。

这里介绍一下限制检测和碰撞检测。限制检测考察的内容有轨迹的加速度、加加速度、和曲率。碰撞检测则是把自动驾驶汽车的轨迹和其他障碍物的预测轨迹进行比对，观察是否有轨迹重叠。

对于换道场景，Lattice算法仅仅需要对目标车道对应的参考线做一次采样+选择的流程。本车道和目标车道均能产生一条最优轨迹。给换道轨迹的cost上增加额外的车道优先级的cost，再将两条轨迹比较，选择cost较小的那条即可。

Lattice规划算法已经在新石器无人驾驶微型物流车和长沙智能驾驶研究院重卡中落地。我们也将继续深度合作，提高技术的同时，拓展更多产品的应用。

以上就是Lattice Planner规划算法的介绍和分享。非常感谢大家的参加！也欢迎大家提出问题，进行交流。更多Apollo相关的技术干货也可以继续关注后续的社群分享。