洛谷P3195 玩具装箱

P3195 [HNOI2008]玩具装箱TOY

第一道斜率优化题。

首先一个基本的状态转移方程是

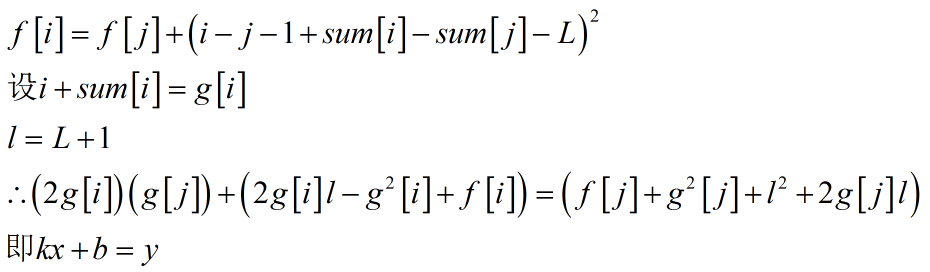
要使f[i]最小，即b最小。

对于每个j，可以表示为一个点。

然后我们取固定斜率时截距最小的即可，高中线性规划。

单调队列维护下凸包。

然后每次二分出j，转移。

记得给(0，L * L)赋初值。

记得开long long

++，--最好别随便用，编译器的不同会让你爆0...

 #include <cstdio>
 
 typedef long long LL;
 const int N = ;
 
 LL sum[N], g[N], p[N], top;
 LL f[N], y[N];
 
 inline double slope(int i, int j) {
     return ((double)(y[j] - y[i])) / (g[j] - g[i]);
 }
 
 inline int get(int i) {
     if(i == ) {
         return ;
     }
     double k = 2.0 * g[i];
     int l = , r = top, mid;
     while(l < r) {
         mid = (l + r) / ;
         //printf("%lf %lf \n", slope(p[mid], p[mid + 1]), k);
         if(slope(p[mid], p[mid + ]) < k) {
             l = mid + ;
         }
         else {
             r = mid;
         }
     }
     //printf("i = %d  r = %d  j = %d \n", i, r, p[r]);
     return p[r];
 }
 
 int main() {
     //freopen("in.in", "r", stdin);
     LL n, L;
     scanf("%lld%lld", &n, &L);
     L++;
     for(int i = ; i <= n; i++) {
         LL x;
         scanf("%lld", &x);
         sum[i] = sum[i - ] + x;
         g[i] = i + sum[i];
     }
     y[] = L * L;
     for(int i = ; i <= n; i++) {
         // f[i] = f[j] + (g[i] - g[j] - L) ^ 2
         int j = get(i);
 
         f[i] = f[j] + (g[i] - g[j] - L) * (g[i] - g[j] - L);
         y[i] = f[i] + (g[i] + L) * (g[i] + L);
         //printf("y[%d] = %d \n", i, y[i]);
 
         p[++top] = i;
         while(top >  && slope(p[top - ], p[top - ]) >= slope(p[top - ], p[top])) {
             p[top - ] = p[top];
             top--;
         }
     }
 
     /*for(int i = 1; i <= n; i++) {
         printf("%lld ", f[i]);
     }
     puts("");*/
     printf("%lld", f[n]);
     return ;
 }

AC代码

[update20181208]今天又考了一次玩具装箱，发现了一个问题.......怎么能把点的坐标直接带入到斜截式里面啊！！！！

只知道y - y0 = k(x - x0)，从来没听过y0 = kx0 + b啊啊啊！！！

关于上面那个的解释:(感谢某蒋姓巨佬为我讲解)

上面那个式子化简为2gi * gj + C = F(j)

考虑有某条直线过点（gj, F(j)），且方程为kx + b = y，其中k = 2gi

那么将点带入，可得：k * gj + b = F(j)

故上面那个等式即为直线的方程。

y - F(j) = 2gi(x - gj)

y - F(j) = 2gi * x - 2gi * gj

然后反正瞎搞一搞就行了啦我也不管了啊啊啊啊阿斜率优化好难啊啊我到底在写什么东西啊