bzoj2702[SDOI2012]走迷宫

题意：给你一个有向图,点数10000,边数1000000，SCC大小不超过100(按数据范围的写法只有第三部分数据满足这个条件,不过第二部分数据并没有出现大小大于100个点的SCC,我是用数组大小为100的代码以身试法的2333)从s出发随机走，问走到t的期望步数.

首先考虑inf的情况.如果从s出发可以走到一个无法走到t的点，比如这个数据：红色点为起点，绿色点为终点,那么有1/2的概率永远也走不到（在蓝色点停下）.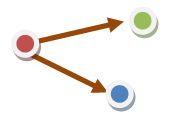

注意出现环的情况不一定是INF,因为在环上走无穷步的概率可能是无穷小。于是先缩点，把边反向找到所有不能到达t的SCC,如果从s出发有可能到达这样的一个SCC或s本身处于这样一个SCC，那么答案是INF。

接下来，我们把期望步数转化成期望经过的点数(显然经过的边数等于点数-1)，那么利用期望的线性性,只需要高斯消元求出每个点的期望经过次数再加起来。但是这个范围显然不能直接做。而SCC大小小于100，提醒我们可以对每个SCC分别进行高斯消元,然后考虑SCC之间的关系。思路类似USACO一道最短路题”道路与航线”,那道题是对每个SCC分别跑dijkstra。

具体的做法：记f[i]为点i的期望经过次数,g[i]为从另一个SCC走到点i的期望次数,因为我们按拓扑序处理每个SCC,所以在处理每个SCC的时候这个SCC中每个点的g[]值都已经求出来了.接下来对SCC中每个点列一个方程.对于点x,f[x]=g[x]+sigma(f[j]/outdeg[j]),j向x有一条有向边且j和x在同一个SCC，outdeg为出度。这里j可以等于x（有自环）,验证一下,这时候方程也是对的.解完这个SCC之后要用这个SCC里的点更新其他SCC的g[].注意边界g[s]=1,f[t]=1

然后码码码就好了。

#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
int n,m,s,t;
const int maxn=,maxm=;
//Graph Theory
struct edge{
  int to,next;
}lst1[maxm],lst2[maxm],lst3[maxm];int len1=,len2=,len3=;
int first1[maxn],first2[maxn],first3[maxn];
void addedge1(int a,int b){
  lst1[len1].to=b;lst1[len1].next=first1[a];
  first1[a]=len1++;
}
void addedge2(int a,int b){
  lst2[len2].to=b;lst2[len2].next=first2[a];
  first2[a]=len2++;
}
void addedge3(int a,int b){
  lst3[len3].to=b;lst3[len3].next=first3[a];
  first3[a]=len3++;
}
int outdeg[maxn];
int belong[maxn],tot,sz[maxn];
vector<int> scc[maxn];
int stk[maxn],top,dfn[maxn],low[maxn],T;
bool ins[maxn];
namespace Trajan{
  void dfs(int x){
    low[x]=dfn[x]=++T;
    stk[top++]=x;ins[x]=true;
    for(int pt=first1[x];pt;pt=lst1[pt].next){
      if(!dfn[lst1[pt].to]){
    dfs(lst1[pt].to);
    if(low[lst1[pt].to]<low[x])low[x]=low[lst1[pt].to];
      }else if(ins[lst1[pt].to]&&dfn[lst1[pt].to]<low[x])low[x]=dfn[lst1[pt].to];
    }
    if(dfn[x]==low[x]){
      ++tot;
      do{
    ins[stk[--top]]=false;
    belong[stk[top]]=tot;
    scc[tot].push_back(stk[top]);
    sz[tot]++;
      }while(stk[top]!=x);
    }
  }
  void tarjan(){
    for(int i=;i<=n;++i){
      if(!dfn[i])dfs(i);
    }
    for(int i=;i<=n;++i){
      for(int pt=first1[i];pt;pt=lst1[pt].next){
    if(belong[lst1[pt].to]!=belong[i]){
      addedge2(belong[lst1[pt].to],belong[i]);
      addedge3(belong[i],belong[lst1[pt].to]);
    }
      }
    }
  }
  bool reachfromend[maxn],mustreachend[maxn];
  void predfs(int x){
    reachfromend[x]=true;
    for(int pt=first2[x];pt;pt=lst2[pt].next){
      if(!reachfromend[lst2[pt].to]){
    predfs(lst2[pt].to);
      }
    }
  }
  bool checkdfs(int x){
    if(!reachfromend[x])return false;
    for(int pt=first3[x];pt;pt=lst3[pt].next){
      if(mustreachend[lst3[pt].to])continue;
      if(!checkdfs(lst3[pt].to))return false;
    }
    return mustreachend[x]=true;
  }
  bool check(){
    predfs(belong[t]);
    return checkdfs(belong[s]);
  }
};
double f[maxn],g[maxn];
int map[maxn];
namespace Work{
  bool done[maxn];
  double F[][];
  int rk;
  void Swap(int a,int b){
    for(int i=;i<=rk;++i)swap(F[a][i],F[b][i]);
  }
  void multplus(int a,int b,double times){
    for(int i=;i<=rk;++i)F[a][i]+=F[b][i]*times;
  }
  void Gauss(int n){
    rk=n;
    for(int i=;i<=n;++i){
      if(F[i][i]==){
    for(int j=i+;j<=n;++j){
      if(F[j][i]!=){
        Swap(i,j);break;
      }
    }
      }
      for(int j=i+;j<=n;++j)multplus(j,i,-F[j][i]/F[i][i]);
    }
    for(int i=n;i>=;--i){
      F[i][]/=F[i][i];
      for(int j=i-;j>=;--j){
    F[j][]-=F[j][i]*F[i][];
      }
    }
  }
  void build_equations(int x){
    for(int i=;i<=sz[x];++i){
      for(int j=;j<=sz[x];++j){
    F[i][j]=;
      }
    }
    for(int i=;i<sz[x];++i)F[i+][]=-g[scc[x][i]];
    for(int i=;i<=sz[x];++i){
      F[i][i]=-;map[scc[x][i-]]=i;
      if(scc[x][i-]==t)F[i][]=-;
    }
    for(int i=;i<sz[x];++i){
      if(scc[x][i]==t)continue;
      for(int pt=first1[scc[x][i]];pt;pt=lst1[pt].next){
    if(belong[lst1[pt].to]==x){
      if(lst1[pt].to==t)continue;
      F[map[lst1[pt].to]][i+]+=1.0/outdeg[scc[x][i]];
    }
      }
    }

  }
  void dfs(int x){
    for(int pt=first2[x];pt;pt=lst2[pt].next){
      if(!done[lst2[pt].to])dfs(lst2[pt].to);
    }
    build_equations(x);
    Gauss(sz[x]);
    for(int i=;i<sz[x];++i){
      f[scc[x][i]]=F[i+][];
    }
    for(int i=;i<sz[x];++i){
      for(int pt=first1[scc[x][i]];pt;pt=lst1[pt].next){
    if(belong[lst1[pt].to]!=x){
      g[lst1[pt].to]+=f[scc[x][i]]/outdeg[scc[x][i]];
    }
      }
    }
    done[x]=true;
  }
}
int main(){
  scanf("%d%d%d%d",&n,&m,&s,&t);
  int a,b;
  for(int i=;i<=m;++i){
    scanf("%d%d",&a,&b);addedge1(a,b);
    outdeg[a]++;
  }
  Trajan::tarjan();
  if(Trajan::check()){
    g[s]=;
    Work::dfs(belong[t]);
    double ans=;
    for(int i=;i<=n;++i){//printf("%.2f ",f[i]);
      ans+=f[i];
    }//ans:the expected number of points on the path from s to t
    printf("%.3f\n",ans-);
  }else{
    printf("INF\n");
  }
  return ;
}