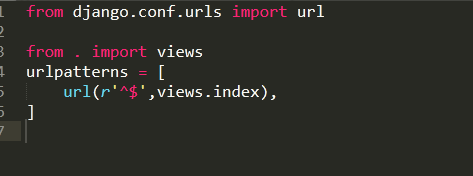
##另外一种url配置方法

首先要导入include

要包含blog目录下的urls.py(新建)的文件

从views连接到index

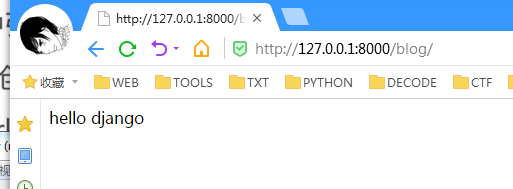
3.django学习的更多相关文章

  1. 今天主要推荐一下django学习的网址!

    前言:每个月忙碌的头20天后,在上班时间投入到django理论学习的过程中,花了差不多3天时间简单的研究了一下django,着实废了我不少脑细胞. 采用虫师前辈的一张图和话: 如果你把这过程梳理清晰了 ...

  2. Django 学习笔记之四 QuerySet常用方法

    QuerySet是一个可遍历结构,它本质上是一个给定的模型的对象列表,是有序的. 1.建立模型: 2.数据文件(test.txt) 3.文件数据入库(默认的sqlite3) 入库之前执行 数据库同步命 ...

  3. Django 学习笔记之三 数据库输入数据

    假设建立了django_blog项目,建立blog的app ,在models.py里面增加了Blog类,同步数据库,并且建立了对应的表.具体的参照Django 学习笔记之二的相关命令. 那么这篇主要介 ...

  4. Django学习系列之Form基础

     Django学习系列之Form基础 2015-05-15 07:14:57 标签:form django 原创作品,允许转载,转载时请务必以超链接形式标明文章 原始出处 .作者信息和本声明.否则将追 ...

  5. Django学习笔记（五）—— 表单

    疯狂的暑假学习之  Django学习笔记(五)-- 表单 參考:<The Django Book> 第7章 1. HttpRequest对象的信息 request.path         ...

  6. Django学习笔记（三）—— 型号 model

    疯狂暑期学习 Django学习笔记(三)-- 型号 model 參考:<The Django Book> 第5章 1.setting.py 配置 DATABASES = { 'defaul ...

  7. django学习之Model（二）

    继续(一)的内容: 1-跨文件的Models 在文件头部import进来,然后用ForeignKey关联上: from django.db import models from geography.m ...

  8. Python框架之Django学习

    当前标签: Django   Python框架之Django学习笔记(十四) 尛鱼 2014-10-12 13:55 阅读:173 评论:0     Python框架之Django学习笔记(十三) 尛 ...

  9. Django 学习笔记（二）

    Django 第一个 Hello World 项目 经过上一篇的安装,我们已经拥有了Django 框架 1.选择项目默认存放的地址 默认地址是C:\Users\Lee,也就是进入cmd控制台的地址,创 ...

  10. Django 学习笔记（五）模板标签

    关于Django模板标签官方网址https://docs.djangoproject.com/en/1.11/ref/templates/builtins/ 1.IF标签 Hello World/vi ...

随机推荐

  1. Js 常用字符串操作 API

    常用的一些字符串操作 API 整理 1.str.charAt(index).str.charCodeAt(index) - 返回指定位置的字符 / 字符编码(0~65535) index - 必须,表 ...

  2. JUC同步锁（五）

    根据锁的添加到Java中的时间,Java中的锁,可以分为"同步锁"和"JUC包中的锁". 一.同步锁--synchronized关键字 通过synchroniz ...

  3. codeforces-962-c

    题意:给你一个数,问从中删除某几位数字后重新组成的数字是否是某个数的平方: 解题思路:数据小,dfs直接搜,每位数只有两种选择,要或者不要 #include<iostream> #incl ...

  4. 搭建Hexo博客（二）－连接github

    没有github账号先需要创建账号,地址:https://github.com/join?source=header 有账号的看下面: 1.创建repo 创建一个repo,名称为yourname.gi ...

  5. kubernetes 创建系统用户来支持访问 dashboard

    Dashboard: 1.部署: 下载yaml文件  可以直接运行也可以下载下来kubectl apply -f https://raw.githubusercontent.com/kubernete ...

  6. Codeforces Round #433 Div. 1

    A:显然从大到小排序后贪心放在第一个能放的位置即可.并查集维护. #include<iostream> #include<cstdio> #include<cmath&g ...

  7. 戴尔服务器H330阵列卡取消磁盘阵列教程

    一:服务器开机看到ctrl+R提示,按ctrl+r进入阵列卡配置界面 二:按ctrl+N 转到PD Mgmt查看硬盘信息,确认硬盘状态:Ready 三:光标移到需配置硬盘上,按F2,选择 conver ...

  8. 51Nod1778 小Q的集合 【组合数】【Lucas定理】

    题目分析: 题解好高深...... 我给一个辣鸡做法算了,题解真的看不懂. 注意到方差恒为$0$,那么其实就是要我们求$\sum_{i=0}^{n}\binom{n}{i}(i^k-(n-i)^k)^ ...

  9. 用递归方法计算斐波那契数列（Recursion Fibonacci Sequence Python)

    先科普一下什么叫斐波那契数列,以下内容摘自百度百科: 斐波那契数列(Fibonacci sequence),又称黄金分割数列.因意大利数学家列昂纳多·斐波那契(Leonardoda Fibonacci ...

  10. day2 网络基础

    网路基础 网络OSI模型七层: 物理层: 定义特性:机械,电器,功能,过程: 定义接口标准:双绞线,光纤,同轴电缆: 相关协议:无: 数据链路层: 定义帧的开始结束,封装成帧,差错校验,透明传输(防止 ...