指数加权移动平均法（EWMA）

** 本文内容来自于吴恩达深度学习公开课

1、概述

　　加权移动平均法，是对观察值分别给予不同的权数，按不同权数求得移动平均值，并以最后的移动平均值为基础，确定预测值的方法。采用加权移动平均法，是因为观察期的近期观察值对预测值有较大影响，它更能反映近期变化的趋势。

　　指数移动加权平均法，是指各数值的加权系数随时间呈指数式递减，越靠近当前时刻的数值加权系数就越大。

　　指数移动加权平均较传统的平均法来说，一是不需要保存过去所有的数值；二是计算量显著减小。

2、算法理解

　　引入一个例子，例子为美国一年内每天的温度分布情况，具体如下图所示

　　　　

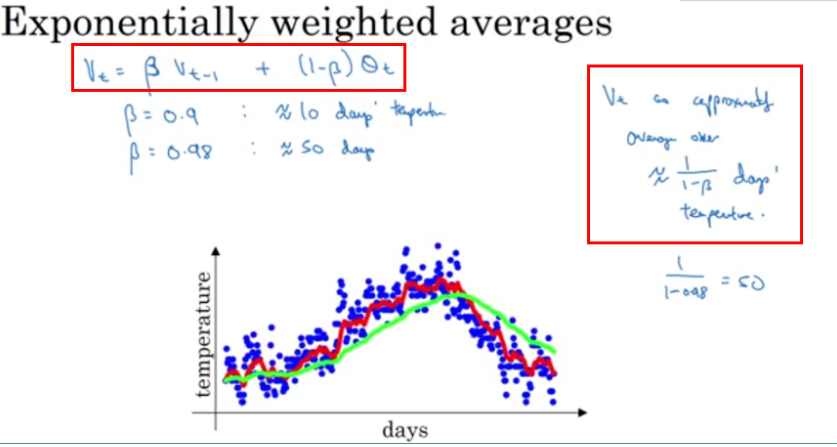
　　EWMA 的表达式如下：

　　　　$v_t = \beta v_{t-1} + (1 - \beta) \theta_t$

　　上式中 $ \theta_t$ 为时刻 $ t$ 的实际温度；系数 $\beta$ 表示加权下降的速率，其值越小下降的越快；$v_t$ 为 $t$ 时刻 EWMA 的值。

　　在上图中有两条不同颜色的线，分别对应着不同的 $\beta$ 值。

　　当 $\beta = 0.9$ 时，有 $v_t = 0.9 v_{t-1} + 0.1 \theta_t$ ，对应着图中的红线，此时虽然曲线有些波动，但总体能拟合真实数据

　　当 $\beta = 0.98$ 时，有 $v_t = 0.98 v_{t-1} + 0.02 \theta_t$ ，对应着图中的绿线，此时曲线较平，但却有所偏离真实数据

　　在 $t=0$ 时刻，一般初始化 $v_0 = 0$ ，对 EWMA 的表达式进行归纳可以将 $t$ 时刻的表达式写成：

　　　　$ v_t = (1-\beta)  (\theta_t + \beta\theta_{t-1}+ ... + \beta^{t-1}\theta_1) $

　　从上面式子中可以看出，数值的加权系数随着时间呈指数下降。在数学中一般会以 $\frac {1} {e}$ 来作为一个临界值，小于该值的加权系数的值不作考虑，接着来分析上面 $\beta = 0.9 $ 和 $\beta = 0.98$ 的情况。

　　当 $\beta = 0.9$ 时，$0.9^{10}$ 约等于 $\frac {1} {e}$ ，因此认为此时是近10个数值的加权平均。

　　当 $\beta = 0.98$ 时，$0.9^{50}$ 约等于 $\frac {1} {e}$，因此认为此时是近50个数值的加权平均。这种情况也正是移动加权平均的来源。

　　具体的分析如下图所示：

　　　　

3、偏差修正

　　在初始化 $ v_0 = 0$ 时实际上会存在一个问题。具体的如下图所示：

　　　　

　　从上图中可以看出有一条绿色和紫色的曲线，都是对应于 $\beta = 0.98$ 时的曲线。理想状况下应该是绿色的曲线，但当初始化 $v_0 = 0$ 时却会得到紫色的曲线，这是因为初始化的值太小，导致初期的数值都偏小，而随着时间的增长，初期的值的影响减小，紫色的曲线就慢慢和绿色的曲线重合。我们对公式做一些修改：

　　　　$ v_t = \frac {\beta {v_{t-1}}  + {(1 - \beta)} \theta_t} {1 - \beta^t} $　

　　当 $t$ 很小时，分母可以很好的放大当前的数值；当 $t$ 很大时，分母的数值趋于1，对当前数值几乎没有影响。

　　EWMA 主要是被应用在动量优化算法中，比如Adam算法中的一阶矩和二阶矩都采用了上面修改后的EWMA算法。