UVA116-Unidirectional TSP（动态规划基础）

Problem UVA116-Unidirectional TSP

Accept: 7167  Submit: 56893
Time Limit: 3000 mSec

Problem Description

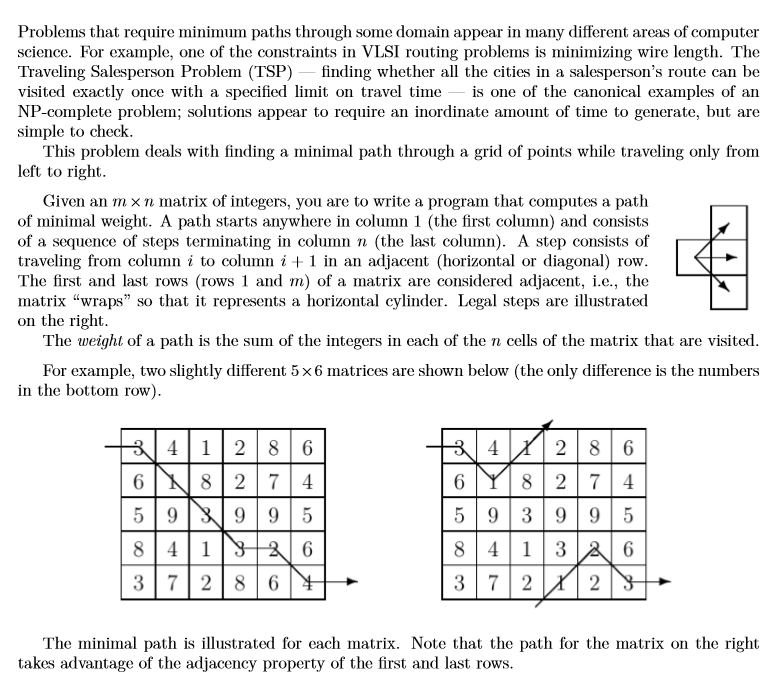
Input

The input consists of a sequence of matrix specifications. Each matrix specification consists of the row and column dimensions in that order on a line followed by m·n integers where m is the row dimension and n is the column dimension. The integers appear in the input in row major order, i.e., the first n integers constitute the first row of the matrix, the second n integers constitute the second row and so on. The integers on a line will be separated from other integers by one or more spaces. Note: integers are not restricted to being positive. There will be one or more matrix specifications in an input file. Input is terminated by end-of-file. Foreachspecificationthenumberofrowswillbebetween1and10inclusive; thenumberofcolumns will be between 1 and 100 inclusive. No path’s weight will exceed integer values representable using 30 bits.

 Output

Two lines should be output for each matrix specification in the input file, the first line represents a minimal-weightpath, andthesecondlineisthecostofaminimalpath. Thepathconsistsofasequence of n integers(separatedbyoneormorespaces)representingtherowsthatconstitutetheminimalpath. If there is more than one path of minimal weight the path that is lexicographically smallest should be output. Note: Lexicographically means the natural order on sequences induced by the order on their elements.

 

 Sample Input

5 6
3 4 1 2 8 6
6 1 8 2 7 4
5 9 3 9 9 5
8 4 1 3 2 6
3 7 2 8 6 4
5 6
3 4 1 2 8 6
6 1 8 2 7 4
5 9 3 9 9 5
8 4 1 3 2 6
3 7 2 1 2 3
2 2
9 10
9 10

 

Sample Output

1 2 3 4 4 5
16
1 2 1 5 4 5
11
1 1
19

题解：和数字三角形一样，水题。

 #include <bits/stdc++.h>

 using namespace std;

 const int maxn =  + , maxm =  + ;
 const int INF = 0x3f3f3f3f;

 int n, m;
 int val[maxm][maxn], dp[maxm][maxn];
 int Next[maxm][maxn];

 int read() {
     int q = , f = ; char ch = ' ';
     while (ch<'' || ch>'') {
         if (ch == '-') f = -;
         ch = getchar();
     }
     while ('' <= ch && ch <= '') {
         q = q *  + ch - '';
         ch = getchar();
     }
     return q * f;
 }

 int main()
 {
     //freopen("input.txt", "r", stdin);
     while (~scanf("%d%d", &m, &n)) {
         for (int i = ; i < m; i++) {
             for (int j = ; j < n; j++) {
                 val[i][j] = read();
             }
         }
         //memset(dp, INF, sizeof(dp));
         int ans = INF, first = -;

         for (int j = n - ; j >= ; j--) {
             for (int i = ; i < m; i++) {
                 if (j == n - ) {
                     dp[i][j] = val[i][j];
                 }
                 else {
                     int row[] = { (i -  + m) % m,i,(i + ) % m };
                     sort(row, row + );
                     dp[i][j] = INF;
                     for (int k = ; k < ; k++) {
                         if (dp[i][j] > dp[row[k]][j + ] + val[i][j]) {
                             dp[i][j] = dp[row[k]][j + ] + val[i][j];
                             Next[i][j] = row[k];
                         }
                     }
                 }
                 if (j ==  && dp[i][j] < ans) {
                     ans = dp[i][j];
                     first = i;
                 }
             }
         }

         printf("%d", first + );
         for (int i = Next[first][], j = ; j < n; i = Next[i][j], j++) {
             printf(" %d", i + );
         }
         printf("\n%d\n", ans);
     }
     return ;
 }