多项式乘法(FFT)学习笔记

------------------------------------------
本文只探讨多项式乘法(FFT)在信息学中的应用
如有错误或不明欢迎指出或提问，在此不胜感激

多项式

1.系数表示法
     一般应用最广泛的表示方式
     用A(x)表示一个x-1次多项式，a[i]为$ x^i$的系数，则A(x)=$ \sum_0^{n-1}$ a[i] * $ x^i$

仅利用这种方式求多项式乘法复杂度为O($ n^2$)，不够优秀
2.点值表示法
     将n个互不相同的值$ x_0$...$ x_{n-1}$带入多项式，可以得到
     对于一个n-1次多项式，可以被n个点所唯一对应.
     因而对于A(x)*B(x),只需要得知A的2n个点值和对应B的点值即可O(n)求出多项式的乘积
     然而得知这些点值的复杂度依然在平方级别，达不到要求

考虑优化
先引一些要用到的名词

复数
复数即为表示成a+bi的数，其中i为-1的平方根
表示：
     可以通过平面直角坐标系上的一条向量(0,0)到(x,y)表示x+yi
     其中x轴为实数轴，y轴为虚数轴
运算：
     复数运算符合四则运算，即：
     (a+bi) + (c+di) = (a+c) + (b+d)i;
     (a+bi) * (c+di) = ac + adi + bci + bd$ i^2$ =(ac - bd) + (bc + ad)i
几何意义：
     定义模长为向量长度，幅角为从x轴正半轴逆时针转动到向量的角
     复数相加等同于向量加法
     复数相乘，模长相乘，幅角相加
//建议complex类手写，速度优于STL

单位根
以下默认n为$ 2^x$ 且x为非负整数
在复数平面，以原点为圆心，以1为半径作圆
以x轴正半轴到其与原交点(0,0)到(1,0)的这条向量为起点n等分圆，圆心到每个n等分点的向量均称为n次单位根
对于一个单位根，其标号为幅角/(360°/n)，特别的，(0,0)到(1,0)的向量标号为0
以下用$ w_n^k$ 表示标号为k的n次单位根

单位根的性质
     1. $ w_n^k$ = cos($ \frac{2π}{n}$)k + sin($ \frac{2π}{n}$)ki
     证明:欧拉公式

2. $ w_n^k$ = $ w_{2n}^{2k}$
     证明:带入式1，等价于分子分母同乘2,

3. $ w_n^k$ * $ w_n^k$=$ w_n^{2k}$
     证明:根据（复数相乘，模长相乘，幅角相加）
     又因为模长均为1，所以相当于只把转动角度乘2

4. $ w_n^{k+\frac{n}{2}}$ = -$ w_n^k$
     证明:$ w_n^{k+\frac{n}{2}}$相当于在$ w_n^k$的基础上逆时针方向再旋转180° （复数相乘，模长相乘，幅角相加）
     因而等价于取负

进入正题
递归完成快速傅里叶变换

设多项式A(x)的系数为$ a_0$...$ a_{n-1}$
则

A(x)=$ a_0$ + $ a_1$*x + $ a_2$*$ x^2$ + $ a_3$*$ x^3$ + $ a_4$*$ x^4$ + ... + $ a_{n-2}$*$ x^{n-2}$ + $ a_{n-1}$*$ x^{n-1}$

按下标奇偶性分成两组，在这里设
        A0(x) = $ a_0$ + $ a_2$ * $ x$ + $ a_4$ * $ x^2$ + ... + $ a_{n-2}$ * $ x^\frac{n-2}{2}$
        A1(x) = $ a_1$ + $ a_3$ * $ x$ + $ a_5$ * $ x^2$ + ... + $ a_{n-1}$ * $ x^\frac{n-2}{2}$

显然得到A(x) = A0($ x^2$) + xA1($ x^2$)
我们代单位根$ w_n^k$(0<=k<$ \frac{n}{2}$)入式得

A($ w_n^k$)=A0($ w_n^{2k}$)+$ w_n^k$A1($ w_n^{2k}$)//性质3

同理代$ w_n^{k+\frac{n}{2}}$入式得

A($ w_n^{k+\frac{n}{2}}$)=A0($ w_n^{2k+n}$)+$ w_n^{k+\frac{n}{2}}$A1($ w_n^{2k+n}$)
 = A0($ w_n^{2k}$) - $ w_n^k$ * A1($ w_n^{2k}$)//性质4&&$ w_n^n$=1

容易发现上下两式只有常数项的符号不同
因而只需求前一半即可得到后一半
递归形式程序结构：
对于长度为n的A(x)
分割成长度为$ \frac{n}{2}$的A0(x)和A1(x)
求A0(x)和A1(x)
通过A0(x)和A1(x)计算带入$ w_n^k$(0<=k<$ \frac{n}{2}$)时的值
变号计算代$ w_n^{k+\frac{n}{2}}$入式的值

我们可以用数组A[i]表示某一多项式(不一定是初始多项式)代入$ w_n^i$}时的值
由于许多奥妙重重的性质，我们不需要对于每个多项式都维护整个数组A，只需要维护它需要返回的值即可
绘图可得，当某一多项式递归到只有一项的时候，要返回的一定只是$ w_n^0$(1)，即直接返回原多项式该项系数即可
递归代码：

void FFT(const int lim,cp *A){//cp即为complex类型,lim为2^n的整型if(lim==)return;//直接返回对应常数项
    cp A0[lim>>],A1[lim>>];
    for(rt i=;i<lim;i+=)A0[i>>]=A[i],A1[i>>]=A[i+];
    FFT(lim>>,A0,fla);FFT(lim>>,A1,fla);//递归求解
    cp w={cos(PI*2.0/lim),sin(PI*2.0/lim)},k={,};//w为1号单位根
    for(rt i=;i<lim>>;i++,k=k*w){//k即为第i个单位根

        A[i]=A0[i]+k*A1[i];//A0，A1数组中的i号本相当于A数组中的2i号，乘2再除2后相当于没有
        A[i+(lim>>)]=A0[i]-k*A1[i];
    }
}

逆变换
以上求得的均为点值表示法的结果
需要将其转回系数表示法
实际操作相当于再进行FFT时单位根逆向(顺时针)计算
递归全代码

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define rt register int
#define ll long long
using namespace std;
ll read(){
    ll x = ; int zf = ; char ch;
    while (ch != '-' && (ch < '' || ch > '')) ch = getchar();
    if (ch == '-') zf = -, ch = getchar();
    while (ch >= '' && ch <= '') x = x *  + ch - '', ch = getchar(); return x * zf;
}
void write(ll y){
    if (y < ) putchar('-'), y = -y;
    if (y > ) write(y / );
    putchar(y %  + '');
}
int i,j,k,m,n,x,y,z,cnt,all,num;
struct cp{
    double x,y;
}a[],b[];
inline cp operator +(const cp x,const cp y){return {x.x + y.x, x.y + y.y};}
inline cp operator *(const cp x,const cp y){return {x.x * y.x - x.y * y.y, x.x * y.y + x.y * y.x};}
inline cp operator -(const cp x,const cp y){return {x.x - y.x, x.y - y.y};}
const double PI=acos(-1.0);
void FFT(const int lim,cp *A,const int fla){//fla为-1表示逆变换
    if(lim==)return;cp A1[lim>>],A2[lim>>];
    for(rt i=;i<lim;i+=)A1[i>>]=A[i],A2[i>>]=A[i+];
    FFT(lim>>,A1,fla);FFT(lim>>,A2,fla);
    cp w={cos(PI*2.0/lim),sin(PI*2.0/lim)*fla},k={,};
    for(rt i=;i<lim>>;i++,k=k*w){
        A[i]=A1[i]+k*A2[i];
        A[i+(lim>>)]=A1[i]-k*A2[i];
    }
}
int main(){
    n=read();m=read();
    for(rt i=;i<=n;i++)a[i].x=read(),a[i].y=;
    for(rt i=;i<=m;i++)b[i].x=read(),b[i].y=;
    int limit=;while(limit<=n+m)limit<<=;//将多项式长度凑到2^n
    FFT(limit,a,);FFT(limit,b,);
    for(rt i=;i<=limit;i++)a[i]=a[i]*b[i];//a为点值表示的多项式
    FFT(limit,a,-);//逆变换
    for(rt i=;i<=n+m;i++)write(a[i].x/limit+0.5),putchar(' ');
    //因为有limit个单位根因而答案需要除limit，0.5是四舍五入
    return ;
}

问题：常数巨大
解决方案：改成非递归(迭代)形式
观察下图

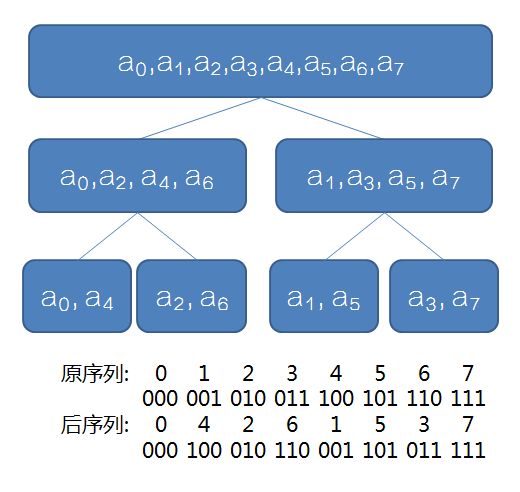
发现底层序列的值相当于原序列的值的二进制反转
因而我们可以预处理底层的值然后迭代向上推

如何预处理
1.x为偶数
     x=(x>>1)<<1;
     在反转序列中reverse[x]=reverse[x>>1]>>1;
2.x为奇数
     相当于x-1的结果再在最高位补1

这样我们得到底层结果之后，一层一层向上迭代合并即可
迭代代码：

#include<ctime>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define rt register int
#define ll long long
using namespace std;
inline ll read(){
    ll x = ; char zf = ; char ch = getchar();
    while (ch != '-' && !isdigit(ch)) ch = getchar();
    if (ch == '-') zf = -, ch = getchar();
    while (isdigit(ch)) x = x *  + ch - '', ch = getchar(); return x * zf;
}
void write(ll y){if(y<)putchar('-'),y=-y;if(y>)write(y/);putchar(y%+);}
void writeln(const ll y){write(y);putchar('\n');}
int i,j,k,m,n,x,y,z,cnt,lim;
struct cp{
    double x,y;
    cp operator +(const cp s)const{
        return (cp){x+s.x,y+s.y};
    }
    cp operator -(const cp s)const{
        return (cp){x-s.x,y-s.y};
    }
    cp operator *(const cp s)const{
        return (cp){x*s.x-y*s.y,x*s.y+y*s.x};
    }
}a[],b[];
int R[];
const double PI=acos(-1.0);
void FFT(cp *A,int fla){
    for(rt i=;i<lim;i++)if(i>R[i])swap(A[i],A[R[i]]);
    for(rt i=;i<lim;i<<=){
        cp w={cos(PI/i),fla*sin(PI/i)};
        for(rt j=;j<lim;j+=i<<){
            cp K={,};
            for(rt k=;k<i;k++,K=K*w){
                cp x=A[j+k],y=K*A[i+j+k];
                A[j+k]=x+y,A[i+j+k]=x-y;
            }
        }
    }
}
int main(){
    n=read();m=read();lim=;
    for(rt i=;i<=n;i++)a[i].x=read();
    for(rt i=;i<=m;i++)b[i].x=read();
    while(lim<=n+m)lim<<=;
    for(rt i=;i<lim;i++)R[i]=(R[i>>]>>)|((i&)*lim>>);
    FFT(a,);FFT(b,);
    for(rt i=;i<lim;i++)a[i]=a[i]*b[i];
    FFT(a,-);
    for(rt i=;i<=n+m;i++)write(a[i].x/lim+0.5),putchar(' ');
    return ;
}