Lineage逻辑回归分类算法
Lineage逻辑回归分类算法
线性回归和逻辑回归参考文章:
http://blog.csdn.net/viewcode/article/details/8794401
http://www.cnblogs.com/jerrylead/archive/2011/03/05/1971867.html
1、概述
Lineage逻辑回归是一种简单而又效果不错的分类算法
什么是回归:比如说我们有两类数据,各有50十个点组成,当我门把这些点画出来,会有一条线区分这两组数据,我们拟合出这个曲线(因为很有可能是非线性),就是回归。我们通过大量的数据找出这条线,并拟合出这条线的表达式,再有新数据,我们就以这条线为区分来实现分类。
学习过程:
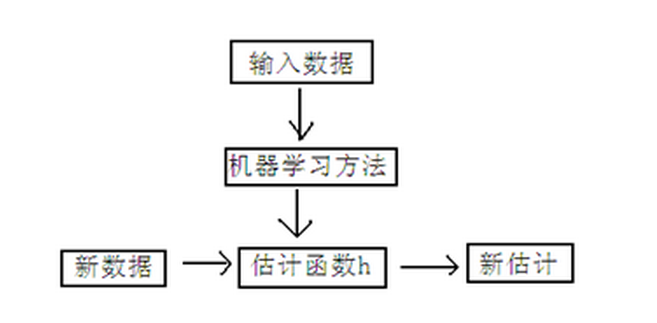
下图是一个数据集的两组数据,中间有一条区分两组数据的线。
显然,只有这种线性可分的数据分布才适合用线性回归
逻辑回归的模型 是一个非线性模型,sigmoid函数,又称逻辑回归函数。但是它本质上又是一个线性回归模型,因为除去sigmoid映射函数关系,其他的步骤,算法都是线性回归的。可以说,逻辑回归,都是以线性回归为理论支持的。
只不过,线性模型,无法做到sigmoid的非线性形式,sigmoid可以轻松处理0/1分类问题。
2、算法思想
Lineage回归分类算法就是将线性回归应用在分类场景中
在该场景中,计算结果是要得到对样本数据的分类标签,而不是得到那条回归直线
2.1、算法图示
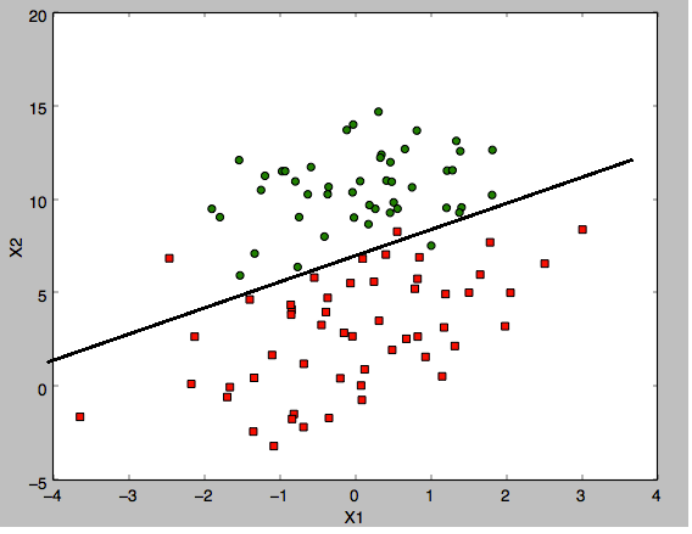
1) 算法目标()?
大白话:计算各点的y值到拟合线的垂直距离,如果
距离>0, 分为类A
距离<0, 分为类B
2) 如何得到拟合线呢?
大白话:只能先假设,因为线或面的函数都可以表达成
y(拟合)=w1*x1 + w2*x2 + w3*x3 + ...
其中的w是待定参数
而x是数据的各维度特征值
因而上述问题就变成了 样本y(x) - y(拟合) >0 ? A : B
3) 如何求解出一套最优的w参数呢?
基本思路:代入“先验数据”来逆推求解
但针对不等式求解参数极其困难
通用的解决办法,将对不等式的求解做一个转换:
- 将“样本y(x) - y(拟合) ”的差值压缩到一个0~1的小区间,
- 然后代入大量的样本特征值,从而得到一系列的输出结果;
- 再将这些输出结果跟样本的先验类别比较,并根据比较情况来调整拟合线的参数值,从而是拟合线的参数逼近最优
从而将问题转化为逼近求解的典型数学问题
2.2、sigmoid函数
上述算法思路中,通常使用sigmoid函数作为转换函数
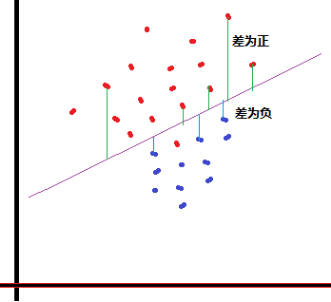
函数表达式:
注:此处的x是向量
函数曲线:
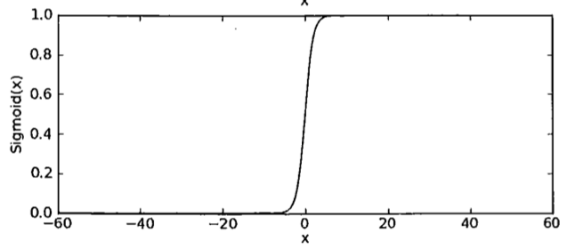
之所以使用sigmoid函数,就是让样本点经过运算后得到的结果限制在0~1之间,压缩数据的巨幅震荡,从而方便得到样本点的分类标签(分类以sigmoid函数的计算结果是否大于0.5为依据)
3、算法实现分析
3.1、实现思路
算法思想的数学表述:
把数据集的特征值设为x1,x2,x3......
求出它们的回归系数wi
设z=w1*x1+w2*x2..... ,然后将z值代入sigmoid函数并判断结果,即可得到分类标签
问题在于如何得到一组合适的参数wi?
通过解析的途径很难求解,而通过迭代的方法可以比较便捷地找到最优解
简单来说,就是不断用样本特征值代入算式,计算出结果后跟其实际标签进行比较,根据差值来修正参数,然后再代入新的样本值计算,循环往复,直到无需修正或已到达预设的迭代次数
注:此过程用梯度上升法来实现。
3.2、梯度上升算法
通俗解释:通过小步前进——》调整方向——》继续小步前进——》最终逼近最优解
梯度上升是指找到函数增长的方向。在具体实现的过程中,不停地迭代运算直到w的值几乎不再变化为止。
如图所示:
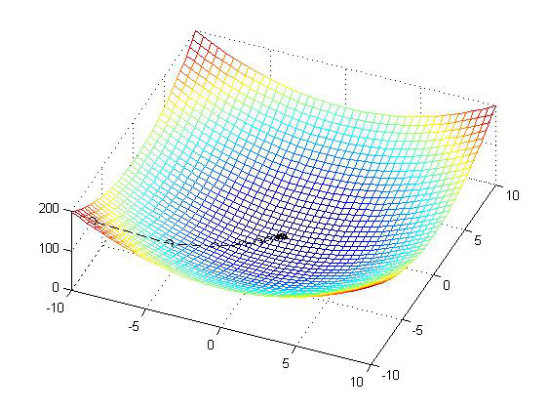
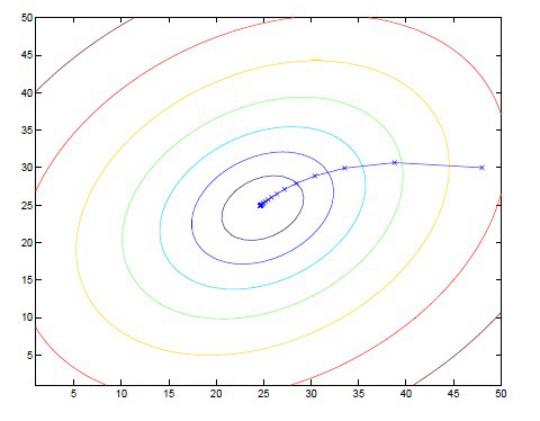
Lineage逻辑回归分类算法的更多相关文章
- Logistic回归分类算法原理分析与代码实现
前言 本文将介绍机器学习分类算法中的Logistic回归分类算法并给出伪代码,Python代码实现. (说明:从本文开始,将接触到最优化算法相关的学习.旨在将这些最优化的算法用于训练出一个非线性的函数 ...
- 用Python开始机器学习(7:逻辑回归分类) --好!!
from : http://blog.csdn.net/lsldd/article/details/41551797 在本系列文章中提到过用Python开始机器学习(3:数据拟合与广义线性回归)中提到 ...
- 第七篇:Logistic回归分类算法原理分析与代码实现
前言 本文将介绍机器学习分类算法中的Logistic回归分类算法并给出伪代码,Python代码实现. (说明:从本文开始,将接触到最优化算法相关的学习.旨在将这些最优化的算法用于训练出一个非线性的函数 ...
- 逻辑回归(分类问题)(Logistic Regression、罗杰斯特回归)
逻辑回归:问题只有两项,即{0, 1}.一般而言,回归问题是连续模型,不用在分类问题上,且噪声较大,但如果非要引入,那么采用逻辑回归模型. 对于一般训练集: 参数系统为: 逻辑回归模型为: ...
- 机器学习(1)- 概述&线性回归&逻辑回归&正则化
根据Andrew Ng在斯坦福的<机器学习>视频做笔记,已经通过李航<统计学习方法>获得的知识不赘述,仅列出提纲. 1 初识机器学习 1.1 监督学习(x,y) 分类(输出y是 ...
- stanford coursera 机器学习编程作业 exercise 3(逻辑回归实现多分类问题)
本作业使用逻辑回归(logistic regression)和神经网络(neural networks)识别手写的阿拉伯数字(0-9) 关于逻辑回归的一个编程练习,可参考:http://www.cnb ...
- 【原】Coursera—Andrew Ng机器学习—编程作业 Programming Exercise 3—多分类逻辑回归和神经网络
作业说明 Exercise 3,Week 4,使用Octave实现图片中手写数字 0-9 的识别,采用两种方式(1)多分类逻辑回归(2)多分类神经网络.对比结果. (1)多分类逻辑回归:实现 lrCo ...
- 逻辑回归LR
逻辑回归算法相信很多人都很熟悉,也算是我比较熟悉的算法之一了,毕业论文当时的项目就是用的这个算法.这个算法可能不想随机森林.SVM.神经网络.GBDT等分类算法那么复杂那么高深的样子,可是绝对不能小看 ...
- DeepLearning之路(一)逻辑回归
逻辑回归 1. 总述 逻辑回归来源于回归分析,用来解决分类问题,即预测值变为较少数量的离散值. 2. 基本概念 回归分析(Regression Analysis):存在一堆观测资料,希望获得数据内 ...
随机推荐
- Javaweb学习笔记——(四)——————JavaScript基础&DOM目录
1.案例一:在末尾添加节点 第一个:获取到ul标签 第二部:创建li标签 document.createElement("标签名称")方法 第三步:创建文本 document.cr ...
- MyBatis第一个案例-----永远的HelloWorld 含所有代码
1.创建表emp CREATE DATABASE mybatis; USE mybatis; CREATE TABLE emp( id INT(11) PRIMARY KEY AUTO_INCREME ...
- 20155331 2016-2017-2 《Java程序设计》第七周学习总结
20155331 2016-2017-2 <Java程序设计>第七周学习总结 教材学习内容总结 一.认识Lambda语法 1.Lambda语法概览 Arrays的sort()方法可以用来排 ...
- yolov3实践(一)
很多博友看了我的第一篇博客yolo类检测算法解析——yolo v3,对其有了一定的认识和了解,但是并没有贴出代码和运行效果,略显苍白.因此在把篇博客理论的基础上,造就了第一篇实践文章,也就是本文.只要 ...
- hdp3: regionserver running as process 3170. Stop it first.
1 启动hbase报错 hdp3: regionserver running as process 3170. Stop it first. 2 始终没有发现错误日志 3 jps没有发现hbase的r ...
- Python中os.system和os.popen区别
Python调用Shell,有两种方法:os.system(cmd)或os.popen(cmd)脚本执行过程中的输出内容.实际使用时视需求情况而选择. 两者的区别是: os.system(cmd)的返 ...
- javaScript中自定义sort中的比较函数,用于比较字符串长度,数值大小
, 1.2, 'bb', 'cc']; var len = arr.length; // for (var i = 0; i < len; i++) { // alert(arr + &qu ...
- centos 报错 “Job for iptables.service failed because the control process exited with error code.”的解决办法
原因:因为centos7默认的防火墙是firewalld防火墙,不是使用iptables,因此需要先关闭firewalld服务,或者干脆使用默认的firewalld防火墙. 操作步骤: 关闭防火墙 1 ...
- 深入浅出 JavaScript 关键词 -- this
深入浅出 JavaScript 关键词 -- this 要说 JavaScript 这门语言最容易让人困惑的知识点,this 关键词肯定算一个.JavaScript 语言面世多年,一直在进化完善,现在 ...
- CF126B
CF126B Password 题意: 给出一个字符串 H,找一个最长的字符串 h,使得它既作为前缀出现过.又作为后缀出现过.还作为中间的子串出现过. 解法: 沿着 $ next_n $ 枚举字符串, ...
