Xmind settings lower
Xmind settings lower
1● setting

2● options

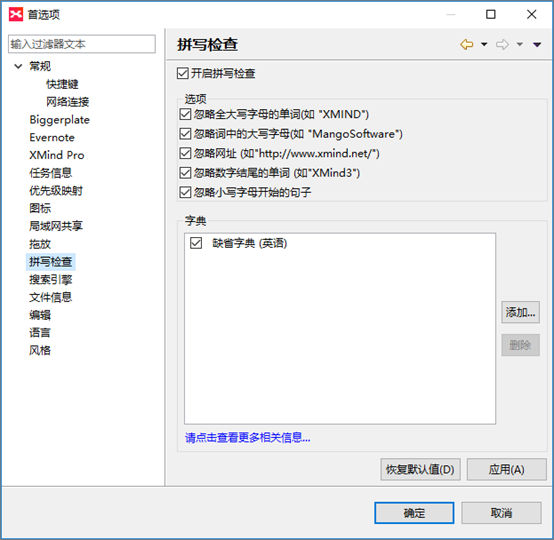
3● fast short keys

|
快捷键(Windows) |
快捷键(Mac) |
描述 |
|
Ctrl+N |
Command+N |
建立新工作簿 |
|
Ctrl+O |
Command+O |
开启工作簿 |
|
Ctrl+S |
Command+S |
储存目前工作簿 |
|
Ctrl+Shift+S |
Command+Shift+S |
储存全部工作簿 |
|
Ctrl+W |
Command+W |
关闭目前工作簿 |
|
Ctrl+Shift+W |
Command+Shift+W |
关闭全部工作簿 |
|
Ctrl+P |
Command+P |
列印 |
|
Ctrl+Z |
Command+Z |
复原 |
|
Ctrl+Y |
Command+Y |
重做 |
|
Ctrl+X |
Command+X |
剪切 |
|
Ctrl+C |
Command+C |
复制 |
|
Ctrl+V |
Command+V |
贴上 |
|
Delete |
Delete |
删除 |
|
Ctrl+Home |
Command+Home |
返回中心主题 |
|
Ctrl+A |
Command+A |
选择全部主题 |
|
Ctrl+Shift+A |
Command+Shift+A |
选择同层级主题 |
|
Ctrl+Alt+A |
Command+Alt+A |
选择子主题 |
|
Ctrl+F |
Command+F |
寻找/取代 |
|
Ctrl++ |
Command++ |
放大 |
|
Ctrl+- |
Command+- |
缩小 |
|
Ctrl+= |
Command+= |
正常大小 |
|
Ctrl+] |
Command+] |
插入摘要 |
|
Alt+Enter |
Alt+Enter |
属性内容内容 |
|
Enter |
Enter |
插入主题 |
|
Tab |
Tab |
插入子主题 |
|
Shift+Enter |
Shift+Enter |
在目前主题前插入主题 |
|
Ctrl+Enter |
Command+Enter |
插入目前主题父主题 |
|
Ctrl+Shift+L |
Command+Shift+L |
快捷键助手 |
|
Ctrl+I |
Ctrl+I |
插入图片 |
|
Ctrl+Shift+H |
Command+Shift+H |
插入超链接 |
|
Ctrl+B |
Command+B |
添加外框 |
|
Ctrl+L |
Command+L |
添加关联 |
|
F2 |
F2 |
编辑主题 |
|
F3 |
F3 |
添加/编辑标签 |
|
F4 |
F4 |
添加/编辑备注 |
|
F5 |
F5 |
简报演示 |
|
F6 |
F6 |
下钻 |
|
Shift+F6 |
Shift+F6 |
上钻 |
|
F7 |
F7 |
智慧截取图面 |
|
+ |
+ |
展开目前分支 |
|
- |
- |
收缩目前分支 |
|
* |
* |
展开所有分支 |
|
/ |
/ |
收缩所有分支 |
|
Alt+Up |
Alt+Up |
向前移动 |
|
Alt+Down |
Alt+Down |
向后移动 |
|
Ctrl+T |
Command+T |
建立新心智图 |
|
Ctrl+1,2,3,4,5,6 |
Command+1,2,3,4,5,6 |
快速添加优先等级图标 |
|
Esc |
Esc |
关闭跳出的备注对话框 / 取消截图 |
|
Ctrl+滑鼠滚轮 |
Command+滑鼠滚轮 |
放大缩小目前的画面 |
Xmind settings lower的更多相关文章
- django settings最佳配置
# encoding=utf-8 import os import socket SITE_ID = 1 # 项目的根目录 # 简化后面的操作 PROJECT_ROOT = os.path.dirna ...
- ubuntu 软件安装配置使用总结(由xmind:Depends:java8-runtime but is not installed引出)
ubuntu 软件安装总结(由xmind:Depends:java8-runtime but is not installed引出) 不知道抽什么风,这几天PC上又用起了linux操作系统.其实之前断 ...
- XSplit Quality, VBV-Buffer, VBV-Maxrate and Preset Settings
XSplit uses the x264 encoder, so let's start off by saying that parameters mentioned in the title, w ...
- Player Settings 导出设置
Player Settings is where you define various parameters (platform specific) for the final game that y ...
- Django -- settings 详解
Django settings详解 1.基础 DJANGO_SETTING_MODULE环境变量:让settings模块被包含到python可以找到的目录下,开发情况下不需要,我们通常会在当前文件夹运 ...
- Django -- settings 详解(转)
Django -- settings 详解 Django settings详解 1.基础 DJANGO_SETTING_MODULE环境变量:让settings模块被包含到python可以找到的目 ...
- unity 质量设置 Quality Settings
Unity allows you to set the level of graphical quality it will attempt to render. Generally speaking ...
- 播放器设置 Player Settings
原地址:http://game.ceeger.com/Manual/class-PlayerSettings.html#Android Player Settings is where you def ...
- xmind 8 readme
xmind 8 readme README LICENSE XMind 3 is dual licensed under 2 open source licenses: the Ecl ...
随机推荐
- JaveWeb 公司项目(3)----- 通过Thrift端口获取数据库数据
前面两篇博客的内容主要是界面搭建的过程,随着界面搭建工作的完成,网页端需要加入数据,原先的B/S架构中C#通过Thrift接口获取数据,所以在网页端也沿用这个设计 首先,新建一个Maven下的Web项 ...
- lattice 作图 举例
library(lattice) Depth <- equal.count(quakes$depth, number=8, overlap=.1)xyplot(lat ~ long | Dept ...
- AD中设置PCB线间距
Design->Rules->Electrical->Clearance->Clearance
- (转)stm32硬件IIC
cube与I2C:https://www.cnblogs.com/121792730applllo/p/5044920.html I2C官网:https://www.i2c-bus.org/stand ...
- v891 安卓平板的root
看了 油管的视频,标题:Onda V891 - Root Android 4.4.4 (Kit Kat) 2)下载工具,照着做就行了. 3)root完之后,安装 [钛备份](TitaniumBacku ...
- 数据结构(C语言版)-第4章 串、数组和广义表
补充:C语言中常用的串运算 调用标准库函数 #include<string.h> 串比较,strcmp(char s1,char s2) 串复制,strcpy(char to,char f ...
- MySql常用函数 --MySql
1.目标 MySQL数据库中提供了很丰富的函数.MySQL函数包括数学函数.字符串函数.日期和时间函数.条件判断函数.系统信息函数.加密函数.格式化函数等.通过这些函数,可以简化用户的操作.例如,字符 ...
- python paramiko自动登录网络设备抓取配置信息
ssh = paramiko.SSHClient()ssh.set_missing_host_key_policy(paramiko.AutoAddPolicy())ssh.connect(hostn ...
- java开学第一周测试代码
Account.java /* 信1705-3 20173612 陈阳阳 */package ATM; public class Account { private String accountID ...
- android ------ Emulator: error: x86 emulation currently requires hardware acceleration
我创建 Android 模拟器,运行项目时出现了一个这样的错误: 如下: emulator ERROR:x86 emulation currently requires hardware accele ...
