后缀自动机 && 题目

因为明天要讲解后缀自动机了，所以只能抱抱佛脚，临时做做题目。其实很久以前看过，但是不太懂，看的是clj的原文，不太懂。现在只能临时看看是怎么弄的，应付下。

------------------------------------------------------------------------------------------------------------------------------

1、自动机A为后缀自动机，A(sub) = true当且仅当sub是str的后缀。

2、一个较差的和后缀自动机有相同功能的东西是trie，把所有后缀都insert进去trie里面，但是空间&&时间复杂度O（N^2），不行。

3、有一个空间和时间复杂度都是O(N)的，就是：以ACADD为例子

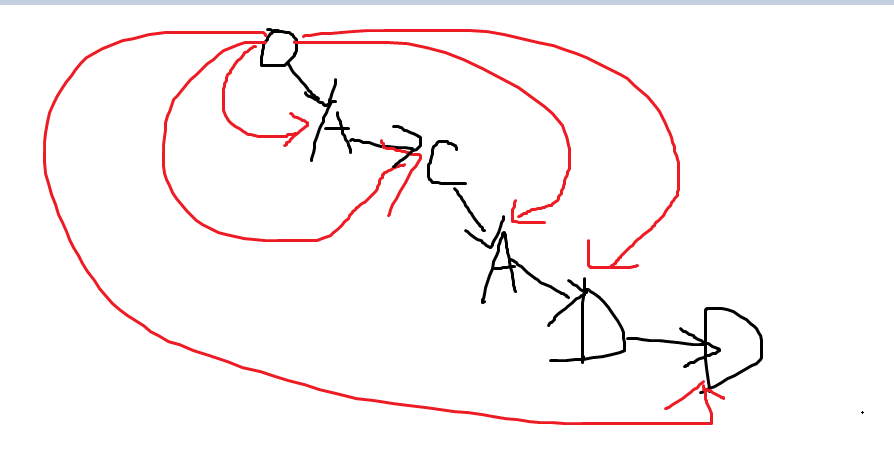
也就是向每个字符都添加一条边，然后顺着这条边遍历，就能找到所有后缀。也能保存所有子串。

但是查找复杂度O（N^2）

注意到连接去字符'A'的边是有两条的，也就是这个图只能用邻接表来存，不能像trie这样用pNext[26]这样存，所以查找是O(N^2)

SAM就是为了解决了这样的问题而诞生的，也就是每一种字母边，只能存在一条。

后缀自动机是一个基于trie的字符串有向图，时间和空间复杂度均为O（N）

构造过程：

假设现在已经建立好前t个字符的后缀自动机，现在要增加一个字符x，使得其变成tx的后缀自动机。

每个节点保存的信息如下：

    int cnt; // cnt表示后缀自动机中从root走到它最多需要多少步
    int id; //表示它是第几个后缀自动机节点，指向了它，但是不知道是第几个，用id判断
    int pos; //pos表示它在原串中的位置。

上面保存的信息都比较易懂，关键看看pNext[N]和fa，pNext[N]其实就是和字典树的26枚指针一样，只是为了O（1）判断是否存在这种字母的边。fa，指向的是一个能接受后缀的节点。什么叫能接受后缀的节点？比如我现在要建立"sazaa"的sam，一开始建立了's'的，如下图

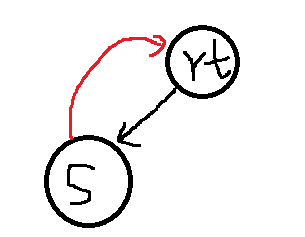
红色的是fa边，然后现在新来一个字符'a'，要使得其变成"sa"的sam，sam有什么特征呢，就是对于每一个"sa"的后缀，他都要能够识别。

那么，现在的末尾节点s，是肯定能够接受后缀的，然后爬fa边，去到root，root也和'a'连一条边，因为我也需要识别'a'这个后缀。

所以总的来说，fa边是为了寻找可以添加后缀节点的节点，使得其能识别当前建立的前缀串的所有后缀的。

在建立的时候，会遇到一种情况就是重边，我们用下标来判断是否能识别这个字符，那么很明显不能连接两条边。

但是建立的过程中，我们确实需要两条边。

比如建立到第四个"a"的时候，由于root-->a(2)已经有边，所以就不能连接root--->a(4)

那么怎么办呢，看cnt。

分两种情况，p和q的定义看代码

1、p->cnt + 1 = q->cnt

2、p->cnt + 1 != q->cnt

第一种情况，p->cnt + 1 = q->cnt说明p和q中间不包含任何其他字符，所以直接把q当作np接受新的后缀即可。

第二种情况可以通过虚拟一个节点，使得变成第一种情况

struct Node {
    int cnt; // cnt表示后缀自动机中从root走到它最多需要多少步
    int id; //表示它是第几个后缀自动机节点，指向了它，但是不知道是第几个，用id判断
    int pos; //pos表示它在原串中的位置。
    struct Node *pNext[N], *fa;
}suffixAutomaton[maxn * ], *root, *last; //大小需要开2倍，因为有一些虚拟节点
int t;  //用到第几个节点
struct Node *create(int cnt = -, struct Node *node = NULL) { //新的节点
    if (cnt != -) {
        suffixAutomaton[t].cnt = cnt, suffixAutomaton[t].fa = NULL;
        suffixAutomaton[t].id = t;  //必须要有的，不然id错误
        for (int i = ; i < N; ++i) suffixAutomaton[t].pNext[i] = NULL;
    } else {
        suffixAutomaton[t] = *node; //保留了node节点所有的指向信息
        suffixAutomaton[t].id = t; //必须要有的，不然id错误
        //可能需要注意下pos，在原串中的位置。现在pos等于原来node的pos
    }
    return &suffixAutomaton[t++];
}
void addChar(int x, int pos) { //pos表示在原串的位置
    struct Node *p = last, *np = create(p->cnt + , NULL);
    np->pos = pos, last = np; //last是最尾那个可接收后缀字符的点。
    for (; p != NULL && p->pNext[x] == NULL; p = p->fa) p->pNext[x] = np;
    if (p == NULL) {
        np->fa = root;
        return;
    }
    struct Node *q = p->pNext[x];
    if (q->cnt == p->cnt + ) { //中间没有任何字符
        np->fa = q;
        return;
    }
// p： 当前往上爬到的可以接受后缀的节点
// np：当前插入字符x的新节点
// q： q = p->pNext[x]，q就是p中指向的x字符的节点
// nq：因为q->cnt != p->cnt + 1而新建出来的模拟q的节点
    struct Node *nq = create(-, q); // 新的q节点，用来代替q，帮助np接收后缀字符
    nq->cnt = p->cnt + ; //就是需要这样，这样中间不包含任何字符
    q->fa = nq, np->fa = nq; //现在nq是包含了本来q的所有指向信息
    for (; p && p->pNext[x] == q; p = p->fa) {
        p->pNext[x] = nq;
    }
}
void init() {
    t = ;
    root = last = create(, NULL);
}
void build(char str[], int lenstr) {
    init();
    for (int i = ; i <= lenstr; ++i) addChar(str[i] - 'a', i);
}

例子"sazaa"

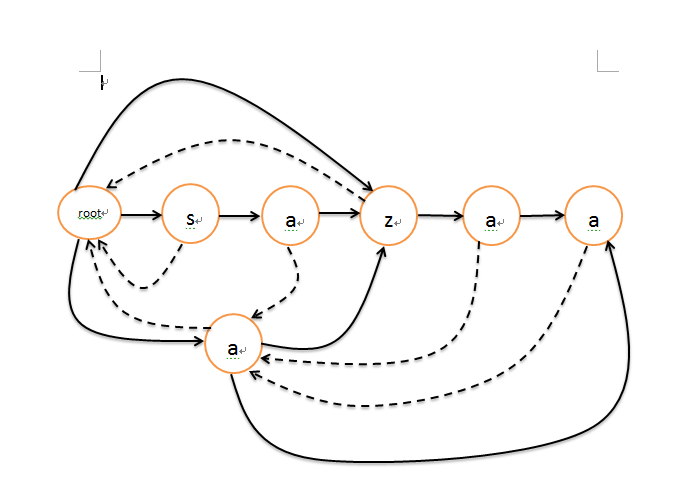
ask && question

①、识别了一个子串后，若想得到它在原串中的开始位置，假设子串长度是lensub，识别到最后一个字符在原串中是第pos个位置，那么开始位置 beginPos = = pos – lensub + 1

②、后缀自动机也能识别所有的子串，按序dfs后，当前拾得的所以字符串都是主串的一个子串，不重不漏。

例如上面的"sazaa"，dfs后

有：

s

sa

saz

saza

sazaa

a

az

aza

azaa

aa

z

za

zaa

不重不漏。

③、你说sam仅能识别后缀，那么现在为什么又能识别任何一个子串？

是这样的，sam为了不浪费空间，一个节点可能有多重身份，比如sazaa里面，最后面那个a(5)，是被虚拟出来的那个节点（最下面那个a代替的），使得最下面那个a有三个身份，一是代替a(5)和a(4)接受后缀字符，三是自己作为一个后缀'a'，其实可以在trie中很简单地用一个DFN标志当前这个节点是否能成为现在sam的后缀节点。是成为现在sam的后缀节点，因为sam的建立是在线的，是sam1的后缀节点，不一定是sam2的后缀节点。

④、一个很好的SAM教程。

http://hihocoder.com/problemset/problem/1441

#1441 : 后缀自动机一·基本概念

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

小Hi：今天我们来学习一个强大的字符串处理工具：后缀自动机（Suffix Automaton，简称SAM）。对于一个字符串S，它对应的后缀自动机是一个最小的确定有限状态自动机（DFA），接受且只接受S的后缀。

小Hi：比如对于字符串S="aabbabd"，它的后缀自动机是：

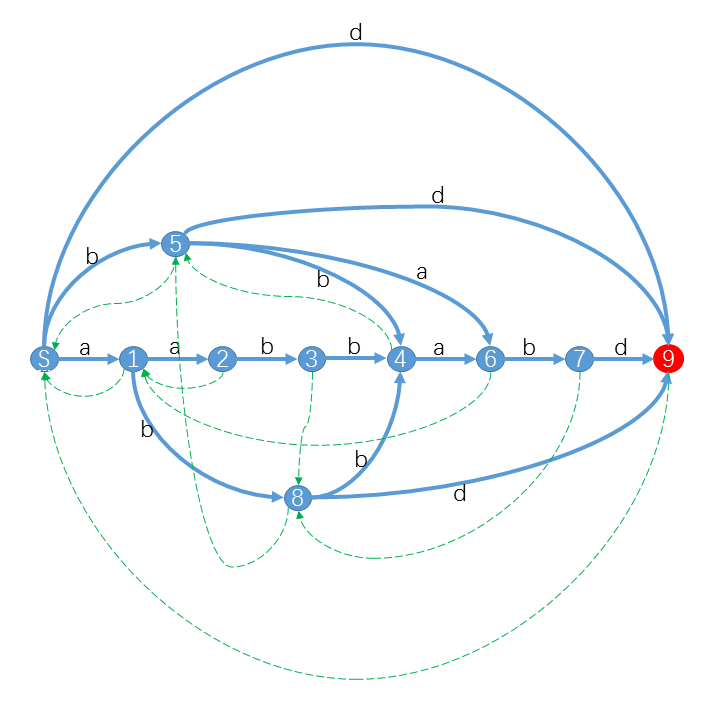
其中红色状态是终结状态。你可以发现对于S的后缀，我们都可以从S出发沿着字符标示的路径（蓝色实线）转移，最终到达终结状态。例如"bd"对应的路径是S59，"abd"对应的路径是S189，"abbabd"对应的路径是S184679。而对于不是S后缀的字符串，你会发现从S出发，最后会到达非终结状态或者“无路可走”。特别的，对于S的子串，最终会到达一个合法状态。例如"abba"路径是S1846，"bbab"路径是S5467。而对于其他不是S子串的字符串，最终会“无路可走”。 例如"aba"对应S18X，"aaba"对应S123X。（X表示没有转移匹配该字符）

小Ho：好像很厉害的样子！对于任意字符串都能构造出一个SAM吗？另外图中那些绿色虚线是什么？

小Hi：是的，任意字符串都能构造出一个SAM。我们知道SAM本质上是一个DFA，DFA可以用一个五元组 <字符集，状态集，转移函数、起始状态、终结状态集>来表示。下面我们将依次介绍对于一个给定的字符串S如何确定它对应的 状态集 和 转移函数 。至于那些绿色虚线虽然不是DFA的一部分，却是SAM的重要部分，有了这些链接SAM是如虎添翼，我们后面再细讲。

SAM的States

小Hi：这一节我们将介绍给定一个字符串S，如何确定S对应的SAM有哪些状态。首先我们先介绍一个概念 子串的结束位置集合 endpos。对于S的一个子串s，endpos(s) = s在S中所有出现的结束位置集合。还是以S="aabbabd"为例，endpos("ab") = {3, 6}，因为"ab"一共出现了2次，结束位置分别是3和6。同理endpos("a") = {1, 2, 5}, endpos("abba") = {5}。

小Hi：我们把S的所有子串的endpos都求出来。如果两个子串的endpos相等，就把这两个子串归为一类。最终这些endpos的等价类就构成的SAM的状态集合。例如对于S="aabbabd"：

状态	子串	endpos
S	空串	{0,1,2,3,4,5,6}
1	a	{1,2,5}
2	aa	{2}
3	aab	{3}
4	aabb,abb,bb	{4}
5	b	{3,4,6}
6	aabba,abba,bba,ba	{5}
7	aabbab,abbab,bbab,bab	{6}
8	ab	{3,6}
9	aabbabd,abbabd,bbabd,babd,abd,bd,d	{7}

小Ho：这些状态恰好就是上面SAM图中的状态。

小Hi：没错。此外，这些状态还有一些美妙的性质，且等我一一道来。首先对于S的两个子串s1和s2，不妨设length(s1) <= length(s2)，那么 s1是s2的后缀当且仅当endpos(s1) ⊇ endpos(s2)，s1不是s2的后缀当且仅当endpos(s1) ∩ endpos(s2) = ∅。

小Ho：我验证一下啊... 比如"ab"是"aabbab"的后缀，而endpos("ab")={3,6}，endpos("aabbab")={6}，是成立的。"b"是"ab"的后缀，endpos("b")={3,4,6}, endpos("ab")={3,6}也是成立的。"ab"不是"abb"的后缀，endpos("ab")={3,6}，endpos("abb")={4}，两者没有交集也是成立的。怎么证明呢？

小Hi：证明还是比较直观的。首先证明s1是s2的后缀=>endpos(s1) ⊇ endpos(s2)：既然s1是s2后缀，所以每次s2出现时s1以必然伴随出现，所以有endpos(s1) ⊇ endpos(s2)。再证明endpos(s1) ⊇ endpos(s2)=>s1是s2的后缀：我们知道对于S的子串s2，endpos(s2)不会是空集，所以endpos(s1) ⊇ endpos(s2)=>存在结束位置x使得s1结束于x，并且s2也结束于x，又length(s1) <= length(s2)，所以s1是s2的后缀。综上我们可知s1是s2的后缀当且仅当endpos(s1) ⊇ endpos(s2)。s1不是s2的后缀当且仅当endpos(s1) ∩ endpos(s2) = ∅是一个简单的推论，不再赘述。

小Ho：我好像对SAM的状态有一些认识了！我刚才看上面的表格就觉得SAM的一个状态里包含的子串好像有规律。考虑到SAM中的一个状态包含的子串都具有相同的endpos，那它们应该都互为后缀？

小Hi：你观察力还挺敏锐的。下面我们就来讲讲一个状态包含的子串究竟有什么关系。上文提到我们把S的所有子串按endpos分类，每一类就代表一个状态，所以我们可以认为一个状态包含了若干个子串。我们用substrings(st)表示状态st中包含的所有子串的集合，longest(st)表示st包含的最长的子串，shortest(st)表示st包含的最短的子串。例如对于状态7，substring(7)={aabbab,abbab,bbab,bab}，longest(7)=aabbab，shortest(7)=bab。

小Hi：对于一个状态st，以及任意s∈substrings(st)，都有s是longest(st)的后缀。证明比较容易，因为endpos(s)=endpos(longest(st))，所以endpos(s) ⊇ endpos(longest(st))，根据我们刚才证明的结论有s是longest(st)的后缀。

小Hi：此外，对于一个状态st，以及任意的longest(st)的后缀s，如果s的长度满足：length(shortest(st)) <= length(s) <= length(longsest(st))，那么s∈substrings(st)。 证明也是比较容易，因为：length(shortest(st)) <= length(s) <= length(longsest(st))，所以endpos(shortest(st)) ⊇ endpos(s) ⊇ endpos(longest(st))， 又endpos(shortest(st)) = endpos(longest(st))，所以endpos(shortest(st)) = endpos(s) = endpos(longest(st))，所以s∈substrings(st)。

小Ho：这么说来，substrings(st)包含的是longest(st)的一系列连续后缀？

小Hi：没错。比如你看状态7中包含的就是aabbab的长度分别是6，5，4，3的后缀；状态6包含的是aabba的长度分别是5，4，3，2的后缀。

SAM的Suffix Links

小Hi：前面我们讲到substrings(st)包含的是longest(st)的一系列连续后缀。这连续的后缀在某个地方会“断掉”。比如状态7，包含的子串依次是aabbab,abbab,bbab,bab。按照连续的规律下一个子串应该是"ab"，但是"ab"没在状态7里，你能想到这是为什么么？

小Ho：aabbab,abbab,bbab,bab的endpos都是{6}，下一个"ab"当然也在结束位置6出现过，但是"ab"还在结束位置3出现过，所以"ab"比aabbab,abbab,bbab,bab出现次数更多，于是就被分配到一个新的状态中了。

小Hi：没错，当longest(st)的某个后缀s在新的位置出现时，就会“断掉”，s会属于新的状态。比如上例中"ab"就属于状态8，endpos("ab"}={3,6}。当我们进一步考虑"ab"的下一个后缀"b"时，也会遇到相同的情况："b"还在新的位置4出现过，所以endpos("b")={3,4,6}，b属于状态5。在接下去处理"b"的后缀我们会遇到空串，endpos("")={0,1,2,3,4,5,6}，状态是起始状态S。

小Hi：于是我们可以发现一条状态序列：7->8->5->S。这个序列的意义是longest(7)即aabbab的后缀依次在状态7、8、5、S中。我们用Suffix Link这一串状态链接起来，这条link就是上图中的绿色虚线。

小Ho：原来如此。

小Hi：Suffix Links后面会有妙用，我们暂且按下不表。

SAM的Transition Function

小Hi：最后我们来介绍SAM的转移函数。对于一个状态st，我们首先找到从它开始下一个遇到的字符可能是哪些。我们将st遇到的下一个字符集合记作next(st)，有next(st) = {S[i+1] | i ∈ endpos(st)}。例如next(S)={S[1], S[2], S[3], S[4], S[5], S[6], S[7]}={a, b, d}，next(8)={S[4], S[7]}={b, d}。

小Hi：对于一个状态st来说和一个next(st)中的字符c，你会发现substrings(st)中的所有子串后面接上一个字符c之后，新的子串仍然都属于同一个状态。比如对于状态4，next(4)={a}，aabb,abb,bb后面接上字符a得到aabba，abba，bba，这些子串都属于状态6。

小Hi：所以我们对于一个状态st和一个字符c∈next(st)，可以定义转移函数trans(st, c) = x | longest(st) + c ∈ substrings(x) 。换句话说，我们在longest(st)（随便哪个子串都会得到相同的结果）后面接上一个字符c得到一个新的子串s，找到包含s的状态x，那么trans(st, c)就等于x。

小Ho：吼~ 终于把SAM中各个部分搞明白了。

小Hi：SAM的构造有时空复杂度均为O(length(S))的算法，我们将在后面介绍。这一期你可以先用暴力算法依照定义构造SAM，先对SAM有个直观认识再说。

小Ho：没问题，暴力算法我最拿手了。我先写程序去了。

习题：

字符串的最小表示法

https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=660

因为sam能识别所有的子串，那么把整个串复制一遍去后面，那么所有情况将会都考虑到。

贪心从root出发，找放在第一个地方的字母，有'a'就选'a'，没'a'就选b等等等等。

选够lenstr个，就会知道那个最小表示法的那个串是什么。然后去原串找那个位置出现了这个串即可。

我用了hash来找。给个数据：sazaa

#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
using namespace std;
#define inf (0x3f3f3f3f)
typedef long long int LL;
const int maxn = 4e5 + ;
const int N = ;
struct Node {
    int cnt, id, pos; // cnt表示在后缀自动机中从root走到它最多需要多少步
    //id表示它是第几个后缀自动机节点，指向了它，但是不知道是第几个，需要id判断
    //pos表示它在原串中的位置。
    struct Node *pNext[N], *fa;
}suffixAutomaon[maxn * ], *root, *last; //大小需要开2倍，因为有一些虚拟节点
int t; // 用到第几个节点
struct Node *create(int cnt = -, struct Node *node = NULL) { //新的节点
    if (cnt != -) {
        suffixAutomaon[t].cnt = cnt, suffixAutomaon[t].fa = NULL;
        suffixAutomaon[t].id = t;
        for (int i = ; i < N; ++i) suffixAutomaon[t].pNext[i] = NULL;
    } else {
        suffixAutomaon[t] = *node; //保留了node节点指向的信息
        suffixAutomaon[t].id = t; //必须要有的，不然id错误
    }
    return &suffixAutomaon[t++];
}
void init() {
    t = ;
    root = last = create(, NULL);
}
void addChar(int x, int pos) { //pos表示在原串的位置
    struct Node *p = last, *np = create(p->cnt + , NULL);
    np->pos = pos, last = np; //最后一个可接收后缀字符的点。
    for (; p != NULL && p->pNext[x] == NULL; p = p->fa) p->pNext[x] = np;
    if (p == NULL) {
        np->fa = root;
        return;
    }
    struct Node *q = p->pNext[x];
    if (q->cnt == p->cnt + ) { //中间没有任何字符
        np->fa = q;
        return;
    }
    struct Node *nq = create(-, q); // 新的q节点，用来代替q，帮助np接收后缀字符
    nq->cnt = p->cnt + ; //就是需要这样，这样中间不包含任何字符
    q->fa = nq, np->fa = nq; //现在nq是包含了本来q的所有指向信息
    for (; p && p->pNext[x] == q; p = p->fa) {
        p->pNext[x] = nq;
    }
}
void build(char str[], int lenstr) {
    init();
    for (int i = ; i <= lenstr; ++i) addChar(str[i] - 'a', i);
}
char str[maxn];
void dfs(int id, string s) {
    cout << s << endl;
    for (int i = ; i < N; ++i) {
        if (suffixAutomaon[id].pNext[i]) {
            char fuck = i + 'a';
            dfs(suffixAutomaon[id].pNext[i]->id, s + fuck);
        }
    }
}
int lenstr;
vector<int> pos;
bool tofind(int id) {
    if (pos.size() == lenstr) return true;
    for (int i = ; i < N; ++i) {
        if (suffixAutomaon[id].pNext[i] == NULL) continue;
        pos.push_back(suffixAutomaon[id].pNext[i]->pos);
        if (tofind(suffixAutomaon[id].pNext[i]->id)) return true;
        pos.pop_back();
    }
    return false;
}
LL f[maxn];
LL poseed[maxn];
void work() {
    scanf("%s", str + );
    lenstr = strlen(str + );
    strncpy(str + lenstr + ,  str + , lenstr);
    str[ * lenstr + ] = '\0';
//    printf("%s\n", str + 1);
    for (int i = ; i <=  * lenstr; ++i) {
        f[i] = f[i - ] *  + str[i];
    }
    build(str,  * lenstr);
    pos.clear();
    tofind();
    LL now = ;
    for (int i = ; i < pos.size(); ++i) {
//        printf("%c", str[pos[i]]);
        now = now *  + str[pos[i]];
    }
//    printf("\n");
//    printf("%d\n", pos[0]);
    for (int i = lenstr; i <=  * lenstr; ++i) {
        LL t = f[i] - poseed[lenstr] * f[i - lenstr];
        if (t == now) {
            printf("%d\n", i - lenstr + );
            return;
        }
    }
    assert(false);
}
int main() {
#ifdef local
    freopen("data.txt", "r", stdin);
//    freopen("data.txt", "w", stdout);
#endif
    poseed[] = ;
    for (int i = ; i <= maxn - ; ++i) poseed[i] = poseed[i - ] * ;
    int t;
    scanf("%d", &t);
    while (t--) work();
    return ;
}

上面这题其实不用hash

怎么找pos？

选够了lenstr个后，肯定知道最后一个在原串中是什么位置，然后那个位置 - lenstr +１就是答案。

（因为字符串长度是ｌｅｎｓｔｒ嘛）

#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
using namespace std;
#define inf (0x3f3f3f3f)
typedef long long int LL;
const int maxn = 4e5 + ;
const int N = ;
struct Node {
    int cnt, id, pos; // cnt表示在后缀自动机中从root走到它最多需要多少步
    //id表示它是第几个后缀自动机节点，指向了它，但是不知道是第几个，需要id判断
    //pos表示它在原串中的位置。
    struct Node *pNext[N], *fa;
}suffixAutomaon[maxn * ], *root, *last; //大小需要开2倍，因为有一些虚拟节点
int t; // 用到第几个节点
struct Node *create(int cnt = -, struct Node *node = NULL) { //新的节点
    if (cnt != -) {
        suffixAutomaon[t].cnt = cnt, suffixAutomaon[t].fa = NULL;
        suffixAutomaon[t].id = t;
        for (int i = ; i < N; ++i) suffixAutomaon[t].pNext[i] = NULL;
    } else {
        suffixAutomaon[t] = *node; //保留了node节点指向的信息
        suffixAutomaon[t].id = t; //必须要有的，不然id错误
    }
    return &suffixAutomaon[t++];
}
void init() {
    t = ;
    root = last = create(, NULL);
}
void addChar(int x, int pos) { //pos表示在原串的位置
    struct Node *p = last, *np = create(p->cnt + , NULL);
    np->pos = pos, last = np; //最后一个可接收后缀字符的点。
    for (; p != NULL && p->pNext[x] == NULL; p = p->fa) p->pNext[x] = np;
    if (p == NULL) {
        np->fa = root;
        return;
    }
    struct Node *q = p->pNext[x];
    if (q->cnt == p->cnt + ) { //中间没有任何字符
        np->fa = q;
        return;
    }
    struct Node *nq = create(-, q); // 新的q节点，用来代替q，帮助np接收后缀字符
    nq->cnt = p->cnt + ; //就是需要这样，这样中间不包含任何字符
    q->fa = nq, np->fa = nq; //现在nq是包含了本来q的所有指向信息
    for (; p && p->pNext[x] == q; p = p->fa) {
        p->pNext[x] = nq;
    }
}
void build(char str[], int lenstr) {
    init();
    for (int i = ; i <= lenstr; ++i) addChar(str[i] - 'a', i);
}
char str[maxn];
void dfs(int id, string s) {
    cout << s << endl;
    for (int i = ; i < N; ++i) {
        if (suffixAutomaon[id].pNext[i]) {
            char fuck = i + 'a';
            dfs(suffixAutomaon[id].pNext[i]->id, s + fuck);
        }
    }
}
int lenstr;
vector<int> pos;
bool tofind(int id) {
    if (pos.size() == lenstr) return true;
    for (int i = ; i < N; ++i) {
        if (suffixAutomaon[id].pNext[i] == NULL) continue;
        pos.push_back(suffixAutomaon[id].pNext[i]->pos);
        if (tofind(suffixAutomaon[id].pNext[i]->id)) return true;
        pos.pop_back();
    }
    return false;
}
LL f[maxn];
LL poseed[maxn];
void work() {
    scanf("%s", str + );
    lenstr = strlen(str + );
    strncpy(str + lenstr + ,  str + , lenstr);
    str[ * lenstr + ] = '\0';
//    printf("%s\n", str + 1);
    for (int i = ; i <=  * lenstr; ++i) {
        f[i] = f[i - ] *  + str[i];
    }
    build(str,  * lenstr);
    pos.clear();
    tofind();
    cout << (pos.back() - lenstr + ) << endl;
//    LL now = 0;
//    for (int i = 0; i < pos.size(); ++i) {
////        printf("%c", str[pos[i]]);
//        now = now * 131 + str[pos[i]];
//    }
////    printf("\n");
////    printf("%d\n", pos[0]);
//    for (int i = lenstr; i <= 2 * lenstr; ++i) {
//        LL t = f[i] - poseed[lenstr] * f[i - lenstr];
//        if (t == now) {
//            printf("%d\n", i - lenstr + 1);
//            return;
//        }
//    }
//    assert(false);
}
int main() {
#ifdef local
    freopen("data.txt", "r", stdin);
//    freopen("data.txt", "w", stdout);
#endif
    poseed[] = ;
    for (int i = ; i <= maxn - ; ++i) poseed[i] = poseed[i - ] * ;
    int t;
    scanf("%d", &t);
    while (t--) work();
    return ;
}

两个串的最长公共子串。

Longest Common Substring SPOJ - LCS

http://www.spoj.com/problems/LCS/en/

其实是后缀数组裸体，直接后缀数组然后枚举每一个height合法的情况的min(sa[i - 1], sa[i]) <= lenstr && max(sa[i - 1], sa[i]) >= lenstr + 1

然后更新答案即可。（后缀数组那个mx应该是128而不是lenstr，用到了更大的再用更大的）

复杂度(nlogn)

#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
using namespace std;
#define inf (0x3f3f3f3f)
typedef long long int LL;
const int maxn =  *  + ;
int sa[maxn], x[maxn], y[maxn], book[maxn]; //book[]大小起码是lenstr，book[rank[]]
bool cmp(int r[], int a, int b, int len) { //这个必须是int r[]，
    return r[a] == r[b] && r[a + len] == r[b + len];
}
void da(char str[], int sa[], int lenstr, int mx) {
    int *fir = x, *sec = y, *ToChange;
    for (int i = ; i <= mx; ++i) book[i] = ; //清0
    for (int i = ; i <= lenstr; ++i) {
        fir[i] = str[i];  //开始的rank数组，只保留相对大小即可，开始就是str[]
        book[str[i]]++; //统计不同字母的个数
    }
    for (int i = ; i <= mx; ++i) book[i] += book[i - ]; //统计 <= 这个字母的有多少个元素
    for (int i = lenstr; i >= ; --i) sa[book[fir[i]]--] = i;
// <=str[i]这个字母的有x个，那么，排第x的就应该是这个i的位置了。
    //倒过来排序，是为了确保相同字符的时候，前面的就先在前面出现。
    //p是第二个关键字0的个数
    for (int j = , p = ; p <= lenstr; j <<= , mx = p) {  //字符串长度为j的比较
        //现在求第二个关键字，然后合并（合并的时候按第一关键字优先合并）
        p = ;
        for (int i = lenstr - j + ; i <= lenstr; ++i) sec[++p] = i;
//这些位置，再跳j格就是越界了的，所以第二关键字是0，排在前面
        for (int i = ; i <= lenstr; ++i)
            if (sa[i] > j)  //如果排名第i的起始位置在长度j之后
                sec[++p] = sa[i] - j;
//减去这个长度j，表明第sa[i] - j这个位置的第二个是从sa[i]处拿的，排名靠前也//正常，因为sa[i]排名是递增的
        //sec[]保存的是下标，现在对第一个关键字排序
        for (int i = ; i <= mx; ++i) book[i] = ; //清0
        for (int i = ; i <= lenstr; ++i) book[fir[sec[i]]]++;
        for (int i = ; i <= mx; ++i) book[i] += book[i - ];
        for (int i = lenstr; i >= ; --i) sa[book[fir[sec[i]]]--] = sec[i];
//因为sec[i]才是对应str[]的下标
//现在要把第二关键字的结果，合并到第一关键字那里。同时我需要用到第一关键//字保存的记录，所以用指针交换的方式达到快速交换数组中的值
        ToChange = fir, fir = sec, sec = ToChange;
        fir[sa[]] = ; //固定的是0 因为sa[1]固定是lenstr那个0
        p = ;
        for (int i = ; i <= lenstr; ++i)  //fir是当前的rank值，sec是前一次的rank值
            fir[sa[i]] = cmp(sec, sa[i - ], sa[i], j) ? p -  : p++;
    }
    return ;
}
int height[maxn], RANK[maxn];
void calcHight(char str[], int sa[], int lenstr) {
    for (int i = ; i <= lenstr; ++i) RANK[sa[i]] = i; //O(n)处理出rank[]
    int k = ;
    for (int i = ; i <= lenstr - ; ++i) {
//最后一位不用算，最后一位排名一定是1，然后sa[0]就尴尬了
        k -= k > ;
        int j = sa[RANK[i] - ]; //排名在i前一位的那个串，相似度最高
        while (str[j + k] == str[i + k]) ++k;
        height[RANK[i]] = k;
    }
    return ;
}
char str[maxn], sub[maxn];
void work() {
    scanf("%s%s", str + , sub + );
    int lenstr = strlen(str + ), lensub = strlen(sub + );
    str[lenstr + ] = '';
    strcpy(str + lenstr + , sub + );
    str[lenstr + lensub + ] = '';
    str[lenstr + lensub + ] = '\0';
    int tot = lenstr + lensub + ;
    da(str, sa, tot + , );
    calcHight(str, sa, tot + );
    int ans = ;
//    printf("%s\n", str + 1);
    for (int i = ; i <= tot + ; ++i) {
//        printf("%d ", height[i]);
//        printf("%d ", sa[i]);
        int mi = min(sa[i - ], sa[i]);
        int mx = max(sa[i - ], sa[i]);
        if (mi <= lenstr && mx >= lenstr + ) {
            ans = max(ans, height[i]);
        }
    }
    printf("%d\n", ans);
}
int main() {
#ifdef local
    freopen("data.txt", "r", stdin);
//    freopen("data.txt", "w", stdout);
#endif
    work();
    return ;
}

用sam的话，首先建立第一个串的sam，然后用第二个串在sam中爬，怎么爬？

因为知道sam是能识别所有子串的。那么直接从第二个串开头位置开始枚举，从sam的root出发。

如果当前走到的sam节点能识别现在枚举的字符x，那么走过去，同时匹配数量++

如果不能，则需要走p->fa使得去到某一个能识别x字符的节点，

那么这个时候匹配了多少个？

ans = 走到这个sam节点所需的最大步数 +１个，

＋１是因为匹配了ｘ字符，

注意到ｓａｍ中每个节点的fa要么是和它相同的字符，要么就是root

而且它的p->fa->cnt肯定不会比p->cnt大，意思就是本来匹配过的字符，现在同样能匹配。

复杂度O(n)

#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
using namespace std;
#define inf (0x3f3f3f3f)
typedef long long int LL;
const int maxn =  *  + ;
const int N = ;
struct Node {
    int cnt, id, pos; // cnt表示在后缀自动机中从root走到它最多需要多少步
    //id表示它是第几个后缀自动机节点，指向了它，但是不知道是第几个，需要id判断
    //pos表示它在原串中的位置。
    struct Node *pNext[N], *fa;
}suffixAutomaon[maxn * ], *root, *last; //大小需要开2倍，因为有一些虚拟节点
int t; // 用到第几个节点
struct Node *create(int cnt = -, struct Node *node = NULL) { //新的节点
    if (cnt != -) {
        suffixAutomaon[t].cnt = cnt, suffixAutomaon[t].fa = NULL;
        suffixAutomaon[t].id = t;
        for (int i = ; i < N; ++i) suffixAutomaon[t].pNext[i] = NULL;
    } else {
        suffixAutomaon[t] = *node; //保留了node节点指向的信息
        suffixAutomaon[t].id = t; //必须要有的，不然id错误
    }
    return &suffixAutomaon[t++];
}
void init() {
    t = ;
    root = last = create(, NULL);
}
void addChar(int x, int pos) { //pos表示在原串的位置
    struct Node *p = last, *np = create(p->cnt + , NULL);
    np->pos = pos, last = np; //最后一个可接收后缀字符的点。
    for (; p != NULL && p->pNext[x] == NULL; p = p->fa) p->pNext[x] = np;
    if (p == NULL) {
        np->fa = root;
        return;
    }
    struct Node *q = p->pNext[x];
    if (q->cnt == p->cnt + ) { //中间没有任何字符
        np->fa = q;
        return;
    }
    struct Node *nq = create(-, q); // 新的q节点，用来代替q，帮助np接收后缀字符
    nq->cnt = p->cnt + ; //就是需要这样，这样中间不包含任何字符
    q->fa = nq, np->fa = nq; //现在nq是包含了本来q的所有指向信息
    for (; p && p->pNext[x] == q; p = p->fa) {
        p->pNext[x] = nq;
    }
}
void build(char str[], int lenstr) {
    init();
    for (int i = ; i <= lenstr; ++i) addChar(str[i] - 'a', i);
}
char str[maxn], sub[maxn];
void work() {
    scanf("%s%s", str + , sub + );
    int lenstr = strlen(str + ), lensub = strlen(sub + );
    build(str, lenstr);
    int ans = ;
    int len = ;
    struct Node *p = root;
    for (int i = ; i <= lensub; ++i) {
        int x = sub[i] - 'a';
        if (p->pNext[x]) {
            p = p->pNext[x];
            len++;
        } else {
            while (p && !p->pNext[x]) p = p->fa;
            if (p == NULL) {
                len = ;
                p = root;
            } else {
                len = p->cnt + ;
                p = p->pNext[x];
            }
        }
        ans = max(ans, len);
    }
    cout << ans << endl;
}
int main() {
#ifdef local
    freopen("data.txt", "r", stdin);
//    freopen("data.txt", "w", stdout);
#endif
    work();
    return ;
}

还有一题是应用了SAM的在线功能

http://www.cnblogs.com/liuweimingcprogram/p/7296402.html

SAM求不同子串个数。

http://hihocoder.com/problemset/problem/1445?sid=1147665

我们知道对于SAM的每一个状态，都能识别若干个子串，

记这些子串的最大长度是longest(st)，最小长度是small(st)，那么一共出现了mx - mi + 1个子串，所以只需要build的时候

找到mxcnt和micnt即可。注意每个状态能识别的子串都是不一样的。

#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
using namespace std;
#define inf (0x3f3f3f3f)
typedef long long int LL;
const int maxn =  + , N = ;
struct Node {
    int mxCnt; //mxCnt表示后缀自动机中当前节点识别子串的最大长度
    int miCnt; //miCnt表示后缀自动机中当前节点识别子串的最小长度
    int id; //表示它是第几个后缀自动机节点，指向了它，但是不知道是第几个，用id判断
    int pos; //pos表示它在原串中的位置。
    struct Node *pNext[N], *fa;
}suffixAutomaton[maxn * ], *root, *last; //大小需要开2倍，因为有一些虚拟节点
int t;  //用到第几个节点
struct Node *create(int mxCnt = -, struct Node *node = NULL) { //新的节点
    if (mxCnt != -) {
        suffixAutomaton[t].mxCnt = mxCnt, suffixAutomaton[t].fa = NULL;
        suffixAutomaton[t].id = t;  //必须要有的，不然id错误
        for (int i = ; i < N; ++i) suffixAutomaton[t].pNext[i] = NULL;
    } else {
        suffixAutomaton[t] = *node; //保留了node节点所有的指向信息
        suffixAutomaton[t].id = t; //必须要有的，不然id错误
        //可能需要注意下pos，在原串中的位置。现在pos等于原来node的pos
    }
    return &suffixAutomaton[t++];
}
void addChar(int x, int pos) { //pos表示在原串的位置
    struct Node *p = last, *np = create(p->mxCnt + , NULL);
    np->pos = pos, last = np; //last是最尾那个可接收后缀字符的点。
    for (; p != NULL && p->pNext[x] == NULL; p = p->fa) p->pNext[x] = np;
    if (p == NULL) {
        np->fa = root;
        np->miCnt = ; // 从根节点引一条边过来
        return;
    }
    struct Node *q = p->pNext[x];
    if (q->mxCnt == p->mxCnt + ) { //中间没有任何字符
        np->fa = q;
        np->miCnt = q->mxCnt + ; // 7-->8的那些"ab"，自己是"bab"长度是2+1
        return;
    }
    // p： 当前往上爬到的可以接受后缀的节点
    // np：当前插入字符x的新节点
    // q： q = p->pNext[x]，q就是p中指向的x字符的节点
    // nq：因为q->cnt != p->cnt + 1而新建出来的模拟q的节点
    struct Node *nq = create(-, q); // 新的q节点，用来代替q，帮助np接收后缀字符
    nq->mxCnt = p->mxCnt + ; //就是需要这样，这样中间不包含任何字符
    q->miCnt = nq->mxCnt + , np->miCnt = nq->mxCnt + ;
    q->fa = nq, np->fa = nq; //现在nq是包含了本来q的所有指向信息
    for (; p && p->pNext[x] == q; p = p->fa) {
        p->pNext[x] = nq;
    }
}
void init() {
    t = ;
    root = last = create(, NULL);
}
void build(char str[], int lenstr) {
    init();
    for (int i = ; i <= lenstr; ++i) addChar(str[i] - 'a', i);
}
char str[maxn];
int lenstr;
void work() {
    scanf("%s", str + );
    lenstr = strlen(str + );
    build(str, lenstr);
    LL ans = ;
    for (int i = ; i <= t - ; ++i) {
        ans += suffixAutomaton[i].mxCnt - suffixAutomaton[i].miCnt + ;
    }
    cout << ans << endl;
}
int main() {
#ifdef local
    freopen("data.txt", "r", stdin);
//    freopen("data.txt", "w", stdout);
#endif
    work();
    return ;
}

Substrings SPOJ - NSUBSTR

这题就

http://www.spoj.com/problems/NSUBSTR/en/

http://hihocoder.com/problemset/problem/1449?sid=1149820

上面有详解

主要思路，如果知道每一个节点的endpos大小，那么是很好做的。

endpos意思就是当前这个节点所能识别的子串，在原串中的结束位置是什么。

如果"ab"在原串中结束位置是3， 6，那么子串"ab"出现次数就是2次。（这里隐含着长度是1的至少出现了2次）

而每个节点所能识别的子串长度是从    miCnt --- mxCnt的，所以ans[miCnt --- mxCnt] = max(endpos)

关键是怎么求endpos。

通过拓扑 + suffixLink求。

主要就是如果fa由x和y组成，那么|fa|   >=  |x|  + |y|

#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
using namespace std;
#define inf (0x3f3f3f3f)
typedef long long int LL;
const int maxn =  + , N = ;
struct Node {
    int mxCnt; //mxCnt表示后缀自动机中当前节点识别子串的最大长度
    int miCnt; //miCnt表示后缀自动机中当前节点识别子串的最小长度
    int id; //表示它是第几个后缀自动机节点，指向了它，但是不知道是第几个，用id判断
    int pos; //pos表示它在原串中的位置。
    bool flag; //表示当前节点是否能识别前缀
    struct Node *pNext[N], *fa;
}suffixAutomaton[maxn * ], *root, *last; //大小需要开2倍，因为有一些虚拟节点
int t;  //用到第几个节点
struct Node *create(int mxCnt = -, struct Node *node = NULL) { //新的节点
    if (mxCnt != -) {
        suffixAutomaton[t].mxCnt = mxCnt, suffixAutomaton[t].fa = NULL;
        for (int i = ; i < N; ++i) suffixAutomaton[t].pNext[i] = NULL;
    } else {
        suffixAutomaton[t] = *node; //保留了node节点所有的指向信息
        //可能需要注意下pos，在原串中的位置。现在pos等于原来node的pos
    }
    suffixAutomaton[t].id = t;  //必须要有的，不然id错误
    suffixAutomaton[t].flag = false;
    return &suffixAutomaton[t++];
}
void addChar(int x, int pos) { //pos表示在原串的位置
    struct Node *p = last, *np = create(p->mxCnt + , NULL);
    np->flag = true;
    np->pos = pos, last = np; //last是最尾那个可接收后缀字符的点。
    for (; p != NULL && p->pNext[x] == NULL; p = p->fa) p->pNext[x] = np;
    if (p == NULL) {
        np->fa = root;
        np->miCnt = ; // 从根节点引一条边过来
        return;
    }
    struct Node *q = p->pNext[x];
    if (q->mxCnt == p->mxCnt + ) { //中间没有任何字符
        np->fa = q;
        np->miCnt = q->mxCnt + ; // q是7-->8的那些"ab"，np是"bab"长度是2+1
        return;
    }
    // p： 当前往上爬到的可以接受后缀的节点
    // np：当前插入字符x的新节点
    // q： q = p->pNext[x]，q就是p中指向的x字符的节点
    // nq：因为q->cnt != p->cnt + 1而新建出来的模拟q的节点
    struct Node *nq = create(-, q); // 新的q节点，用来代替q，帮助np接收后缀字符
    nq->mxCnt = p->mxCnt + ; //就是需要这样，这样中间不包含任何字符
    q->miCnt = nq->mxCnt + , np->miCnt = nq->mxCnt + ;
    q->fa = nq, np->fa = nq; //现在nq是包含了本来q的所有指向信息
    for (; p && p->pNext[x] == q; p = p->fa) {
        p->pNext[x] = nq;
    }
}
void init() {
    t = ;
    root = last = create(, NULL);
}
void build(char str[], int lenstr) {
    init();
    for (int i = ; i <= lenstr; ++i) addChar(str[i] - 'a', i);
}
char str[maxn * ];
int lenstr;
int in[maxn * ];
int dp[maxn * ];
queue<int> que;
int ans[maxn * ];
void work() {
    scanf("%s", str + );
    lenstr = strlen(str + );
    build(str, lenstr);
    for (int i = ; i < t; ++i) {
        in[suffixAutomaton[i].fa->id]++;
        if (suffixAutomaton[i].flag) dp[i] = ;
    }
    for (int i = ; i < t; ++i) {
        if (in[i] == ) que.push(i);
    }
    while (!que.empty()) {
        int cur = que.front();
        que.pop();
        if (!cur) break;
        dp[suffixAutomaton[cur].fa->id] += dp[cur];
        in[suffixAutomaton[cur].fa->id]--;
        if (in[suffixAutomaton[cur].fa->id] == ) que.push(suffixAutomaton[cur].fa->id);
    }
    for (int i = ; i < t; ++i) {
        ans[suffixAutomaton[i].mxCnt] = max(ans[suffixAutomaton[i].mxCnt], dp[suffixAutomaton[i].id]);
    }
    for (int i = lenstr - ; i >= ; --i) {
        ans[i] = max(ans[i], ans[i + ]);
    }
    for (int i = ; i <= lenstr; ++i) {
        printf("%d\n", ans[i]);
    }
}
int main() {
#ifdef local
    freopen("data.txt", "r", stdin);
//    freopen("data.txt", "w", stdout);
#endif
    work();
    return ;
}

2017年9月4日 00:29:36

自己给自己出了一道题

给定一个文本串str，一个模式串sub

求解sub的每一个前缀，在文本串str中的出现次数，允许重叠。

首先对str建立sam，然后用sub在sam中爬，如果不能识别了，也就不能识别后面的了。此时候ans应该是0

如果能，那么出现次数就是endpos的大小。这个使用dp预处理出来即可。

str:  　　aabaabbaab
sub:  　  aabba

ans :      6 3 3 1 1

#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
using namespace std;
#define inf (0x3f3f3f3f)
typedef long long int LL;
const int maxn =  + , N = ;
struct Node {
    int mxCnt; //mxCnt表示后缀自动机中当前节点识别子串的最大长度
    int miCnt; //miCnt表示后缀自动机中当前节点识别子串的最小长度
    int id; //表示它是第几个后缀自动机节点，指向了它，但是不知道是第几个，用id判断
    int pos; //pos表示它在原串中的位置。
    bool flag; //表示当前节点是否能识别前缀
    struct Node *pNext[N], *fa;
}suffixAutomaton[maxn * ], *root, *last; //大小需要开2倍，因为有一些虚拟节点
int t;  //用到第几个节点
struct Node *create(int mxCnt = -, struct Node *node = NULL) { //新的节点
    if (mxCnt != -) {
        suffixAutomaton[t].mxCnt = mxCnt, suffixAutomaton[t].fa = NULL;
        for (int i = ; i < N; ++i) suffixAutomaton[t].pNext[i] = NULL;
    } else {
        suffixAutomaton[t] = *node; //保留了node节点所有的指向信息
        //可能需要注意下pos，在原串中的位置。现在pos等于原来node的pos
    }
    suffixAutomaton[t].id = t;  //必须要有的，不然id错误
    suffixAutomaton[t].flag = false;
    return &suffixAutomaton[t++];
}
void addChar(int x, int pos) { //pos表示在原串的位置
    struct Node *p = last, *np = create(p->mxCnt + , NULL);
    np->flag = true;
    np->pos = pos, last = np; //last是最尾那个可接收后缀字符的点。
    for (; p != NULL && p->pNext[x] == NULL; p = p->fa) p->pNext[x] = np;
    if (p == NULL) {
        np->fa = root;
        np->miCnt = ; // 从根节点引一条边过来
        return;
    }
    struct Node *q = p->pNext[x];
    if (q->mxCnt == p->mxCnt + ) { //中间没有任何字符
        np->fa = q;
        np->miCnt = q->mxCnt + ; // q是7-->8的那些"ab"，np是"bab"长度是2+1
        return;
    }
    // p： 当前往上爬到的可以接受后缀的节点
    // np：当前插入字符x的新节点
    // q： q = p->pNext[x]，q就是p中指向的x字符的节点
    // nq：因为q->cnt != p->cnt + 1而新建出来的模拟q的节点
    struct Node *nq = create(-, q); // 新的q节点，用来代替q，帮助np接收后缀字符
    nq->mxCnt = p->mxCnt + ; //就是需要这样，这样中间不包含任何字符
    q->miCnt = nq->mxCnt + , np->miCnt = nq->mxCnt + ;
    q->fa = nq, np->fa = nq; //现在nq是包含了本来q的所有指向信息
    for (; p && p->pNext[x] == q; p = p->fa) {
        p->pNext[x] = nq;
    }
}
void init() {
    t = ;
    root = last = create(, NULL);
}
void build(char str[], int lenstr) {
    init();
    for (int i = ; i <= lenstr; ++i) addChar(str[i] - 'a', i);
}
char str[maxn * ];
int lenstr;
int in[maxn * ];
int dp[maxn * ];
queue<int> que;
int ans[maxn * ];
char sub[maxn];
void work() {
    scanf("%s", str + );
    lenstr = strlen(str + );
    build(str, lenstr);
    for (int i = ; i < t; ++i) {
        in[suffixAutomaton[i].fa->id]++;
        if (suffixAutomaton[i].flag) dp[i] = ;
    }
    for (int i = ; i < t; ++i) {
        if (in[i] == ) que.push(i);
    }
    while (!que.empty()) {
        int cur = que.front();
        que.pop();
        if (!cur) break;
        dp[suffixAutomaton[cur].fa->id] += dp[cur];
        in[suffixAutomaton[cur].fa->id]--;
        if (in[suffixAutomaton[cur].fa->id] == ) que.push(suffixAutomaton[cur].fa->id);
    }
    scanf("%s", sub + );
    int lensub = strlen(sub + );
    int now = ;
    for (int i = ; i <= lensub; ++i) {
        if (suffixAutomaton[now].pNext[sub[i] - 'a']) {
            now = suffixAutomaton[now].pNext[sub[i] - 'a']->id;
            ans[i] = dp[now];
        } else break;
    }
    for (int i = ; i <= lensub; ++i) {
        printf("%d ", ans[i]);
    }
}
int main() {
#ifdef local
    freopen("data.txt", "r", stdin);
//    freopen("data.txt", "w", stdout);
#endif
    work();
    return ;
}

这题嘛，可以

用了sam做了但是MLE了

http://acm.hdu.edu.cn/showproblem.php?pid=6153

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <queue>
#include <algorithm>
#define IOS ios::sync_with_stdio(false)
using namespace std;
#define inf (0x3f3f3f3f)
typedef long long int LL;
const int maxn = 1e6 + , N = ;
struct Node {
    int mxCnt; //mxCnt表示后缀自动机中当前节点识别子串的最大长度
    int miCnt; //miCnt表示后缀自动机中当前节点识别子串的最小长度
    int id; //表示它是第几个后缀自动机节点，指向了它，但是不知道是第几个，用id判断
    bool flag; //表示当前节点是否能识别前缀
    struct Node *pNext[N], *fa;
}suffixAutomaton[maxn], *root, *last; //大小需要开2倍，因为有一些虚拟节点
int t;  //用到第几个节点
struct Node *create(int mxCnt = -, struct Node *node = NULL) { //新的节点
    if (mxCnt != -) {
        suffixAutomaton[t].mxCnt = mxCnt, suffixAutomaton[t].fa = NULL;
        for (int i = ; i < N; ++i) suffixAutomaton[t].pNext[i] = NULL;
    } else {
        suffixAutomaton[t] = *node; //保留了node节点所有的指向信息
        //可能需要注意下pos，在原串中的位置。现在pos等于原来node的pos
    }
    suffixAutomaton[t].id = t;  //必须要有的，不然id错误
    suffixAutomaton[t].flag = false;
    return &suffixAutomaton[t++];
}
void addChar(int x, int pos) { //pos表示在原串的位置
    struct Node *p = last, *np = create(p->mxCnt + , NULL);
    np->flag = true;
    last = np; //last是最尾那个可接收后缀字符的点。
    for (; p != NULL && p->pNext[x] == NULL; p = p->fa) p->pNext[x] = np;
    if (p == NULL) {
        np->fa = root;
        np->miCnt = ; // 从根节点引一条边过来
        return;
    }
    struct Node *q = p->pNext[x];
    if (q->mxCnt == p->mxCnt + ) { //中间没有任何字符
        np->fa = q;
        np->miCnt = q->mxCnt + ; // q是7-->8的那些"ab"，np是"bab"长度是2+1
        return;
    }
    // p： 当前往上爬到的可以接受后缀的节点
    // np：当前插入字符x的新节点
    // q： q = p->pNext[x]，q就是p中指向的x字符的节点
    // nq：因为q->cnt != p->cnt + 1而新建出来的模拟q的节点
    struct Node *nq = create(-, q); // 新的q节点，用来代替q，帮助np接收后缀字符
    nq->mxCnt = p->mxCnt + ; //就是需要这样，这样中间不包含任何字符
    q->miCnt = nq->mxCnt + , np->miCnt = nq->mxCnt + ;
    q->fa = nq, np->fa = nq; //现在nq是包含了本来q的所有指向信息
    for (; p && p->pNext[x] == q; p = p->fa) {
        p->pNext[x] = nq;
    }
}
void init() {
    t = ;
    root = last = create(, NULL);
}
void build(char str[], int lenstr) {
    init();
    for (int i = ; i <= lenstr; ++i) {
        if (str[i] >= 'a' && str[i] <= 'z')
            addChar(str[i] - 'a', i);
        else addChar(str[i] - 'A' + , i);
    }
}
char str[maxn];
int lenstr;
int in[maxn];
int dp[maxn];
int que[maxn];
int ans[maxn];
char sub[maxn];
const int MOD = 1e9 + ;
void work() {
    scanf("%s", str + );
    lenstr = strlen(str + );
    reverse(str + , str +  + lenstr);
    build(str, lenstr);
    for (int i = ; i < t; ++i) {
        in[suffixAutomaton[i].fa->id]++;
        if (suffixAutomaton[i].flag) dp[i] = ;
    }
    int head = , tail = ;
    for (int i = ; i < t; ++i) {
        if (in[i] == ) que[tail++] = i;
    }
    while (head < tail) {
        int cur = que[head++];
        if (!cur) break;
        dp[suffixAutomaton[cur].fa->id] += dp[cur];
        in[suffixAutomaton[cur].fa->id]--;
        if (in[suffixAutomaton[cur].fa->id] == ) que[tail++] = suffixAutomaton[cur].fa->id;
    }
    scanf("%s", sub + );
    int lensub = strlen(sub + );
    reverse(sub + , sub +  + lensub);
    int now = ;
    int en = lensub + ;
    for (int i = ; i <= lensub; ++i) {
        int id;
        if (sub[i] >= 'a' && sub[i] <= 'z') id = sub[i] - 'a';
        else id = sub[i] - 'A' + ;
        if (suffixAutomaton[now].pNext[id]) {
            now = suffixAutomaton[now].pNext[id]->id;
            ans[i] = dp[now];
        } else {
            en = i;
            break;
        }
    }
    LL haha = ;
    for (int i = ; i < en; ++i) {
        haha += 1LL * i * ans[i];
        if (haha >= MOD) haha %= MOD;
    }
    printf("%I64d\n", haha);
}
int main() {
#ifdef local
    freopen("data.txt", "r", stdin);
//    freopen("data.txt", "w", stdout);
#endif
    int t;
    scanf("%d", &t);
    while (t--)
        work();
    return ;
}

确实可以我做了。这题

http://codeforces.com/contest/432/problem/D

#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
using namespace std;
#define inf (0x3f3f3f3f)
typedef long long int LL;
const int maxn = 1e5 + , N = ;
struct Node {
    int mxCnt; //mxCnt表示后缀自动机中当前节点识别子串的最大长度
    int miCnt; //miCnt表示后缀自动机中当前节点识别子串的最小长度
    int id; //表示它是第几个后缀自动机节点，指向了它，但是不知道是第几个，用id判断
    int pos; //pos表示它在原串中的位置。
    bool flag; //表示当前节点是否能识别前缀
    struct Node *pNext[N], *fa;
}suffixAutomaton[maxn * ], *root, *last; //大小需要开2倍，因为有一些虚拟节点
int t;  //用到第几个节点
struct Node *create(int mxCnt = -, struct Node *node = NULL) { //新的节点
    if (mxCnt != -) {
        suffixAutomaton[t].mxCnt = mxCnt, suffixAutomaton[t].fa = NULL;
        for (int i = ; i < N; ++i) suffixAutomaton[t].pNext[i] = NULL;
    } else {
        suffixAutomaton[t] = *node; //保留了node节点所有的指向信息
        //可能需要注意下pos，在原串中的位置。现在pos等于原来node的pos
    }
    suffixAutomaton[t].id = t;  //必须要有的，不然id错误
    suffixAutomaton[t].flag = false;
    return &suffixAutomaton[t++];
}
void addChar(int x, int pos) { //pos表示在原串的位置
    struct Node *p = last, *np = create(p->mxCnt + , NULL);
    np->flag = true;
    np->pos = pos, last = np; //last是最尾那个可接收后缀字符的点。
    for (; p != NULL && p->pNext[x] == NULL; p = p->fa) p->pNext[x] = np;
    if (p == NULL) {
        np->fa = root;
        np->miCnt = ; // 从根节点引一条边过来
        return;
    }
    struct Node *q = p->pNext[x];
    if (q->mxCnt == p->mxCnt + ) { //中间没有任何字符
        np->fa = q;
        np->miCnt = q->mxCnt + ; // q是7-->8的那些"ab"，np是"bab"长度是2+1
        return;
    }
    // p： 当前往上爬到的可以接受后缀的节点
    // np：当前插入字符x的新节点
    // q： q = p->pNext[x]，q就是p中指向的x字符的节点
    // nq：因为q->cnt != p->cnt + 1而新建出来的模拟q的节点
    struct Node *nq = create(-, q); // 新的q节点，用来代替q，帮助np接收后缀字符
    nq->mxCnt = p->mxCnt + ; //就是需要这样，这样中间不包含任何字符
    q->miCnt = nq->mxCnt + , np->miCnt = nq->mxCnt + ;
    q->fa = nq, np->fa = nq; //现在nq是包含了本来q的所有指向信息
    for (; p && p->pNext[x] == q; p = p->fa) {
        p->pNext[x] = nq;
    }
}
void init() {
    t = ;
    root = last = create(, NULL);
}
void build(char str[], int lenstr) {
    init();
    for (int i = ; i <= lenstr; ++i) addChar(str[i] - 'A', i);
}
char str[maxn * ];
int lenstr;
int in[maxn * ];
int dp[maxn * ];
queue<int> que;
int ans[maxn * ];
char sub[maxn];
int tonext[maxn];
void get_next(char str[], int lenstr) {
    int i = , j = ;
    tonext[] = ;
    while (i <= lenstr) {
        if (j ==  || str[i] == str[j]) {
            tonext[++i] = ++j;
        } else j = tonext[j];
    }
    return;
}
struct node {
    int len;
    LL val;
    bool operator < (const struct node & rhs) const {
        return len < rhs.len;
    }
} out[maxn];
void work() {
    scanf("%s", str + );
    lenstr = strlen(str + );
    build(str, lenstr);
    for (int i = ; i < t; ++i) {
        in[suffixAutomaton[i].fa->id]++;
        if (suffixAutomaton[i].flag) dp[i] = ;
    }
    for (int i = ; i < t; ++i) {
        if (in[i] == ) que.push(i);
    }
    while (!que.empty()) {
        int cur = que.front();
        que.pop();
        if (!cur) break;
        dp[suffixAutomaton[cur].fa->id] += dp[cur];
        in[suffixAutomaton[cur].fa->id]--;
        if (in[suffixAutomaton[cur].fa->id] == ) que.push(suffixAutomaton[cur].fa->id);
    }
    strcpy(sub + , str + );
    int lensub = lenstr;
    int now = ;
    for (int i = ; i <= lensub; ++i) {
        if (suffixAutomaton[now].pNext[sub[i] - 'A']) {
            now = suffixAutomaton[now].pNext[sub[i] - 'A']->id;
            ans[i] = dp[now];
        } else break;
    }
    get_next(str, lenstr);
    int len = ;
    out[len].len = lenstr, out[len].val = ;
    int t = tonext[lenstr + ];
    while (t > ) {
        ++len;
        out[len].len = t - , out[len].val = ans[t - ];
        t = tonext[t];
    }
    printf("%d\n", len);
    for (int i = len; i >= ; --i) {
        printf("%d %I64d\n", out[i].len, out[i].val);
    }
}
int main() {
#ifdef local
    freopen("data.txt", "r", stdin);
//    freopen("data.txt", "w", stdout);
#endif
    work();
    return ;
}

和这题：http://acm.gdufe.edu.cn/Problem/read/id/1338

但是卡STL得queue。不是不是不是，是卡了%I64d的输出，%lld和%d都ac

#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
using namespace std;
#define inf (0x3f3f3f3f)
typedef long long int LL;
const int maxn = 1e6 + , N = ;
struct Node {
    int mxCnt; //mxCnt表示后缀自动机中当前节点识别子串的最大长度
    int miCnt; //miCnt表示后缀自动机中当前节点识别子串的最小长度
    int id; //表示它是第几个后缀自动机节点，指向了它，但是不知道是第几个，用id判断
    int pos; //pos表示它在原串中的位置。
    bool flag; //表示当前节点是否能识别前缀
    struct Node *pNext[N], *fa;
}suffixAutomaton[maxn * ], *root, *last; //大小需要开2倍，因为有一些虚拟节点
int t;  //用到第几个节点
struct Node *create(int mxCnt = -, struct Node *node = NULL) { //新的节点
    if (mxCnt != -) {
        suffixAutomaton[t].mxCnt = mxCnt, suffixAutomaton[t].fa = NULL;
        for (int i = ; i < N; ++i) suffixAutomaton[t].pNext[i] = NULL;
    } else {
        suffixAutomaton[t] = *node; //保留了node节点所有的指向信息
        //可能需要注意下pos，在原串中的位置。现在pos等于原来node的pos
    }
    suffixAutomaton[t].id = t;  //必须要有的，不然id错误
    suffixAutomaton[t].flag = false;
    return &suffixAutomaton[t++];
}
void addChar(int x, int pos) { //pos表示在原串的位置
    struct Node *p = last, *np = create(p->mxCnt + , NULL);
    np->flag = true;
    np->pos = pos, last = np; //last是最尾那个可接收后缀字符的点。
    for (; p != NULL && p->pNext[x] == NULL; p = p->fa) p->pNext[x] = np;
    if (p == NULL) {
        np->fa = root;
        np->miCnt = ; // 从根节点引一条边过来
        return;
    }
    struct Node *q = p->pNext[x];
    if (q->mxCnt == p->mxCnt + ) { //中间没有任何字符
        np->fa = q;
        np->miCnt = q->mxCnt + ; // q是7-->8的那些"ab"，np是"bab"长度是2+1
        return;
    }
    // p： 当前往上爬到的可以接受后缀的节点
    // np：当前插入字符x的新节点
    // q： q = p->pNext[x]，q就是p中指向的x字符的节点
    // nq：因为q->cnt != p->cnt + 1而新建出来的模拟q的节点
    struct Node *nq = create(-, q); // 新的q节点，用来代替q，帮助np接收后缀字符
    nq->mxCnt = p->mxCnt + ; //就是需要这样，这样中间不包含任何字符
    q->miCnt = nq->mxCnt + , np->miCnt = nq->mxCnt + ;
    q->fa = nq, np->fa = nq; //现在nq是包含了本来q的所有指向信息
    for (; p && p->pNext[x] == q; p = p->fa) {
        p->pNext[x] = nq;
    }
}
void init() {
    t = ;
    root = last = create(, NULL);
}
void build(char str[], int lenstr) {
    init();
    for (int i = ; i <= lenstr; ++i) addChar(str[i] - 'A', i);
}
char str[maxn * ];
int lenstr;
int in[maxn * ];
int dp[maxn * ];
int que[maxn * ];
int ans[maxn * ];
char sub[maxn];
int tonext[maxn];
void get_next(char str[], int lenstr) {
    int i = , j = ;
    tonext[] = ;
    while (i <= lenstr) {
        if (j ==  || str[i] == str[j]) {
            tonext[++i] = ++j;
        } else j = tonext[j];
    }
    return;
}
struct node {
    int len;
    int val;
} out[maxn];
void work() {
    scanf("%s", str + );
    lenstr = strlen(str + );
    build(str, lenstr);
    for (int i = ; i < t; ++i) {
        in[suffixAutomaton[i].fa->id]++;
        if (suffixAutomaton[i].flag) dp[i] = ;
    }
    int head = , tail = ;
    for (int i = ; i < t; ++i) {
        if (in[i] == ) que[tail++] = i;
    }
    while (head < tail) {
        int cur = que[head++];
        if (!cur) break;
        dp[suffixAutomaton[cur].fa->id] += dp[cur];
        in[suffixAutomaton[cur].fa->id]--;
        if (in[suffixAutomaton[cur].fa->id] == ) que[tail++] = suffixAutomaton[cur].fa->id;
    }
    int now = ;
    for (int i = ; i <= lenstr; ++i) {
        if (suffixAutomaton[now].pNext[str[i] - 'A']) {
            now = suffixAutomaton[now].pNext[str[i] - 'A']->id;
            ans[i] = dp[now];
        } else break;
    }
    get_next(str, lenstr);
    int len = ;
    out[len].len = lenstr, out[len].val = ;
    int t = tonext[lenstr + ];
    while (t > ) {
        ++len;
        out[len].len = t - , out[len].val = ans[t - ];
        t = tonext[t];
    }
    printf("%d\n", len);
    for (int i = len; i >= ; --i) {
        printf("%d %d\n", out[i].len, out[i].val);
    }
}
int main() {
#ifdef local
    freopen("data.txt", "r", stdin);
//    freopen("data.txt", "w", stdout);
#endif
    work();
    return ;
}

求两个串的最短公共子串，并且出现次数只能是1次

http://www.cnblogs.com/liuweimingcprogram/p/7483425.html

Longest Common Substring II

SPOJ - LCS2

https://vjudge.net/problem/SPOJ-LCS2

求N个串的LCS

这题卡时间卡的好死，1e6的广义后缀自动机被卡了，应该带点常数，被卡了。

#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
using namespace std;
#define inf (0x3f3f3f3f)
typedef long long int LL;
const int MOD = 1e9 + ;
const int maxn = 2e6 + , N = ;
struct Node {
    int mxCnt; //mxCnt表示后缀自动机中当前节点识别子串的最大长度
    int miCnt; //miCnt表示后缀自动机中当前节点识别子串的最小长度
    int id; //表示它是第几个后缀自动机节点，指向了它，但是不知道是第几个，用id判断
    int pos; //pos表示它在原串中的位置。
    bool flag; //表示当前节点是否能识别前缀
    bool R[]; // 广义后缀自动机识别此状态是否在第R[i]个主串中出现过
    struct Node *pNext[N], *fa;
}suffixAutomaton[maxn], *root, *last; //大小需要开2倍，因为有一些虚拟节点
int t;  //用到第几个节点
struct Node *create(int mxCnt = -, struct Node *node = NULL) { //新的节点
    if (mxCnt != -) {
        suffixAutomaton[t].mxCnt = mxCnt, suffixAutomaton[t].fa = NULL;
        for (int i = ; i < N; ++i) suffixAutomaton[t].pNext[i] = NULL;
    } else {
        suffixAutomaton[t] = *node; //保留了node节点所有的指向信息。★全部等于node
        //可能需要注意下pos，在原串中的位置。现在pos等于原来node的pos
    }
    suffixAutomaton[t].id = t;  //必须要有的，不然id错误
    suffixAutomaton[t].flag = false; //默认不是前缀节点
    return &suffixAutomaton[t++];
}
namespace IO
{
const int MT = 7e7;
char buf[MT];
int c, sz;
void begin()
{
    c = ;
    sz = fread(buf, , MT,stdin);
}
inline bool read(int &t)
{
    while (c < sz && buf[c] != '-' &&(buf[c] < '' || buf[c] > '')) c++;
    if (c >= sz) return ;
    bool flag = ;
    if (buf[c] == '-') flag = , c++;
    for (t = ; c < sz && '' <= buf[c] && buf[c] <= '' ; c++) t = t *  + buf[c] - '';
    if (flag) t = -t;
    return ;
}
inline int read(char s[]) {
    while (c < sz && (buf[c] == ' ' || buf[c] == '\n')) c++;
    if (c >= sz) return false;
    int len = ;
    while (c < sz && buf[c] != ' ' && buf[c] != '\n') s[len++] = buf[c], c++;
    s[len] = ;
    return len;
}
}
using namespace IO;
void addChar(int x, int pos, int id) { //pos表示在原串的位置
    struct Node *p = last;
    if (p->pNext[x] != NULL) { // 有了，就不需要np，广义后缀自动机
        struct Node *q = p->pNext[x];
        if (p->mxCnt +  == q->mxCnt) {
            last = q; //用来接收后缀字符
            q->flag = true;
            q->R[id] = true;
            q->pos |=  << pos;
            return;
        }
        //现在的q没办法成为接受后缀的点
        //那么就开一个节点模拟它，所以这个节点是id的前缀节点
        struct Node * nq = create(-, q);
        nq->pos |=  << pos;
        for (int i = ; i < ; ++i) nq->R[i] = false;
        nq->mxCnt = p->mxCnt + ;
        nq->R[id] = true;
        nq->flag = true; //这个点是属于id的。是id的前缀节点，因为q不能接受后缀
        q->fa = nq; //这里是没有np的
        q->miCnt = nq->mxCnt + ;
        for (; p && p->pNext[x] == q; p = p->fa) p->pNext[x] = nq;
        last = nq; //成为接受后缀的节点。
        return;
    }
    struct Node *np = create(p->mxCnt + , NULL);
    for (int i = ; i < ; ++i) np->R[i] = false; //每次都要清空
    np->R[id] = true;
    np->flag = true; //前缀节点
    np->pos =  << pos, last = np; //last是最尾那个可接收后缀字符的点。
    for (; p != NULL && p->pNext[x] == NULL; p = p->fa) p->pNext[x] = np;
    if (p == NULL) {
        np->fa = root;
        np->miCnt = ; // 从根节点引一条边过来
        return;
    }
    struct Node *q = p->pNext[x];
    if (q->mxCnt == p->mxCnt + ) { //中间没有任何字符，可以用来代替接受后缀、
        np->fa = q;
        np->miCnt = q->mxCnt + ; // q是状态8的"ab"，np是状态7的"bab"长度是2+1
        return;
    }
    struct Node *nq = create(-, q); // 新的q节点，用来代替q，帮助np接收后缀字符
    for (int i = ; i < ; ++i) nq->R[i] = false;
    nq->mxCnt = p->mxCnt + ; //就是需要这样，这样中间不包含任何字符
    q->miCnt = nq->mxCnt + , np->miCnt = nq->mxCnt + ;
    q->fa = nq, np->fa = nq; //现在nq是包含了本来q的所有指向信息
    for (; p && p->pNext[x] == q; p = p->fa) {
        p->pNext[x] = nq;
    }
}
void init() {
    t = ;
    root = last = create(, NULL);
}
char str[maxn];
LL dp[maxn][];
queue<int> que;
int in[maxn];
int is[maxn];
void work() {
    begin();
    init();
    int all = ;
    while (read(str + )) {
        last = root;
        for (int i = ; str[i]; ++i) {
            addChar(str[i] - 'a', all, all);
        }
        ++all;
//        printf("%s\n", str + 1);
    }
    for (int i = ; i < t; ++i) {
        in[suffixAutomaton[i].fa->id]++;
        if (suffixAutomaton[i].flag) {
            for (int j = ; j < all; ++j) {
                dp[i][j] = suffixAutomaton[i].R[j];
            }
        }
        is[i] = suffixAutomaton[i].pos;
    }
    for (int i = ; i < t; ++i) {
        if (in[i] == ) {
            que.push(i);
        }
    }
    while (!que.empty()) {
        int cur = que.front();
        que.pop();
        if (!cur) break;
        for (int i = ; i < all; ++i) {
            dp[suffixAutomaton[cur].fa->id][i] += dp[cur][i];
            is[suffixAutomaton[cur].fa->id] |= is[cur];
        }
        in[suffixAutomaton[cur].fa->id]--;
        if (in[suffixAutomaton[cur].fa->id] == ) que.push(suffixAutomaton[cur].fa->id);
    }
    int ans = ;
    for (int i = ; i < t; ++i) {
        if (is[i] == ( << all) - ) {
            ans = max(ans, suffixAutomaton[i].mxCnt);
        }
    }
    cout << ans << endl;
}

int main() {
#ifdef local
    freopen("data.txt", "r", stdin);
//    freopen("data.txt", "w", stdout);
#endif
    work();
    return ;
}

自己想着先用一个串建立sam，然后其他串去爬，求得每个串的每个前缀与第一个串的LCS，然后发现这样不行，每个串的前缀都不同

然后看了下题解，这题是对状态进行搞事，和我上面的思路差不多，但是是记录在sam的每一个状态上，很好。

具体就是，对剩下的串都去sam中求LCS，记录在sam每个节点的信息中，然后N个串的LCS肯定是每个状态的LCS的min值

然后对所有状态进行max即可。

细节：首先假设求LCS大家都懂了。

可以知道的是，加如状态s的LCS值是len，那么fa[s]的LCS值肯定是mxCnt[fa[s]]

mxCnt就是状态能识别子串的最大长度。

因为fa[s]都是s的后缀嘛，所以是必然的。

然后就可以咯，沿着fa更新上去就好，注意如果这个节点有值了的话就可以不需要继续往上爬了，道理很简单，不然TLE

wa点：同一个串，是可以走到同一个状态多次的，因为有可能匹配不成功，然后返回了root那里。

所以走到同一个状态的时候要取max值

#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
using namespace std;
#define inf (0x3f3f3f3f)
typedef long long int LL;
const int maxn = 1e6 + , N = ;
struct SAM {
    int mxCnt[maxn << ], son[maxn << ][N], fa[maxn << ], pos[maxn << ];
//    int flag[maxn << 1][3]; //是否前缀节点
    int flag[maxn << ][];
    int root, last, DFN, t;
    int cmp[maxn << ][];
    int create() {
        ++t;
        for (int i = ; i < ; ++i) cmp[t][i] = ;
        mxCnt[t] = pos[t] = fa[t] = NULL;
        for (int i = ; i < N; ++i) son[t][i] = NULL;
        return t;
    }
    void init() {
        ++DFN;
        t = , root = ;
        last = create();
    }
    void addChar(int x, int _pos, int id) { // _pos表示在原串中的位置
        int p = last;
        int np = create();
        last = np;
        mxCnt[np] = mxCnt[p] + , pos[np] =  << _pos; //前缀节点
        flag[np][id] = DFN;
        for (; p && son[p][x] == NULL; p = fa[p]) son[p][x] = np;
        if (p == NULL) {
            fa[np] = root;
            return;
        }
        int q = son[p][x];
        if (mxCnt[q] == mxCnt[p] + ) {
            fa[np] = q;
            return;
        }
        int nq = create(); //用来代替q的，默认不是前缀节点
        pos[nq] = pos[q]; //pos要和q相同
        for (int i = ; i < N; ++i) son[nq][i] = son[q][i];
        fa[nq] = fa[q], mxCnt[nq] = mxCnt[p] + ;
        fa[q] = nq, fa[np] = nq;
        for (; p && son[p][x] == q; p = fa[p]) son[p][x] = nq;
    }
    int dp[maxn << ][], in[maxn << ], que[maxn << ];
    void topo() {
        for (int i = ; i <= t; ++i) {
            in[fa[i]]++;
            for (int j = ; j < ; ++j) {
                dp[i][j] = flag[i][j] == DFN;
            }
        }
        int head = , tail = ;
        for (int i = ; i <= t; ++i) {
            if (in[i] == ) que[tail++] = i;
        }
        while (head < tail) {
            int cur = que[head++];
            if (cur == root) break;
            pos[fa[cur]] |= pos[cur];
            for (int j = ; j < ; ++j) {
                dp[fa[cur]][j] += dp[cur][j];
            }
            in[fa[cur]]--;
            if (in[fa[cur]] == ) que[tail++] = fa[cur];
        }
    }
} sam;
char str[maxn];
void work() {
    int iii = ;
    while (scanf("%s", str + ) > ) {
        int len = ;
        int now = sam.root;
        for (int i = ; str[i]; ++i) {
            int id = str[i] - 'a';
            if (sam.son[now][id]) {
                now = sam.son[now][id];
                len++;
            } else {
                while (now && !sam.son[now][id]) {
                    now = sam.fa[now];
                }
                if (now == ) {
                    len = , now = sam.root;
                } else {
                    len = sam.mxCnt[now] + ;
                    now = sam.son[now][id];
                }
            }
            sam.cmp[now][iii] = max(len, sam.cmp[now][iii]); //wa点
            int res = now, ttt = now;
            while (res) {
                ttt = res;
                res = sam.fa[res];
                if (sam.cmp[res][iii]) break;
                if (sam.cmp[ttt][iii]) {
                    sam.cmp[res][iii] = sam.mxCnt[res];
                }
            }
        }
        iii++;
    }
    int ans = ;
    for (int i = ; i <= sam.t; ++i) {
        int t = inf;
        for (int j = ; j < iii; ++j) {
            t = min(t, sam.cmp[i][j]);
        }
        ans = max(ans, t);
    }
    printf("%d\n", ans);
}

int main() {
#ifdef local
    freopen("data.txt", "r", stdin);
//    freopen("data.txt", "w", stdout);
#endif
    scanf("%s", str + );
    sam.init();
    for (int i = ; str[i]; ++i) sam.addChar(str[i] - 'a', , );
    work();
    return ;
}

hdu 4416

和上面LCS的那题一样，sam后求出每个状态的最大匹配数量即可

#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
using namespace std;
#define inf (0x3f3f3f3f)
typedef long long int LL;
const int maxn = 1e5 + , N = ;
struct SAM {
    int mxCnt[maxn << ], son[maxn << ][N], fa[maxn << ], pos[maxn << ];
//    int flag[maxn << 1][3]; //是否前缀节点
    int root, last, DFN, t;
    int cmp[maxn << ];
    int create() {
        ++t;
        mxCnt[t] = pos[t] = fa[t] = NULL;
        for (int i = ; i < N; ++i) son[t][i] = NULL;
        return t;
    }
    void init() {
        ++DFN;
        t = , root = ;
        last = create();
    }
    void addChar(int x, int _pos, int id) { // _pos表示在原串中的位置
        int p = last;
        int np = create();
        last = np;
        mxCnt[np] = mxCnt[p] + , pos[np] =  << _pos; //前缀节点
        for (; p && son[p][x] == NULL; p = fa[p]) son[p][x] = np;
        if (p == NULL) {
            fa[np] = root;
            return;
        }
        int q = son[p][x];
        if (mxCnt[q] == mxCnt[p] + ) {
            fa[np] = q;
            return;
        }
        int nq = create(); //用来代替q的，默认不是前缀节点
        pos[nq] = pos[q]; //pos要和q相同
        for (int i = ; i < N; ++i) son[nq][i] = son[q][i];
        fa[nq] = fa[q], mxCnt[nq] = mxCnt[p] + ;
        fa[q] = nq, fa[np] = nq;
        for (; p && son[p][x] == q; p = fa[p]) son[p][x] = nq;
    }
} sam;
char str[maxn];
void work() {
    int n;
    scanf("%d", &n);
    scanf("%s", str + );
    sam.init();
    for (int i = ; str[i]; ++i) sam.addChar(str[i] - 'a', , );
    for (int i = ; i <= sam.t; ++i) {
        sam.cmp[i] = sam.mxCnt[sam.fa[i]];
    }
    for (int i = ; i <= n; ++i) {
        scanf("%s", str + );
        int len = , now = sam.root;
        for (int j = ; str[j]; ++j) {
            int id = str[j] - 'a';
            if (sam.son[now][id]) {
                now = sam.son[now][id];
                len++;
            } else {
                while (now && !sam.son[now][id]) now = sam.fa[now];
                if (now == ) {
                    now = sam.root;
                    len = ;
                } else {
                    len = sam.mxCnt[now] + ;
                    now = sam.son[now][id];
                }
            }
//            printf("%d ", len);
            sam.cmp[now] = max(sam.cmp[now], len);
            int res = now;
            while (sam.fa[res] && sam.cmp[now]) {
                if (sam.cmp[sam.fa[res]] == sam.mxCnt[sam.fa[res]]) break;
                sam.cmp[sam.fa[res]] = sam.mxCnt[sam.fa[res]];
                res = sam.fa[res];
            }
        }
//        printf("\n");
    }
    LL ans = ;
    for (int i = ; i <= sam.t; ++i) {
        ans += sam.mxCnt[i] - sam.cmp[i];
    }
    static int f = ;
    printf("Case %d: %lld\n", ++f, ans);
}

int main() {
#ifdef local
    freopen("data.txt", "r", stdin);
//    freopen("data.txt", "w", stdout);
#endif
    int t;
    scanf("%d", &t);
    while (t--) work();
    return ;
}