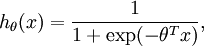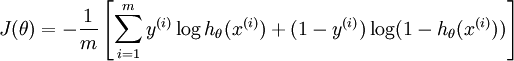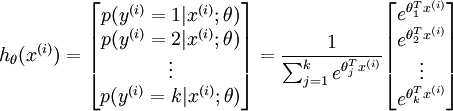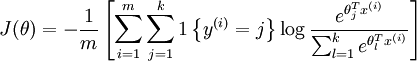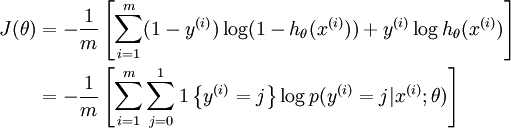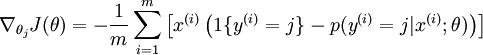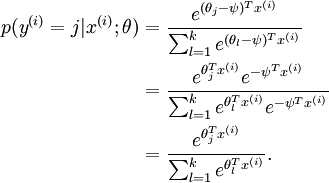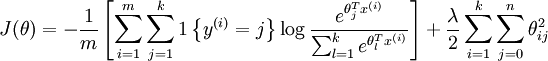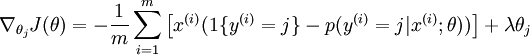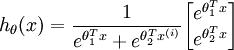softmax与logistic关系
Softmax回归模型,该模型是logistic回归模型在多分类问题上的推广,在多分类问题中,类标签  可以取两个以上的值。 Softmax回归模型对于诸如MNIST手写数字分类等问题是很有用的,该问题的目的是辨识10个不同的单个数字。Softmax回归是有监督的,(译者注: MNIST 是一个手写数字识别库,由NYU 的Yann LeCun 等人维护。http://yann.lecun.com/exdb/mnist/ )
可以取两个以上的值。 Softmax回归模型对于诸如MNIST手写数字分类等问题是很有用的,该问题的目的是辨识10个不同的单个数字。Softmax回归是有监督的,(译者注: MNIST 是一个手写数字识别库,由NYU 的Yann LeCun 等人维护。http://yann.lecun.com/exdb/mnist/ )
回想一下在 logistic 回归中,我们的训练集由 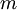 个已标记的样本构成:
个已标记的样本构成: ,其中输入特征
,其中输入特征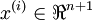 。(我们对符号的约定如下:特征向量
。(我们对符号的约定如下:特征向量  的维度为
的维度为 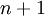 ,其中
,其中 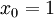 对应截距项 。) 由于 logistic 回归是针对二分类问题的,因此类标记
对应截距项 。) 由于 logistic 回归是针对二分类问题的,因此类标记 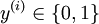 。假设函数(hypothesis function) 如下:
。假设函数(hypothesis function) 如下:
我们将训练模型参数  ,使其能够最小化代价函数 :
,使其能够最小化代价函数 :
在 softmax回归中,我们解决的是多分类问题(相对于 logistic 回归解决的二分类问题),类标  可以取
可以取  个不同的值(而不是 2 个)。因此,对于训练集
个不同的值(而不是 2 个)。因此,对于训练集  ,我们有
,我们有 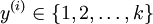 。(注意此处的类别下标从 1 开始,而不是 0)。例如,在 MNIST 数字识别任务中,我们有
。(注意此处的类别下标从 1 开始,而不是 0)。例如,在 MNIST 数字识别任务中,我们有 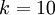 个不同的类别。
个不同的类别。
对于给定的测试输入  ,我们想用假设函数针对每一个类别j估算出概率值
,我们想用假设函数针对每一个类别j估算出概率值 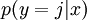 。也就是说,我们想估计
。也就是说,我们想估计  的每一种分类结果出现的概率。因此,我们的假设函数将要输出一个
的每一种分类结果出现的概率。因此,我们的假设函数将要输出一个  维的向量(向量元素的和为1)来表示这
维的向量(向量元素的和为1)来表示这  个估计的概率值。 具体地说,我们的假设函数
个估计的概率值。 具体地说,我们的假设函数 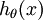 形式如下:
形式如下:
其中 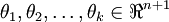 是模型的参数。请注意
是模型的参数。请注意 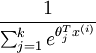 这一项对概率分布进行归一化,使得所有概率之和为 1 。
这一项对概率分布进行归一化,使得所有概率之和为 1 。
为了方便起见,我们同样使用符号  来表示全部的模型参数。在实现Softmax回归时,将
来表示全部的模型参数。在实现Softmax回归时,将  用一个
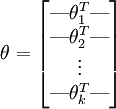
用一个 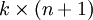 的矩阵来表示会很方便,该矩阵是将
的矩阵来表示会很方便,该矩阵是将 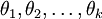 按行罗列起来得到的,如下所示:
按行罗列起来得到的,如下所示:
代价函数
现在我们来介绍 softmax 回归算法的代价函数。在下面的公式中,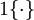 是示性函数,其取值规则为:
是示性函数,其取值规则为:
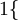
值为真的表达式
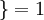
, 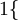 值为假的表达式
值为假的表达式 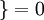 。举例来说,表达式
。举例来说,表达式 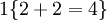 的值为1 ,
的值为1 ,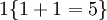 的值为 0。我们的代价函数为:
的值为 0。我们的代价函数为:
值得注意的是,上述公式是logistic回归代价函数的推广。logistic回归代价函数可以改为:
可以看到,Softmax代价函数与logistic 代价函数在形式上非常类似,只是在Softmax损失函数中对类标记的  个可能值进行了累加。注意在Softmax回归中将
个可能值进行了累加。注意在Softmax回归中将  分类为类别
分类为类别  的概率为:
的概率为:
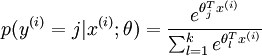 .
.
对于  的最小化问题,目前还没有闭式解法。因此,我们使用迭代的优化算法(例如梯度下降法,或 L-BFGS)。经过求导,我们得到梯度公式如下:
的最小化问题,目前还没有闭式解法。因此,我们使用迭代的优化算法(例如梯度下降法,或 L-BFGS)。经过求导,我们得到梯度公式如下:
让我们来回顾一下符号 "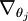 " 的含义。
" 的含义。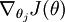 本身是一个向量,它的第
本身是一个向量,它的第  个元素
个元素 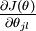 是
是  对
对 的第
的第  个分量的偏导数。
个分量的偏导数。
有了上面的偏导数公式以后,我们就可以将它代入到梯度下降法等算法中,来最小化  。 例如,在梯度下降法的标准实现中,每一次迭代需要进行如下更新:
。 例如,在梯度下降法的标准实现中,每一次迭代需要进行如下更新: 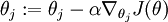 (
(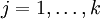 )。
)。
当实现 softmax 回归算法时, 我们通常会使用上述代价函数的一个改进版本。具体来说,就是和权重衰减(weight decay)一起使用。我们接下来介绍使用它的动机和细节。
Softmax回归模型参数化的特点
Softmax 回归有一个不寻常的特点:它有一个“冗余”的参数集。为了便于阐述这一特点,假设我们从参数向量  中减去了向量
中减去了向量  ,这时,每一个
,这时,每一个  都变成了
都变成了 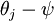 (
(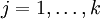 )。此时假设函数变成了以下的式子:
)。此时假设函数变成了以下的式子:
换句话说,从  中减去
中减去  完全不影响假设函数的预测结果!这表明前面的 softmax 回归模型中存在冗余的参数。更正式一点来说, Softmax 模型被过度参数化了。对于任意一个用于拟合数据的假设函数,可以求出多组参数值,这些参数得到的是完全相同的假设函数
完全不影响假设函数的预测结果!这表明前面的 softmax 回归模型中存在冗余的参数。更正式一点来说, Softmax 模型被过度参数化了。对于任意一个用于拟合数据的假设函数,可以求出多组参数值,这些参数得到的是完全相同的假设函数 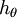 。
。
进一步而言,如果参数 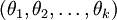 是代价函数
是代价函数  的极小值点,那么
的极小值点,那么 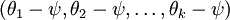 同样也是它的极小值点,其中
同样也是它的极小值点,其中  可以为任意向量。因此使
可以为任意向量。因此使  最小化的解不是唯一的。(有趣的是,由于
最小化的解不是唯一的。(有趣的是,由于  仍然是一个凸函数,因此梯度下降时不会遇到局部最优解的问题。但是 Hessian 矩阵是奇异的/不可逆的,这会直接导致采用牛顿法优化就遇到数值计算的问题)
仍然是一个凸函数,因此梯度下降时不会遇到局部最优解的问题。但是 Hessian 矩阵是奇异的/不可逆的,这会直接导致采用牛顿法优化就遇到数值计算的问题)
注意,当 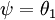 时,我们总是可以将
时,我们总是可以将  替换为
替换为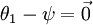 (即替换为全零向量),并且这种变换不会影响假设函数。因此我们可以去掉参数向量
(即替换为全零向量),并且这种变换不会影响假设函数。因此我们可以去掉参数向量  (或者其他
(或者其他  中的任意一个)而不影响假设函数的表达能力。实际上,与其优化全部的
中的任意一个)而不影响假设函数的表达能力。实际上,与其优化全部的 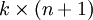 个参数
个参数 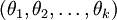 (其中
(其中 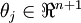 ),我们可以令
),我们可以令 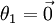 ,只优化剩余的
,只优化剩余的 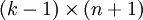 个参数,这样算法依然能够正常工作。
个参数,这样算法依然能够正常工作。
在实际应用中,为了使算法实现更简单清楚,往往保留所有参数 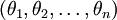 ,而不任意地将某一参数设置为 0。但此时我们需要对代价函数做一个改动:加入权重衰减。权重衰减可以解决 softmax 回归的参数冗余所带来的数值问题。
,而不任意地将某一参数设置为 0。但此时我们需要对代价函数做一个改动:加入权重衰减。权重衰减可以解决 softmax 回归的参数冗余所带来的数值问题。
权重衰减
我们通过添加一个权重衰减项 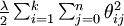 来修改代价函数,这个衰减项会惩罚过大的参数值,现在我们的代价函数变为:
来修改代价函数,这个衰减项会惩罚过大的参数值,现在我们的代价函数变为:
有了这个权重衰减项以后 (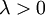 ),代价函数就变成了严格的凸函数,这样就可以保证得到唯一的解了。 此时的 Hessian矩阵变为可逆矩阵,并且因为
),代价函数就变成了严格的凸函数,这样就可以保证得到唯一的解了。 此时的 Hessian矩阵变为可逆矩阵,并且因为 是凸函数,梯度下降法和 L-BFGS 等算法可以保证收敛到全局最优解。
是凸函数,梯度下降法和 L-BFGS 等算法可以保证收敛到全局最优解。
为了使用优化算法,我们需要求得这个新函数  的导数,如下:
的导数,如下:
通过最小化  ,我们就能实现一个可用的 softmax 回归模型。
,我们就能实现一个可用的 softmax 回归模型。
Softmax回归与Logistic 回归的关系
当类别数 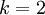 时,softmax 回归退化为 logistic 回归。这表明 softmax 回归是 logistic 回归的一般形式。具体地说,当
时,softmax 回归退化为 logistic 回归。这表明 softmax 回归是 logistic 回归的一般形式。具体地说,当 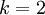 时,softmax 回归的假设函数为:
时,softmax 回归的假设函数为:
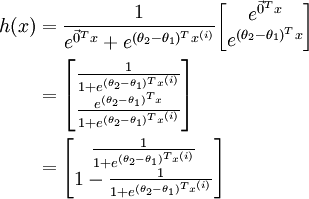
利用softmax回归参数冗余的特点,我们令 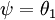 ,并且从两个参数向量中都减去向量
,并且从两个参数向量中都减去向量  ,得到:
,得到:
因此,用 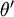 来表示
来表示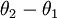 ,我们就会发现 softmax 回归器预测其中一个类别的概率为
,我们就会发现 softmax 回归器预测其中一个类别的概率为 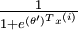 ,另一个类别概率的为
,另一个类别概率的为 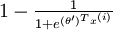 ,这与 logistic回归是一致的。
,这与 logistic回归是一致的。
Softmax 回归 vs. k 个二元分类器
如果你在开发一个音乐分类的应用,需要对k种类型的音乐进行识别,那么是选择使用 softmax 分类器呢,还是使用 logistic 回归算法建立 k 个独立的二元分类器呢?
这一选择取决于你的类别之间是否互斥,例如,如果你有四个类别的音乐,分别为:古典音乐、乡村音乐、摇滚乐和爵士乐,那么你可以假设每个训练样本只会被打上一个标签(即:一首歌只能属于这四种音乐类型的其中一种),此时你应该使用类别数 k = 4 的softmax回归。(如果在你的数据集中,有的歌曲不属于以上四类的其中任何一类,那么你可以添加一个“其他类”,并将类别数 k 设为5。)
如果你的四个类别如下:人声音乐、舞曲、影视原声、流行歌曲,那么这些类别之间并不是互斥的。例如:一首歌曲可以来源于影视原声,同时也包含人声 。这种情况下,使用4个二分类的 logistic 回归分类器更为合适。这样,对于每个新的音乐作品 ,我们的算法可以分别判断它是否属于各个类别。
现在我们来看一个计算视觉领域的例子,你的任务是将图像分到三个不同类别中。(i) 假设这三个类别分别是:室内场景、户外城区场景、户外荒野场景。你会使用sofmax回归还是 3个logistic 回归分类器呢? (ii) 现在假设这三个类别分别是室内场景、黑白图片、包含人物的图片,你又会选择 softmax 回归还是多个 logistic 回归分类器呢?
在第一个例子中,三个类别是互斥的,因此更适于选择softmax回归分类器 。而在第二个例子中,建立三个独立的 logistic回归分类器更加合适。
摘取自:http://ufldl.stanford.edu/wiki/index.php/Softmax回归#Softmax.E5.9B.9E.E5.BD.92.E4.B8.8ELogistic_.E5.9B.9E.E5.BD.92.E7.9A.84.E5.85.B3.E7.B3.BB
softmax与logistic关系的更多相关文章
- 逻辑回归与神经网络还有Softmax regression的关系与区别
本文讨论的关键词:Logistic Regression(逻辑回归).Neural Networks(神经网络) 之前在学习LR和NN的时候,一直对它们独立学习思考,就简单当做是机器学习中的两个不同的 ...
- 【机器学习】Softmax 和Logistic Regression回归Sigmod
二分类问题Sigmod 在 logistic 回归中,我们的训练集由 个已标记的样本构成: ,其中输入特征.(我们对符号的约定如下:特征向量 的维度为 ,其中 对应截距项 .) 由于 logis ...
- Softmax回归——logistic回归模型在多分类问题上的推广
Softmax回归 Contents [hide] 1 简介 2 代价函数 3 Softmax回归模型参数化的特点 4 权重衰减 5 Softmax回归与Logistic 回归的关系 6 Softma ...
- Logistic回归(逻辑回归)和softmax回归
一.Logistic回归 Logistic回归(Logistic Regression,简称LR)是一种常用的处理二类分类问题的模型. 在二类分类问题中,把因变量y可能属于的两个类分别称为负类和正类, ...
- 线性回归、Logistic回归、Softmax回归
线性回归(Linear Regression) 什么是回归? 给定一些数据,{(x1,y1),(x2,y2)…(xn,yn) },x的值来预测y的值,通常地,y的值是连续的就是回归问题,y的值是离散的 ...
- 1.线性回归、Logistic回归、Softmax回归
本次回归章节的思维导图版总结已经总结完毕,但自我感觉不甚理想.不知道是模型太简单还是由于自己本身的原因,总结出来的东西感觉很少,好像知识点都覆盖上了,但乍一看,好像又什么都没有.不管怎样,算是一次尝试 ...
- logistic回归和最大熵
回顾发现,李航的<统计学习方法>有些章节还没看完,为了记录,特意再水一文. 0 - logistic分布 如<统计学习方法>书上,设X是连续随机变量,X服从logistic分布 ...
- Python机器学习笔记 Logistic Regression
Logistic回归公式推导和代码实现 1,引言 logistic回归是机器学习中最常用最经典的分类方法之一,有人称之为逻辑回归或者逻辑斯蒂回归.虽然他称为回归模型,但是却处理的是分类问题,这主要是因 ...
- 【分类器】感知机+线性回归+逻辑斯蒂回归+softmax回归
一.感知机 详细参考:https://blog.csdn.net/wodeai1235/article/details/54755735 1.模型和图像: 2.数学定义推导和优化: 3.流程 ...
随机推荐
- [小问题笔记(一)] js关闭页面window.close() 无效,不弹提示直接关闭
window.close(); 单独写这句,各个浏览器效果都不一样.比如IE(不是所有版本)会弹提示: 点确定之后才会关闭.而有些浏览器压根就没反应. 需要让它不弹提示,直接关闭,在window.cl ...
- 使用MessageFormat替换字符中的占位符
使用String.format可以实现字符串的格式化功能,即将后面参数中的值替换掉format中的%s,%d这些值.但MessageFormat更为强大,不用管传入值是字符串还是数字,使用占位符即可. ...
- Angular2-使用Augury来调试Angular2程序
参考: http://www.jianshu.com/p/efecaea287f2https://augury.angular.io/ https://augury.angular.io/pages/ ...
- [Spring]Spring Mvc实现国际化/多语言
1.添加多语言文件*.properties F64_en_EN.properties详情如下: F60_G00_M100=Please select data. F60_G00_M101=Are yo ...
- Dubbo 和 Spring Cloud微服务架构 比较及相关差异
你真的了解微服务架构吗?听听八年阿里架构师怎样讲述Dubbo和Spring Cloud微服务架构. 微服务架构是互联网很热门的话题,是互联网技术发展的必然结果.它提倡将单一应用程序划分成一组小的服务, ...
- The tilde ( ~ ) operator in JavaScript
From the JavaScript Reference on MDC, ~ (Bitwise NOT) Performs the NOT operator on each bit. NOT a y ...
- 【Python】高阶函数介绍
其实函数可以作为变量,之前学过C++,对于这种用法并不奇怪.无非就是函数充当变量,可以传入函数而已. 下面分别介绍 Python 中常见的高阶函数:map/reduce, filter, sorted ...
- 1.spring cloud eureka server配置
IDEA版本 2017.2.5 JDK 1.8 红色加粗内容为修改部分 1.创建一个新项目 2.选择eureka依赖 3.版本选择(重要)并且更新依赖 <?xml version="1 ...
- ActiveMQ教程(消息发送和接受)
一 环境的搭建 version为你的版本号 如果你是普通的项目的话,创建一个lib文件夹,导入相应的jar包到你的lib中,jar包为:activemq-all-{version}.jar.log4j ...
- C++复习15.指针知识
C++复习15.指针知识 4.指针知识 在Tencent 笔试和面试中都考到了 C/C++中的指针知识,因为自己很不喜欢使用指针,所以才开始学习 Java的,但是现在看来还是躲不掉的,所 ...