[图解算法] 归并排序MergeSort——<递归与分治策略>

 #include"iostream.h"
 void Merge(int c[],int d[],int l,int m,int r){
     int i=l,j=m+,k=l;
     while((i<=m)&&(j<=r)){//循环两组中较小者先放入d[]暂存
         if(c[i]<=c[j]) d[k++]=c[i++];
         else d[k++]=c[j++];
     }
     if(i>m) for(int q=j;q<=r;q++) d[k++]=c[q];
     else for(int q=i;q<=m;q++) d[k++]=c[q];
 }

 void MergePass(int x[],int y[],int s,int n){
     int i=;
     while(i<=n-*s){
         Merge(x,y,i,i+s-,i+*s-);
         i=i+*s;
     }
     if(i+s<n) Merge(x,y,i,i+s-,n-);
     else for(int j=i;j<=n-;j++) y[j]=x[j];
 }

 void MergeSort(int a[],int n){
     int* b=new int[n];
     int s=;
     while(s<n){
         MergePass(a,b,s,n);
         s+=s;
         MergePass(b,a,s,n);
         s+=s;
     }
 }

 void main(){
     int a[] = {,,,,,,,,,};
     int size = sizeof(a)/sizeof(int);
     MergeSort(a,size+);
     for(int i=;i<size;++i)
         cout<<a[i]<<",";
     cout<<endl;
 }

注：文末有GIF动图解析。以上代码复制放入VC6可使用。

[图解+例子]

一、建立数组

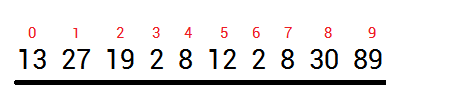（共10个随机乱序数）

二、设置拆分规模

MergeSort(int a[],int n)

把数组a[]及其长度n传入，并设置规模s为1（其实就是设置多少个数放一起排序啦，没那么高大上），即从一个和一个元素比较开始，每调用一次MergePass()，s翻倍。

三、拆分数组

MergePass(int x[],int y[],int s,int n)

遍历数组直到i比n-2*s大

（为什么是n-2s不是n？答：留个“尾巴”单独处理，比如四个数四个数合并，总共有10个数，剩下两个需要单独处理）

【对s的解释：规模s为上一次的规模，即构成新组的，如两个组合并，每个组1个元素，产生2个数的新组，此时规模s为1】

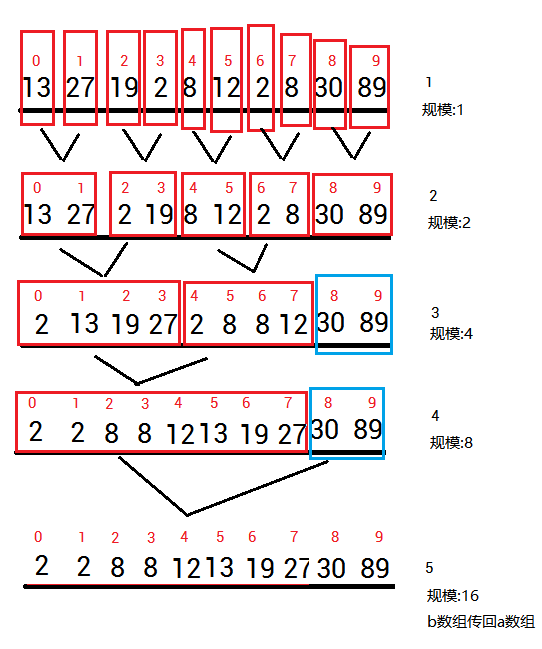
第一步1个1个合并成一个含2个元素的有序组s=1；

第二步2个2个合并成一个含4个元素的有序组s=2；

第三步4个4个合并成一个含8个元素的有序组s=4，

此时情况出现特殊，既然是合并成8个，意味着只要符合每8个有序就可以了，所以剩下两个是属于后8个，但是实际上剩余6个空位（见第四步图）

于是有了开头的判断“尾巴”的以下语句：

if (i+s<n) Merge(x,y,i,i+s-1,n-1);  //如果多出来的尾巴比s要长(n-i>s)证明上一次规模的排序不足以把“尾巴”全部排有序
else for(int j=i;j<=n-1;j++) y[j]=x[j];   //如果多出来的尾巴比s要短或等于(n-i<=s)证明上一次规模的排序已经排好了尾巴

显然我们剩下两个元素刚好等于上一次规模s=2，所以属于第二种情况，已经排好了尾巴直接把它存入数组。

所以现在是8+8的有序数组，期中后面的8只有两个元素，也就引出了第四步。

第四步8个8个合并成一个含16个元素的有序组s=8，

显然，此时规模s为8，符合判断“尾巴”的第一种情况，尾巴比8长，所以调用merge()处理两组数据（如下图）。

有人可能会问，尾巴不是2吗？

不

尾巴此时为10。

因为规模为8的时候，需要两对8个数，才可以算一组，所以s=8时的尾巴应该是n%16，不是n%8

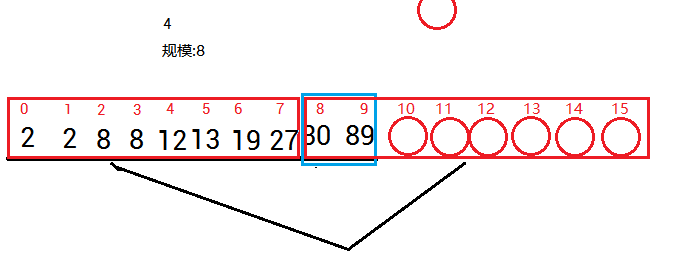
当然，总的个数就10个，后面红圈只是方便理解添加的。

第五步16个16个合并成一个含32个元素的有序组s=16，

s1=2 s2=4;

s3=8 s4=16;

为了保证数组传回a，s应当成对存在，所以第五步实际并没合并，只是把数组b传回数组a了

不断的拆->结合

递归->合并

分治问题->解决问题

。。。

四、解决子问题

Merge(int c[],int d[],int l,int m,int r)

此函数即为归并中并的操作，也是整个归并里的最基本的函数，用来处理各组的合并。

举个栗子：

a[0:3] : 2 3 19 27与a[4:7] 2 8 8 12合并

a[0]和a[4]比较，2=2放a[0]进暂存数组b，

a[1]和a[4]比较，3>2放a[4]进暂存数组b，

a[2]和a[4]比较，3<8放a[2]进暂存数组b，

。。。一直放完一方，再把剩下的全加入数组b尾部

得到递增数组b[]。

由于较为简单，此处不再深入解析。其实是困了要睡觉了。。。。。。。。写到半夜。。。

[GIF解析](图源网络，不是上面讲解所用数组)

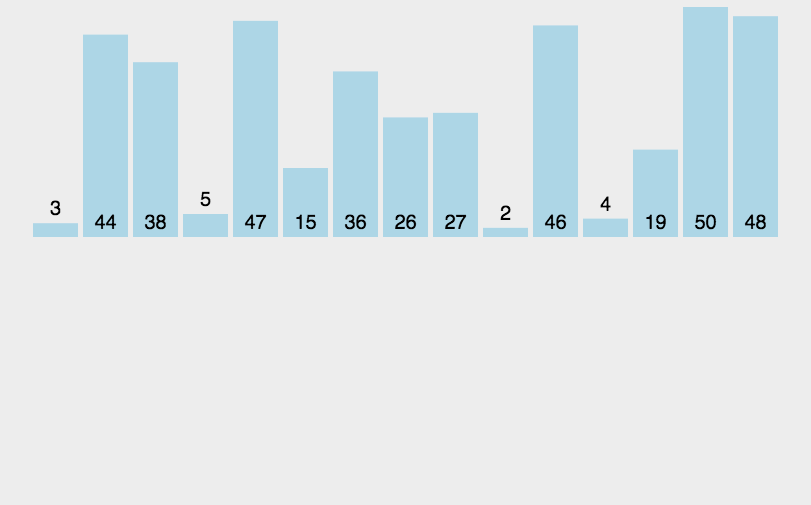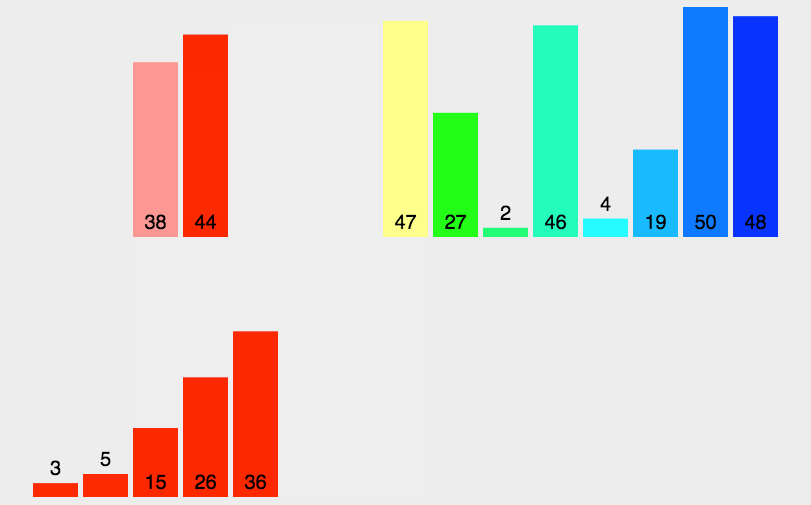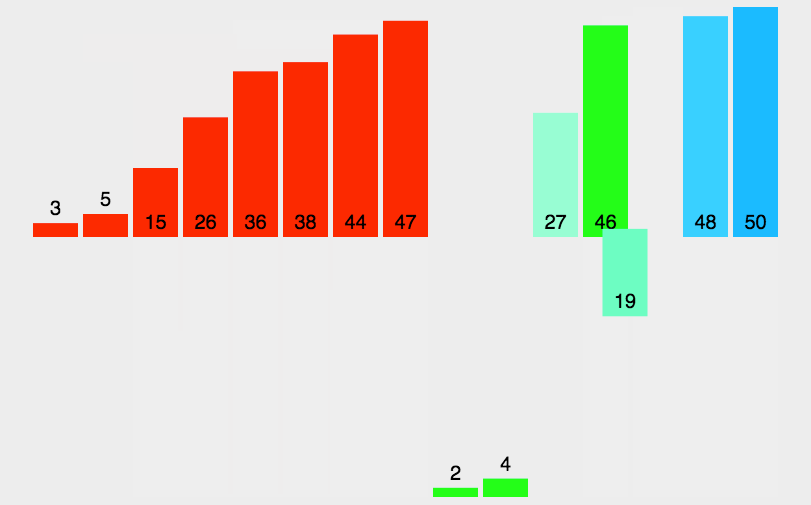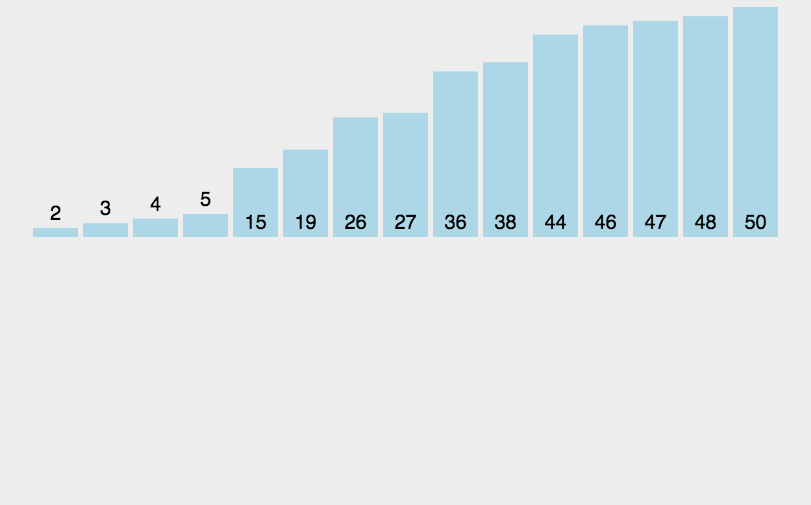
[特例]

有空更新。。。

[总结]

这样通过先递归的分解数列，再合并数列就完成了归并排序！

欢迎一起探讨，本人保留解析著作权。

算法引用自 王晓东. 计算机算法设计与分析[M]. 电子工业出版社, 2012.