Linux nethack
一、简介
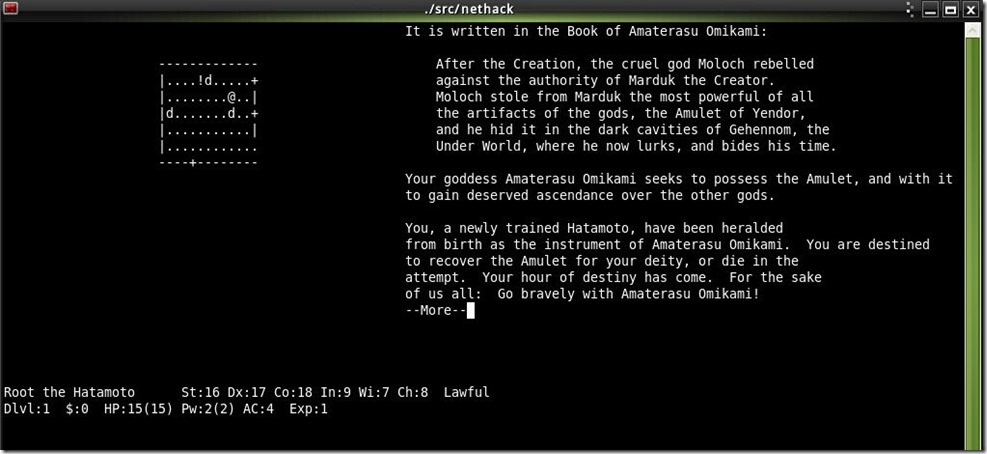
游戏目标：在地下城的最底层取得炎多的护符项链（Amulet of Yendor），并返回最上层，在圣祭坛上供奉给神灵。完成整个游戏的奖赏是，玩家会成为不朽的半神。
二、安装
1）下载源码
2）编译安装
cd $Top/sys/unix
sh setup.sh hints/NAME_OF_HINTS_FILE
cd ../..
make all
make install
三、操作
Linux nethack的更多相关文章
- Linux 驱动开发
linux驱动开发总结(一) 基础性总结 1, linux驱动一般分为3大类: * 字符设备 * 块设备 * 网络设备 2, 开发环境构建: * 交叉工具链构建 * NFS和tftp服务器安装 3, ...
- 28个Unix/Linux的命令行神器_转
28个Unix/Linux的命令行神器 下面是Kristóf Kovács收集的28个Unix/Linux下的28个命令行下的工具,有一些是大家熟悉的,有一些是非常有用的,有一些是不为人知的.这些工具 ...
- 28 个必备的 Linux 命令行工具
dstat & sar iostat, vmstat, ifstat and much more in one. slurm 网络流量图形化工具 vim & emacs 这个没人不知道 ...
- 28个Unix/Linux的命令行神器
下面是Kristóf Kovács收集的28个Unix/Linux下的28个命令行下的工具(原文链接),有一些是大家熟悉的,有一些是非常有用的,有一些是不为人知的.这些工具都非常不错,希望每个人都知道 ...
- 28 个 Unix/Linux 的命令行神器
28 个 Unix/Linux 的命令行神器 下面是Kristóf Kovács收集的28个Unix/Linux下的28个命令行下的工具(原文链接),有一些是大家熟悉的,有一些是非常有用的,有一些 ...
- 我所使用的Linux软件集合
自从2003-2004春节之际初次尝试使用Linux以来,至今已十年有余了.尤其是整个博士研究期间,坚持在Linux下开展学习与研究工作,前前后后试用了不少桌面环境.窗口管理器.终端程序以及其他应用软 ...
- [daily][archlinux][game] 几个linux下还不错的游戏
春节在家放松, 装了几个游戏在archlinux上,玩起来还不错. 假期结束开工了, 玩的时间也会比较少,准备删掉, 记录如下: 1. 0ad 即时战略类, 类似于冷兵器时代的红警. 画面还不错, 可 ...
- 【转】28个Unix/Linux的命令行神器
下面是Kristóf Kovács收集的28个Unix/Linux下的28个命令行下的工具(原文链接),有一些是大家熟悉的,有一些是非常有用的,有一些是不为人知的.这些工具都非常不错,希望每个人都知道 ...
- 转-Linux启动过程详解（inittab、rc.sysinit、rcX.d、rc.local）
http://blog.chinaunix.net/space.php?uid=10167808&do=blog&id=26042 1)BIOS自检2)启动Grub/Lilo3)加 ...
随机推荐
- DbEntry 访问Access2010数据库
在用DbEntry访问Access2010的时候报错如下: 未在本地计算机上注册“Microsoft.ACE.OLEDB.12.0”提供程序 解决方案: 安装AccessDatabaseEngine组 ...
- 转载Verilog乘法器
1. 串行乘法器 两个N位二进制数x.y的乘积用简单的方法计算就是利用移位操作来实现. module multi_CX(clk, x, y, result); input clk; input [7: ...
- flask+mongodb开发restful API
Mac上安装mongodb 的方法:http://www.cnblogs.com/junqilian/p/4109580.html 实现博客的步骤 详细讲解步骤:https://blog.igevin ...
- mysql安装问题汇总
操作系统:win7 mysql版本号:mysql 5.5(64位) 1.又一次安装mysql卡在最后一步过不去 问题描写叙述:第一次安装完mysql.使用jdbc写入的中文都是乱码.但已存在于数据库中 ...
- Android 比对APK的签名信息
https://www.jianshu.com/p/8583f6a966e2 在做App的时候经常会有验证apk是否为正版的需求,比如一些接入第三方支付的app,接入微信sdk也是需要apk签名信息的 ...
- 【HTML5】Canvas绘图详解-1
----->Canvas绘制基础 1,线条绘制 1-1,线条组成的图形和beginPath 案例:绘制由不同颜色的线条组成的图案 1-2,多边形的填充和closePath 案例:绘制封闭具有填充 ...
- 管理11gRAC基本命令 (转载) 很详细
在 Oracle Clusterware 11g 第 2 版 (11.2) 中,有许多子程序和命令已不再使用: crs_stat crs_register crs_unregiste ...
- 1.使用Fiddler进行接口测试
1.Fiddler既可以用来抓包数据,亦可以进行接口测试.(可参考我的另一篇博客:https://www.cnblogs.com/android-it/p/9523548.html 进行接口的编写) ...
- laravel中好用的支付安装包
是包括支付宝和微信的支付 准用包,在测试中 https://github.com/yansongda/laravel-pay 这个包,看上去很好但是composer require时,要求php太高, ...
- 自定义第三方YUM源
1.切换到cloudboot系统目录中 2.拷贝repodata目录的*-repo.xml文件到系统目录下 3.删除系统目录的repodata目录 4.编辑repo.xml内容,base添加rpm包包 ...