【赛时总结】NOIP2018-三校联考1024

◇NOIP三校联考-1024◇

发现以前的博客写得似乎都很水……基本上都没什么阅读量QwQ 决定改过自新╰(￣ω￣ｏ) 就从这篇博客开始吧~

现场考得无地自容，看到题解才发现一些东西……（我第三题还没有做出来，反正做出来再补上）

---

◊ 题目& 简单解析

第一题：组合

【题目】

有n条线段，线段的两端点各有一个值（线段两端值可以相同，也可以存在端点值相同的多条线段）。如果线段A的端点的值为(a,b)，线段B的端点的值为(b,c)，则可以通过将A,B相接，使AB构成一条端点值为(a,c)的线段。求是否存在一种按顺序连接线段的方案，使得所有线段连成一条线段。

另外给出一个参数T，如果T=1，则可以将线段调转方向，即线段 (a,b) 可以看成 (b,a)；如果T=2，则线段不能调转方向。

输入：第一行给出T和n,m，n表示线段端点的值∈[1,n]，m表示共有m条线段；接下来m行每行描述一条线段(a[i],b[i])

输出：第一行输出"YES"/"NO"表示是否存在方案；若为"YES"输出任意一组方案（按连接顺序输出线段编号，若线段连接时调转方向，则输出其编号的相反数）。

【分析】

由于每条线段只能使用一次且必须使用，但是端点值可以重复多次，若将线段(a,b)看作连接a,b的边，则问题转变为求一条欧拉路径（不一定是欧拉环），而T描述的是边是有向边还是无向边（可调转方向则是无向边）。根据欧拉路径的性质——若为无向图，则度数为奇数的点的个数不能超过2，如果存在度数为奇数的点，则必须以某一个度数为奇数的点作为欧拉路径；若为有向图，则出度不等于入度的点的个数不能超过2，且如果存在入度大于出度的点，则必须以该点作为欧拉路径的起点。

根据上述特征先建图。然后判断点的度数，同时确定起点（如果无法找到起点，即上述的两种特殊情况都不存在，则形成的是欧拉回路，所以可以将任意一点作为起点(注意不要直接把1作为起点，因为数据并没有保证点1~n都出现过) 本地检测的时候SpecialJudge写得丑，然后检测器碰到这种情况自己炸了(lll￢ω￢)）。然后就用到了我考试过后才学的Hierholzer算法，专门拿来求欧拉路径/欧拉回路——如果图上存在欧拉回路，则求得的就是欧拉回路，否则求得的是欧拉路径。

Hierholzer算法大概就是从欧拉路径的起点出发，DFS选择一条没有走过的边继续走，直到不能走（没有边或者边都走过）为止，当DFS回溯时，将该边入栈。最后将栈内的所有边出栈就可以得到一条欧拉路径。

当然这样求到的是图中最大的一条欧拉路径，如果欧拉路径的边数没有达到m，即没有走过图中所有的边，则输出"NO"；比如 (↔表示连接)"1↔2，2↔1，3↔4，4↔3"显然无法走完整个图。

第二题：统计

【题目】

给出一个长度为n的序列a[i]，对序列进行m次操作，每次操作指定一个下标i∈(1,n)，对于每一个j | j≥i且a[j]≤a[i] ，将a[j]从原数组中提出（原数组中a[j]的位置留空），再对所有满足条件的a[j]单独排序，最后按顺序放入原数组的空位中。问在操作前和进行操作后数组中逆序对的数量。

eg: a = {1,3,4,2,6,1} →  (i=2) →  a[j] = {3(a[2]),2(a[4]),1(a[6])} →  排序 →  a[j]={1,2,3} →  放入空位 →  a = {1,1,4,2,6,3}

【分析】

众所周知，求逆序对除了用归并排序，还可以用树状数组。根据树状数组，我们可以求出f[i]，表示在i后面的小于a[i]的数的个数（即倒序从n到1插入a[i]，再询问小于a[i]的数的个数）。设操作中被选中的元素的下标集合为 pos（pos升序排列），则对于 j∈pos ，以a[j]作为较大值的逆序对仅存在 ( a[j] , a[k]|k∈pos且k>j ) ，应该很好理解吧，就不多做解释了。因此在对a[j]排序后，对于每一个 i∈pos，就不存在以a[i]为较大值的逆序对了。因此它对答案的贡献就减少了f[i]，但是它的改变不会对以其他元素为较大值的逆序对的数量产生影响。

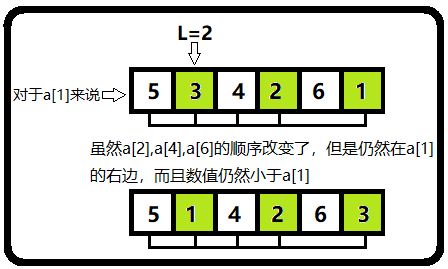
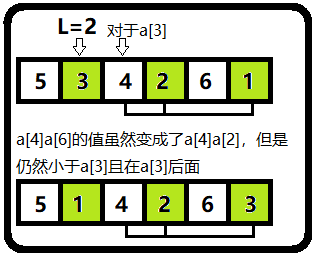
为什么不产生影响？做一个简单的解释：假设选中a[j]的j的最小值为L。

①对于L之前的数a[i]，a[j]排序后仍然在a[i]的后面，且a[i]与a[j]的相对大小没有改变，因此数量不会改变；

②对于L~n之间的数a[i]，满足 a[i]>a[j]（操作的要求），虽然排序后a[j]的位置改变，但是仍然小于a[i]，且数目不变，因此数量不会改变；

举个例子：

好了，扯到贡献了。那么就相当于每次操作后，被操作的a[j]对逆序对的贡献（以a[j]为较大值的逆序对的数量）就变为0了。可以看成把a[j]删除，但是只是删去a[j]的贡献，而在统计其他数的逆序对的时候需要统计a[j]。记最初序列中逆序对的数量为sum，那么我们每进行一次操作，就需要执行 sum-=f[j]（减去a[j]的贡献），顺便删除a[j]。

删除？双向链表！从选中的下标i出发，按链表顺序遍历j，如果a[j]<=a[i]，则将j的前驱接上j的后继（删除），将sum-=f[j]，给f[j]赋值为0。感觉是正解对吧 QwQ？然后就发现被某chuichui tly加的一组特殊数据卡掉了……%%%

无奈写正解，好吧，其实是线段树！用线段树维护区间最小值——如果区间[i,n]的最小值都大于a[i]的话，那么这个区间就不需要操作，否则查找子区间，直到找到叶节点，就找到了小于等于a[i]的a[j]，然后将a[j]改为INF，sum-=f[j]。这样虽然和链表的思路是一样的……但是时间复杂度就由 O(n) 变成了 O(log n)！挺优秀的……(●'◡'●)

（第三题还没做出来，太弱了……好了好了，粘代码了）

---

◊ 源代码

【第一题-merge】

/*Lucky_Glass*/
#include<bits/stdc++.h>
using namespace std;
const int N=int(2e5),M=int(1e5);
int tag,m,n,beg,cnt;
int tot[M+5],ans[N+5];
bool vis[N+5];
struct LINK{int v,id;};
vector< LINK > lnk[M+5];
void DFS(int u,int id){
	for(int i=0;i<(int)lnk[u].size();i++)
		if(!vis[abs(lnk[u][i].id)]){
			vis[abs(lnk[u][i].id)]=true;
			DFS(lnk[u][i].v,lnk[u][i].id);
		}
	if(id) ans[++ans[0]]=id;
}
int main(){
	freopen("merge.in","r",stdin);
	freopen("merge.out","w",stdout);
	scanf("%d%d%d",&tag,&m,&n);
	if(tag==1){
		for(int i=1;i<=n;i++){
			int u,v;scanf("%d%d",&u,&v);beg=u;
			tot[u]^=1;tot[v]^=1;
			lnk[u].push_back((LINK){v,i});
			lnk[v].push_back((LINK){u,-i});
		}
		for(int i=1;i<=m;i++)
			if(tot[i])
				cnt++,beg=i;
		if(cnt>2)
			printf("NO\n"),exit(0);
		DFS(beg,0);
	}
	else{
		for(int i=1;i<=n;i++){
			int u,v;scanf("%d%d",&u,&v);beg=v;
			lnk[u].push_back((LINK){v,i});
			tot[u]++;tot[v]--;
		}
		for(int i=1;i<=m;i++){
			if(tot[i]){
				cnt++;
				if(tot[i]==1) beg=i;
			}
		}
		if(cnt>2)
			printf("NO\n"),exit(0);
		DFS(beg,0);
	}
	if(ans[0]!=n)
		printf("NO\n"),exit(0);
	printf("YES\n");
	for(int i=ans[0];i>=1;i--)
		if(i==1) printf("%d",ans[i]);
		else printf("%d ",ans[i]);
	printf("\n");
	return 0;
}

【第二题（原始数据）-count】

/*Lucky_Glass*/
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) (x&-x)
const int N=2e5;
int n,m;
long long sum;
int tre[N+5],num[N+5],fal[N+5],pre[N+5],beh[N+5];
void Insert(int pos){
	while(pos<=n)
		tre[pos]++,
		pos+=lowbit(pos);
}
int Query(int pos){
	int ret=0;
	while(pos)
		ret+=tre[pos],
		pos-=lowbit(pos);
	return ret;
}
int main(){
	freopen("count.in","r",stdin);
	freopen("count.out","w",stdout);
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%d",&num[i]);
		pre[i]=i-1;
		beh[i]=i+1;
	}
	for(int i=n;i>=1;i--){
		fal[i]=Query(num[i]-1);
		sum+=fal[i];
		Insert(num[i]);
	}
	printf("%lld",sum);
	for(int i=1;i<=m;i++){
		int pos;scanf("%d",&pos);
		if(!fal[pos]){
			printf(" %lld",sum);
			continue;
		}
		for(int j=pos;j<=n;j=beh[j])
			if(num[j]<=num[pos]){
				beh[pre[j]]=beh[j];
				pre[beh[j]]=pre[j];
				sum-=fal[j];
				fal[j]=0;
			}
		printf(" %lld",sum);
	}
	printf("\n");
	return 0;
}

　　

【第二题（额外数据）-count】

/*Lucky_Glass*/
#include<bits/stdc++.h>
using namespace std;
const int N=2e5;
struct TREEARRAY{
	#define lowbit(x) (x&-x)
	int tre[N+5];
	TREEARRAY(){memset(tre,0,sizeof tre);}
	void Insert(int pos,int n){
		while(pos<=n)
			tre[pos]++,
			pos+=lowbit(pos);
	}
	int Query(int pos){
		int ret=0;
		while(pos)
			ret+=tre[pos],
			pos-=lowbit(pos);
		return ret;
	}
}ary;
struct SEGTREE{
	struct NODE{
		int l,r,num;
	}tre[N*5];
	void Update(int u){
		tre[u].num=min(tre[u<<1].num,tre[u<<1|1].num);
	}
	void Init(int a[],int l,int r,int u){
		tre[u].l=l;tre[u].r=r;
		if(l==r){
			tre[u].num=a[l];
			return;
		}
		int mid=(l+r)>>1;
		Init(a,l,mid,u<<1);Init(a,mid+1,r,u<<1|1);
		Update(u);
	}
	void Query(int u,int l,int val,long long &sum,int f[]){
		if(tre[u].r<l || tre[u].num>val) return;
		if(tre[u].l==tre[u].r){
			sum-=f[tre[u].l],tre[u].num=(1<<29);
			return;
		}
		int mid=(tre[u].l+tre[u].r)>>1;
		if(l>=mid+1) Query(u<<1|1,l,val,sum,f);
		else{
			Query(u<<1,l,val,sum,f);
			Query(u<<1|1,l,val,sum,f);
		}
		Update(u);
	}
}seg;
int n,m;
long long sum;
int f[N+5],num[N+5];
int main(){
	freopen("count.in","r",stdin);
	freopen("count.out","w",stdout);
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
		scanf("%d",&num[i]);
	for(int i=n;i>=1;i--){
		sum+=(f[i]=ary.Query(num[i]-1));
		ary.Insert(num[i],n);
	}
	seg.Init(num,1,n,1);
	printf("%lld",sum);
	for(int i=1;i<=m;i++){
		int pos;scanf("%d",&pos);
		seg.Query(1,pos,num[pos],sum,f);
		printf(" %lld",sum);
	}
	return 0;
}

　　

---

The End

Thanks for reading!

- Lucky_Glass

（Tab：如果我有没讲清楚的地方可以直接在邮箱lucky_glass@foxmail.com email我，在周末我会尽量解答并完善博客~）