搜索5--noi1700:八皇后问题

搜索5--noi1700:八皇后问题

一、心得

二、题目

1700:八皇后问题

• 查看
• 提交
• 统计
• 提问

总时间限制: 

10000ms

内存限制: 

65536kB

描述

在国际象棋棋盘上放置八个皇后，要求每两个皇后之间不能直接吃掉对方。

输入

无输入。

输出

按给定顺序和格式输出所有八皇后问题的解（见Sample Output）。

样例输入

样例输出

No. 1
1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0
No. 2
1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0
0 0 0 0 1 0 0 0
0 0 1 0 0 0 0 0
No. 3
1 0 0 0 0 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 1
0 0 1 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0
0 1 0 0 0 0 0 0
0 0 0 0 1 0 0 0
No. 4
1 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1
0 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0
0 0 0 0 0 0 1 0
0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0
No. 5
0 0 0 0 0 1 0 0
1 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0
0 1 0 0 0 0 0 0
0 0 0 0 0 0 0 1
0 0 1 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0
No. 6
0 0 0 1 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 1 0 0 0 0 0
0 0 0 0 0 1 0 0
No. 7
0 0 0 0 1 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1
0 0 0 1 0 0 0 0
0 1 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 1 0 0 0 0 0
0 0 0 0 0 1 0 0
No. 8
0 0 1 0 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0
No. 9
0 0 0 0 1 0 0 0
1 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 1 0 0 0 0 0
...以下省略

提示

此题可使用函数递归调用的方法求解。

来源

计算概论05

三、分析

DFS经典题目

四、AC代码

 //1700:八皇后问题
 /*
 1、首先分析输出样例的顺序
   选第一行，选第二行
   按行的顺序
   说明是指定了列，让我们来填行
 */
 #include <iostream>
 using namespace std;
 //用来存储方案 ,下标都是从1开始
 int a[][];
 int visRow[]; //行
 int visLeftIncline[];//左斜线 使用的时候 row+column
 int visRightIncline[]; //右斜线，使用的时候row-column+8
 int ansCount=;

 void init(){

 }

 void print(){
     cout<<"No. "<<(++ansCount)<<endl;
     for(int i=;i<=;i++){
         for(int j=;j<=;j++){
             cout<<a[i][j]<<" ";
         }
         cout<<endl;
     }

 } 

 void search(int column){
     if(column>){
         //if(ansCount>=5) return;
         print();
         //cout<< ansCount<<endl;
     }
     else{
         for(int row=;row<=;row++){
             if(!visRow[row]&&!visLeftIncline[row+column]&&!visRightIncline[row-column+]){
                 visRow[row]=;
                 visLeftIncline[row+column]=;
                 visRightIncline[row-column+]=;
                 a[row][column]=;
                 search(column+);//找下一列
                 //回溯
                 visRow[row]=;
                 visLeftIncline[row+column]=;
                 visRightIncline[row-column+]=;
                 a[row][column]=;
             }
         }
     }
 }

 int main(){
     init();
     search();
     return ;
 } 

五、注意点

1、注意回溯里面的return

return语句总是返回到调用这个函数的父函数

而在回溯中

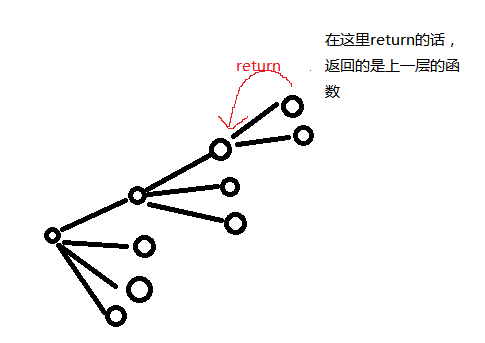
所以在最后面层的return是绝对不会影响到其他函数的计算结果和输出结果的

在以后每次输出结果的时候做一个判断，就能控制结果的输出了