https://www.luogu.org/blog/a23333/post-xing-xuan-mu-ni-sai-path-ji-wang-zui-duan-lu

如果设f[i]表示从i到n的期望

那么转移方程比较好列。

但是取min的环形转移？

反过来想，

如果我们知道了f[x]的大小关系，

其实，可以化简成

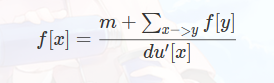
其实就是，我们把一些min变成f[x]然后再消一消。

其实转移貌似没有环了？

但是我们不知道大小关系。

一些边没有用，度数减少一些。

只有比f[x]小的f[y]会转移到x，感觉和最短路有关？

实际上，

把f[n]=0放进堆里，跑一个堆优化dij，每次取出最小点更新相邻的点的f值。

用分析法或者加权平均数可以证明:f[x]<f'[y]<f[y]

所以，这个转移是有意义的，并且转移完成之后，f[y]不可能比f[x]小使得转移变得不合法

而且，可以证明，一个f值被取出的第一次，就是最终的f值。因为能转移到的一定都更新了，不会越更新越小导致能再转移过来。

然后开心dij一下即可。

不放心的话，可以观察最后的实际转移情况，所有转移一定是从比f[x]小的地方转移而来。

12.25模拟赛T2的更多相关文章

  1. 12.25模拟赛T1

    可以区间dp,但是复杂度太高. 所以应该是贪心,怎么贪心呢? 这种题目,最好还是手玩找一些规律. 可以发现,由于保证可以m次填完,所以颜色之间没有相互包含关系. 比较像分治的模型. 所以考虑拿到一个区 ...

  2. 2018.02.12 noip模拟赛T2

    二兵的赌注 Description游戏中,二兵要进入了一家奇怪的赌场.赌场中有n个庄家,每个庄家都可以猜大猜小,猜一次一元钱.每一次开彩前,你都可以到任意个庄家那里下赌注.如果开彩结果是大,你就可以得 ...

  3. 12.25模拟赛T3

    可以发现,答案O(根号)(因为链上答案最大,n/2,n/3...根号种) 每次求答案要二分 优秀的做法是: 对于小于根号n的暴力nlogn找,可能二分到同一个mid,记忆化一下最小的tot值 对于大于 ...

  4. 【2019.8.12 慈溪模拟赛 T2】汪哥图（wang）（前缀和）

    森林 考虑到题目中给出条件两点间至多只有一条路径. 就可以发现,这是一个森林. 而森林有一个很有用的性质. 考虑对于一棵树,点数-边数=\(1\). 因此对于一个森林,点数-边数=连通块个数. 所以, ...

  5. 模拟赛T2 交换 解题报告

    模拟赛T2 交换 解题报告 题目大意: 给定一个序列和若干个区间,每次从区间中选择两个数修改使字典序最小. \(n,m\) 同阶 \(10^6\) 2.1 算法 1 按照题意模拟,枚举交换位置并比较. ...

  6. 5.12 省选模拟赛 T2 贪心 dp 搜索 差分

    LINK:T2 这题感觉很套路 但是不会写. 区间操作 显然直接使用dp不太行 直接爆搜也不太行复杂度太高. 容易想到差分 由于使得整个序列都为0 那么第一个数也要i差分前一个数 强行加一个0 然后 ...

  7. 20180530模拟赛T2——绀碧之棺

    题目背景 qiancl 得到了一张藏宝图,上面写了一道谜题. 题目描述 定义\(F(n)\)为 n 在十进制下各个数位的平方和,求区间\([a,b]\)中有多少\(n\)满足\(k\times F(n ...

  8. light题目讲解 7.25模拟赛T1

    心得:这一道题其实就是自己打暴力打出来的 没有想到正解真的就是暴力枚举 我的做法是这样的 就是枚举A字符串中长度为x的子串 看它是不是B串的子序列 接下来是我的绝望考试代码(100分AC) //lig ...

  9. 20161003 NOIP 模拟赛 T2 解题报告

    Weed duyege的电脑上面已经长草了,经过辨认上面有金坷垃的痕迹. 为了查出真相,duyege 准备修好电脑之后再进行一次金坷垃的模拟实验. 电脑上面有若干层金坷垃,每次只能在上面撒上一层高度为 ...

随机推荐

  1. js 节点

    var chils= s.childNodes; //得到s的全部子节点 var par=s.parentNode;  //得到s的父节点 var ns=s.nextSbiling;  //获得s的下 ...

  2. 一个 mr 作业跑的比较慢，如何来优化。

    mr跑的慢可能有很多原因,如:数据倾斜.map和reduce数设置不合理.reduce等待过久.小文件过多.spill 次数过多. merge 次数过多等. 1.解决数据倾斜:数据倾斜可能是parti ...

  3. linux的date常用命令

    1.显示现在时间 date 2.显示今天日期 date +"%F" date +"%Y-%m-%d" 3.现在时间转化为时间戳 date +%s 4.指定某日期 ...

  4. 2.3 进程控制之exec函数族

    学习目标:学习使用exec函数族的重要的几个函数  一.引言 进程通过exec函数根据指定的文件名或目录名执行另一个可执行文件,当进程调用exec函数时,该进程的数据段.代码段和堆栈段完全被新程序替换 ...

  5. requests模块基础

    requests模块 .caret, .dropup > .btn > .caret { border-top-color: #000 !important; } .label { bor ...

  6. Git 查看远程分支、本地分支、删除本地分支及远程分支

    1. 删除本地分支: git branch -d branchName 2. 删除远程分支: // 方法一:将删除的本地分支推到远程(要删除的远程分支在本地有映射) git push origin : ...

  7. Android ANR 分析

    首先贴一下trace 文件 Process: com.oppo.reader PID: 20358 Time: 2933175644_1545041895232 Flags: 0x38d83e44 P ...

  8. 美年健康股票成交量和K线关系

    看下美年健康的股票,这次主要是研究下成交量和K线的关系,以最后5天为例子,股票下跌成交量降低,说明抛压很小,在最后3天,价格突破的时候,成交量是平时的两倍,说明有机构买入, 业绩部分还可以,全民健身是 ...

  9. 单链表无head各种操作及操作实验

    #encoding=utf-8 class ListNode: def __init__(self,x): self.val=x; self.next=None;   #链表逆序 def revers ...

  10. 11-Mysql数据库----单表查询

    本节重点: 单表查询 语法: 一.单表查询的语法 SELECT 字段1,字段2... FROM 表名 WHERE 条件 GROUP BY field HAVING 筛选 ORDER BY field ...