LibreOJ 6278 数列分块入门 2(分块)

题解:非常高妙的分块,每个块对应一个桶,桶内元素全部sort过,加值时,对于零散块O(sqrt(n))暴力修改,然后暴力重构桶.对于大块直接整块加.查询时对于非完整块O(sqrt(n))暴力遍历.对于完整的大块用lower_bound或者手写二分log(sqrt(n)查找,总复杂度O(n*sqrt(n)*log(sqrt(n)))
代码如下:
#include<cmath>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std; int a[],lump[],tag[];
int n,sz;
vector<int> v[]; void reset(int x)
{
v[x].clear();
for(int i=(x-)*sz+;i<=min(x*sz,n);i++)
{
v[x].push_back(a[i]);
}
sort(v[x].begin(),v[x].end());
} void add(int l,int r,int c)
{
for(int i=l;i<=min(lump[l]*sz,r);i++)
{
a[i]+=c;
}
reset(lump[l]);
if(lump[l]!=lump[r])
{
for(int i=(lump[r]-)*sz+;i<=r;i++)
{
a[i]+=c;
}
reset(lump[r]);
}
for(int i=lump[l]+;i<=lump[r]-;i++)
{
tag[i]+=c;
}
} int query(int l,int r,int c)
{
int ans=;
for(int i=l;i<=min(lump[l]*sz,r);i++)
{
if(a[i]+tag[lump[l]]<c)
{
ans++;
}
}
if(lump[l]!=lump[r])
{
for(int i=(lump[r]-)*sz+;i<=r;i++)
{
if(a[i]+tag[lump[r]]<c)
{
ans++;
}
}
}
for(int i=lump[l]+;i<=lump[r]-;i++)
{
int z=c-tag[i];
ans+=lower_bound(v[i].begin(),v[i].end(),z)-v[i].begin();
}
return ans;
} int main()
{
int opt,l,r,c;
scanf("%d",&n);
sz=sqrt(n);
for(int i=;i<=n;i++)
{
scanf("%d",&a[i]);
}
for(int i=;i<=n;i++)
{
lump[i]=(i-)/sz+;
v[lump[i]].push_back(a[i]);
}
for(int i=;i<=lump[n];i++)
{
sort(v[i].begin(),v[i].end());
}
for(int i=;i<=n;i++)
{
scanf("%d%d%d%d",&opt,&l,&r,&c);
if(!opt)
{
add(l,r,c);
}
else
{
printf("%d\n",query(l,r,c*c));
}
}
}
LibreOJ 6278 数列分块入门 2(分块)的更多相关文章
- LibreOJ 6278. 数列分块入门 2 题解
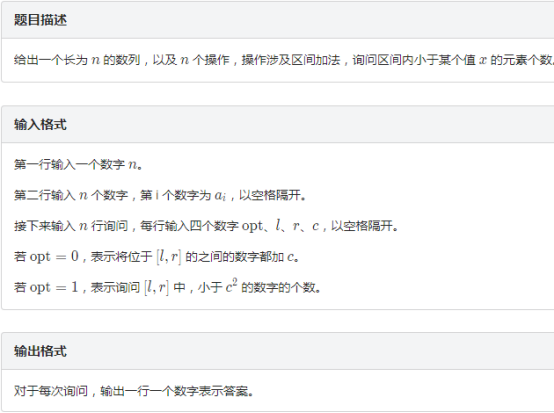
题目链接:https://loj.ac/problem/6278 题目描述 给出一个长为 \(n\) 的数列,以及 \(n\) 个操作,操作涉及区间加法,询问区间内小于某个值 \(x\) 的元素个数. ...
- LibreOJ 6277 数列分块入门 1(分块)
题解:感谢hzwer学长和loj让本蒟蒻能够找到如此合适的入门题做. 这是一道非常标准的分块模板题,本来用打标记的线段树不知道要写多少行,但是分块只有这么几行,极其高妙. 代码如下: #include ...
- LibreOJ 6280 数列分块入门 4(分块区间加区间求和)
题解:分块的区间求和比起线段树来说实在是太好写了(当然,复杂度也高)但这也是没办法的事情嘛.总之50000的数据跑了75ms左右还是挺优越的. 比起单点询问来说,区间询问和也没有复杂多少,多开一个su ...
- LibreOJ 6281 数列分块入门 5(分块区间开方区间求和)
题解:区间开方emmm,这马上让我想起了当时写线段树的时候,很显然,对于一个在2^31次方以内的数,开方7-8次就差不多变成一了,所以我们对于每次开方,如果块中的所有数都为一了,那么开方也没有必要了. ...
- LibreOJ 6279 数列分块入门 3(分块+排序)
题解:自然是先分一波块,把同一个块中的所有数字压到一个vector中,将每一个vector进行排序.然后对于每一次区间加,不完整的块加好后暴力重构,完整的块直接修改标记.查询时不完整的块暴力找最接近x ...
- [Libre 6281] 数列分块入门 5 (分块)
水一道入门分块qwq 题面:传送门 开方基本暴力.. 如果某一个区间全部都开成1或0就打上标记全部跳过就行了 因为一个数开上个四五六次就是1了所以复杂度能过233~ code: //By Menteu ...
- LOJ.6284.数列分块入门8(分块)
题目链接 \(Description\) 给出一个长为n的数列,以及n个操作,操作涉及区间询问等于一个数c的元素,并将这个区间的所有元素改为c. \(Solution\) 模拟一些数据可以发现,询问后 ...
- LOJ.6281.数列分块入门5(分块 区间开方)
题目链接 int内的数(也不非得是int)最多开方4.5次就变成1了,所以还不是1就暴力,是1就直接跳过. #include <cmath> #include <cstdio> ...
- [Libre 6282] 数列分块入门 6 (分块)
原题:传送门 code: //By Menteur_Hxy #include<cstdio> #include<iostream> #include<algorithm& ...
随机推荐
- android栈和队列
android栈和队列 栈和队列是两种特殊的线性表,它们的逻辑结构和线性表相同,只是其运算规则较线性表有更多的限制,故又称它们为运算受限的线性表.LinkedList数据结构是一种双向的链式结构,每一 ...
- ASP.NET WebApi通过自定义ControllerSelector来自定义Controller的选择
在web api中,我们可以通过给Cotroller类添加RoutePrefixAttribute来定义url与Controller之间的映射,但是有时候有一些特殊情况下,我们需要做一些特殊处理来将某 ...
- oscache源码浅析
oscache作为本地缓存框架,存储模型依然是通用的缓存键值对模型.oscache使用HashTable存放数据,我们看下源码: GeneralCacheAdministrator: /** * Ge ...
- 解决Maven提示:Could not read settings.xml, assuming default values
本文转载自:http://blog.csdn.net/hqocshheqing/article/details/47702049 最近在学习Maven 时总是出现 Could not read se ...
- 【转】JMeter脚本的参数化
JMeter脚本的参数化 当你利用Badboy将你的测试脚本录制完毕后,接下来就是脚本的调试工作了.在我看来,调试应该包括有以下几个方面:1.根据测试场景对脚本进行必要的修改:2.脚本参数化:3.添加 ...
- POJ_3740 Easy Finding ——精确覆盖问题,DLX模版
Easy Finding Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 18790 Accepted: 5184 Des ...
- 解决sever 2008中tomcat的报错 init Failed to initialize end point associated with ProtocolHandler ["http-nio-80"]
错误现象: 01-Aug-2017 14:59:50.140 信息 [main] org.apache.coyote.AbstractProtocol.init Initializing Protoc ...
- babel-polyfill使用简介
babel-polyfill介绍 简介 使用这个插件你可随心所欲的使用es6甚至更高版本的方法,这个插件自动转码 安装 这个插件必须在你的源码运行之前运行,所以必须安装成dependency npm ...
- 解读show slave status 命令判断MySQL复制同步状态
解读show slave status 命令判断MySQL复制同步状态 1. show slave status命令可以显示主从同步的状态 MySQL> show slave status \G ...
- vue简单路由(一)
在项目中,将vue的单页面应用程序改为了多页面应用程序,因此在某些场景下,需要频繁的切换两个页面,因此考虑使用路由,这样会减少服务器请求. 使用vue-cli(vue脚手架)快速搭建一个项目的模板(w ...
