【模板】【学习笔记】noip数学

一、素数

欧拉筛

void prime(){
    check[]=;
    for(int i=;i<=n;i++){
        if(!check[i])prim[++cnt]=i;//这个if语句后面没有大括号！！
        for(int j=;j<=cnt&&prim[j]*i<=n;j++){
            check[i*prim[j]]=true;
            if(i%prim[j]==)break;
        }
    }
}

简单的素数判定

bool check(int x){
    if(x<=)return false;
    for(int i=;i*i<=x;i++)
        if(x%i==)return false;
    return true;
}

洛谷p1218搜索+素数判定

二、欧几里得+扩展欧几里得

欧几里得

int gcd(int x,int y){
    return y==?x:gcd(y,x%y);
}

多组gcd预处理

#include<iostream>
#include<cstdio>
using namespace std;
int n,m,g[][];
int main(){
    scanf("%d",&n);
    for(int i=;i<=n;i++){
        g[i][i]=i;g[i][]=g[][i]=i;
        for(int j=;j<i;j++){
            g[j][i]=g[i][j]=g[j][i%j];
        }
    }
    return ;
} 

扩展欧几里得

求逆元：当一个数与它的模数m互质时，那么它在模m意义下的逆元为

这个数的m-2次方。

void exgcd(int a,int b,int &x,int &y){
    if(b==){
        x=;y=;
        return a;
    }
    int r=exgcd(b,a%b,x,y),t;
    t=x;x=y;y=t-a/b*y;
    return r;
}
gcd=exgcd(a,b,x,y);
if(gcd!=)printf("不存在\n")
while(x<=)x+b/gcd;

洛谷p2054

洛谷p1516

三、欧拉函数

phi（n）为小于等于n且与n互质的数的个数。

int get_phi(int x){
    int sum=x;
    if(x%==){
        while(x%==)x/=;
        sum/=;
    }
    for(int i=;i*i<=x;i+=){
        if(x%i==){
            while(x%i==)x/=i;
            sum=sum/i*(i-);
        }
    }
    if(x>)sum=sum/x*(x-);
    return sum;
}

hzwer的

int phi(int n)
{
    int ans=n;
    for(int i=;pri[i]<=sqrt(n);i++)
        if(n%pri[i]==)
        {
            ans=(ans-ans/pri[i]);
            while(n%pri[i]==)n/=pri[i];
        }
    if(n!=)ans=(ans-ans/n);
    return ans%K;
}

int euler(int n){ //返回euler(n)
     int res=n,a=n;
     for(int i=;i*i<=a;i++){
         if(a%i==){
             res=res/i*(i-);//先进行除法是为了防止中间数据的溢出
             while(a%i==) a/=i;
         }
     }
     if(a>) res=res/a*(a-);
     return res;
}
  

hdu2588

四、卡特兰数

不想写了....博客会陆续写几道题的....

去分类里找吧。谢谢滋瓷(。・・)ノ

五、中国剩余定理

设m1,m2,m3,m4两两互素，则同余方程组
x≡a1(m1)
x≡a2(m2)
x≡a3(m3)
x≡a4(m4)
....
x≡ak(mk)
一定有解，x≡(a1*M1*M1^(-1)+a2*M2*M2^(-1)+....)
其中M=m1*m2*...*mk，Mi=M/mi，Mi^(-1)是Mi在模mi意义下的逆元。
普通的中国剩余定理要求所有mi互素，那么如果不互素呢？
我们采用两两合并的思想，假设要合并如下两个方程
x=a1+m1*x1
x=a2+m2*x2
那么得到
a1+m1x1=a2+m2x2 => m1x1+m2x2=a2-a1
再利用扩展欧几里得算法解出x1的最小正整数解，再带入
x=a1+m1x1，得到x后合并为一个方程的结果过为
y≡x(mod lcm(m1,m2))
这样一直合并下去，最终可以求得同余方程的解。
模板：互素的

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;

int a[],m[];
int p,e,i,d,t=;

void exgcd(int a,int b,int &x,int &y){
    if(b==){
        x=;
        y=;
        return;
    }
    exgcd(b,a%b,x,y);
    int tmp=x;
    x=y;
    y=tmp-(a/b)*y;
}

int CRT(int a[],int m[],int n){
    int M=,ans=;
    for(int i=;i<=n;i++)M*=m[i];
    for(int i=;i<=n;i++){
        int x,y;
        int Mi=M/m[i];
        exgcd(Mi,m[i],x,y);
        ans=(ans+Mi*x*a[i])%M;
    }
    if(ans<)ans+=M;
    return ans;
}

int main(){
    while(cin>>p>>e>>i>>d){
        if(p==-&&e==-&&i==-&&d==-)break;
        a[]=p;a[]=e;a[]=i;
        m[]=;m[]=;m[]=;
        int ans=CRT(a,m,);
        if(ans<=d)ans+=;
        printf("Case %d: the next triple peak occurs in %d days.\n",t++,ans-d);
    }
    return ;
}

不互素的

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define N 5
#define ll long long
using namespace std;
ll n,m[N],a[N],m1,e;
ll read()
{
    ll x=,f=; char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-; ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-''; ch=getchar();}
    return x*f;
}
ll exgcd(ll a,ll b,ll &x,ll &y)
{
    if(b==)
    {
        x=,y=;
        return a;
    }
    ll r=exgcd(b,a%b,x,y),tmp;
    tmp=x,x=y,y=tmp-a/b*y;
    return r;
}
ll crt()
{
    ll a1=a[],a2,m2,d,c;m1=m[];
    for(ll i=;i<=n;++i)
    {
        a2=a[i],m2=m[i];
        c=a2-a1;ll x=,y=;
        d=exgcd(m1,m2,x,y);
        if(c%d) return  -;
        x=x*c/d;
        int mod=m2/d;
        x=(mod+x%mod)%mod;
        a1+=m1*x;m1*=mod;
    }
    return a1;
}
int main()
{
//    freopen("mod.in","r",stdin);
//    freopen("mod.out","w",stdout);
    n=;
    for(int i=;i<=n;i++)
     m[i]=read(),a[i]=read();
    printf("%lld\n",crt());
    return ;
}

六、斐波那契

递推公式：f[i]=f[i-1]+f[i-2]，f[1]=f[2]=1

通项公式：

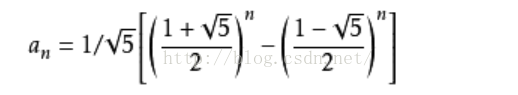
矩阵乘法求斐波那契：

A：(F[i−1]F[i])。B=(01)

(11)

两个矩阵乘一乘就好啦。具体

重要定理：gcd(f[n],f[m])=f[gcd(n,m)]

七、排列组合

排列公式：

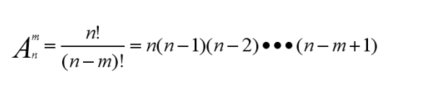
组合数公式：

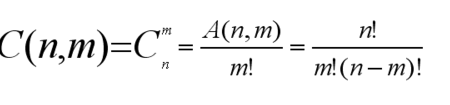
递推法求组合数

    for(int i=;i<=k;i++)
    {
        for(int j=;j<=i;j++)
        {
            if(j==) c[i][j]=;
            else if(i==j) c[i][j]=;
            else c[i][j]=(c[i-][j]%M+c[i-][j-]%M)%M;
        }
    }

如果是计算C(n,m)%p,p是个素数，那么n!/(m!*(n-m)!)=n!*(f[m]*f[n-m])^(p-2)

f[m]为m的阶乘。

Lucas定理：用于大组合数取模问题

插板法:不想多说...来个例题吧...

十、错排

错排：考虑n个元素的一个排列，若每个元素都不在原来的位置，那么这个

排列就叫做原来排列的一个错排。

错排公式：f[i]=(f[i-1]+f[i-2])*(i-1)

错排通项公式：f[n]=n!*[(-1)^2/2!+(-1)^3/3!+(-1)^4/4!+...+(-1)^n/n!]

OpenJudge 9278

十一、容斥原理

容斥原理是一种重要的组合数学的方法，可以让你求解任意组的大小，或者

计算复合事件的概率。

要计算几个集合合并的大小，我们要先将单个集合计算出来，然后减去所有

两个集合相交的部分，再加回所有三个集合相交的部分，再减去所有四个集合

相交的部分。依此类推.....

几个例题：

(1)简单排列问题

0--9组成的排列，要求第一个数字大于1，最后一个数小于8，共有几个排列。

首先算出第一个元素小于等于1（有x种排列）或者最后一个元素大于等于8

（有Y种排列），通过容斥原理写成：

|X|+|Y|-|X∩Y|。经过计算可以写成：

2*9!+2*9!-2*2*8! 就是所有不满足条件的情况，再用总排列10！减去就是答案了。

(2)序列问题

长度为n的由数字0，1，2组成的序列，要求每个数字至少出现1次，这样的序列有

多少种？

定义Ai为不出现数字i的序列数，那么通过容斥原理，我们得到该逆问题的结果为：

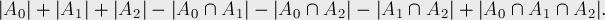
可以发现

每个Ai值都是2^n，而所有两两组合的Ai∩Aj都为1，最后三个集合的交集为0；

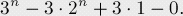
其他没什么好说的，贴上几个题吧。

bzoj1042

bzoj2393