[51nod1482]部落信号 单调栈

~~~题面~~~

题解：

　　可以发现这是一道单调栈的题目，首先来考虑数字没有重复时如何统计贡献。

　　因为这是一个环，而如果我们从最高的点把环断开，并把最高点放在链的最后面（顺时针移动），那么因为在最高点两侧的点无法互相看见，相当于就把环转化为链的问题了。

　　

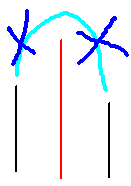
　　因此维护递减的单调栈，如果进来的点比栈顶高就弹出并统计1的贡献。

　　但是这样会有遗漏，我们观察什么情况下会遗漏。

　　因为是从1开始遍历，因此在前面的节点在遍历到n时完全有可能已经被弹走了，然而因为这是一个环，断开点（最高点）说不定还可以回头看见它。因此这种情况会被遗漏。

　　但如果又反着统计又会统计重复，因此考虑不统计最高点的贡献，然后最后再暴力跑2遍统计断开点的贡献。

　　但是数字可能有重复，怎么办？

　　重复数字会带来很多细节上的问题，比如8333中有5的贡献，而直接弹走显然统计不到5.又比如最大值可能有很多个，因此会将整个数列分为很多小段，，，等等诸如此类。

　　因此对于第一种情况，我们记录一下当前栈中每个数字有多少个，因为数字可能很大，但个数不多，因此一开始要离散化一下。

　　对于第二种情况，可以在最后暴力统计一下最高点两两搭配的方案数。
　　细节很多，注意调试&对拍

 #include<bits/stdc++.h>
 using namespace std;
 #define R register int
 #define AC 1001000
 #define LL long long
 
 int n, id, k, maxn, num, last, cnt;
 LL ans;
 int ss[AC], t[AC], tot[AC];
 int s[AC], top;
 bool vis[AC];
 
 inline int read()
 {
     int x = ;char c = getchar();
     while(c > '' || c < '') c = getchar();
     while(c >= '' && c <= '') x = x *  + c - '', c = getchar();
     return x;
 }
 
 inline void upmax(int &a, int b)
 {
     if(b > a) a = b;
 }
 
 inline int get(int x)
 {
     if(x < ) x += n;
     return x > n ? x - n : x;
 }
 
 int half(int x)
 {
     int l = , r = cnt;
     while(l < r)
     {
         int mid = (l + r) >> ;
         if(ss[mid] == x) return mid;
         else if(ss[mid] < x) l = mid + ;
         else r = mid - ;
     }
     return l;
 }
 
 void pre()
 {
     n = read();
     for(R i = ; i <= n; i ++)
     {
         ss[i] = read();
         if(ss[i] > k) id = i, k = ss[i], num = ;
         else if(ss[i] == k) ++ num;
     }
     id = get(id + );
     for(R i = ; i <= n; i ++) t[i] = ss[get(id + i - )];
     sort(ss + , ss + n + );
     for(R i = ; i <= n; i ++)
         if(ss[i] != ss[i + ]) ss[++cnt] = ss[i];
     for(R i = ; i <= n; i ++) t[i] = half(t[i]);
     k = cnt;
 }
 
 /*8
 3 1 5 7 1 1 7 8 */
 void work()
 {
     for(R i = ; i < n; i ++)//不统计中断处的
     {
         int tmp = (top && s[] != t[i]);
     //    printf("%d\n", top);
         while(top && s[top] < t[i]) -- tot[s[top]], -- top, ++ ans;
         if(top && s[top] != t[i]) ++ ans;
         ++ tot[t[i]], s[++top] = t[i];
         if(tot[t[i]] - ) ans += tot[t[i]] -  + tmp;
     //    printf("%d\n", top);
     }
     for(R i = ; i <= n; i ++)
     {
         if(t[i] == k) break;
         if(vis[i]) continue;
         if(t[i] >= maxn && !vis[i]) ++ ans, vis[i] = true;
         upmax(maxn, t[i]);
     }
     maxn = ;
     for(R i = n - ; i; i --)
     {
         if(t[i] == k) break;
         if(t[i] >= maxn && !vis[i]) ++ ans, vis[i] = true;
         upmax(maxn, t[i]);
     }
     if(num > ) ans += num * (num - ) /  - (num - ) * (num - ) / ;
     printf("%lld\n", ans);
 }
 
 int main()
 {
 //    freopen("in.in", "r", stdin);
     pre();
     work();
 //    fclose(stdin);
     return ;
 }