2022-10-03：给定一个正数n，比如6 表示数轴上有 0,1,2,3,4,5,6 ＜0 或者 ＞6 的位置认为无法到达 给定两个数字x和y，0＜= x，y ＜= n 表示小人一开始在x的位置，它

2022-10-03：给定一个正数n，比如6
表示数轴上有 0,1,2,3,4,5,6
<0 或者 >6 的位置认为无法到达
给定两个数字x和y，0<= x，y <= n
表示小人一开始在x的位置，它的目的地是y的位置，比如x = 1, y = 3
给定一个字符串s，比如 : rrlrlr
任何一个s的子序列，对应着一种运动轨迹，r表示向右，l表示向左
比如一开始小人在1位置，"rlr"是s的一个子序列
那么运动轨迹是：1 -> 2 -> 1 -> 2
求，s中有多少个字面值不同的子序列，能让小人从x走到y，
走的过程中完全不走出0到n的区域。
比如，s = “rrlrlr”, n = 6, x = 1, y = 3
有如下5个字面值不同的子序列
rr : 1 -> 2 -> 3
rrlr : 1 -> 2 -> 3 -> 2 -> 3
rrrl : 1 -> 2 -> 3 -> 4 -> 3
rlrr : 1 -> 2 -> 1 -> 2 -> 3
rrlrlr : 1 -> 2 -> 3 -> 2 -> 3 -> 2 -> 3
注意：一定要是字面值不同的子序列！相同字面值的子序列算一种，
比如s中，有很多个rr的子序列，但是算一个，
数据规模 : s串长度 <= 1000, x,y,n <= 2500。
来自SnowFlake。

答案2022-10-03：

动态规划。
如果字符串长度为m，位置数量n。
时间复杂度：O(m * n)。
时间复杂度：O(n)。

代码用rust编写。代码如下：

use std::iter::repeat;
fn main() {
    let ans = ways2("rrlrlr", 6, 1, 3);
    println!("ans = {}", ans);
}

fn ways2(s: &str, n: i32, x: i32, y: i32) -> i32 {
    // all[i] : 让小人来到i位置的不同字面值的子序列数量
    let mut all: Vec<i32> = repeat(0).take((n + 1) as usize).collect();
    // r[i] :   让小人来到i位置的不同字面值，且以r字符结尾，的子序列数量
    let mut r: Vec<i32> = repeat(0).take((n + 1) as usize).collect();
    // l[i] :   让小人来到i位置的不同字面值，且以l字符结尾，的子序列数量
    let mut l: Vec<i32> = repeat(0).take((n + 1) as usize).collect();
    let mut add: Vec<i32> = repeat(0).take((n + 1) as usize).collect();
    // 一开始小人在x，all[x] = 1, {}
    all[x as usize] = 1;
    // M
    for cha in s.bytes() {
        // 当前的指令字符串，cha
        if cha == 'r' as u8 {
            // 当前小人往右走
            // 0 -> 1
            // 1 -> 2
            // 5 -> 6
            // n-1 -> n
            // n -> 死
            // 4  1000
            // 5  +1000
            //
            // 8  200
            // 9 +200
            for i in 0..n {
                // 9 方法数 新增  all[8]
                // 每一个新增方法，都还没有减去修正值呢！
                add[(i + 1) as usize] += all[i as usize];
            }
            for i in 0..=n {
                // 变了！成了纯新增！
                add[i as usize] -= r[i as usize];
                all[i as usize] += add[i as usize];
                r[i as usize] += add[i as usize];
                add[i as usize] = 0;
            }
        } else {
            // 遇到的是l
            // 当前小人往左走
            // 0 左 死
            // 1    0
            // 2    1
            // 3    2
            for i in 1..=n {
                //  7 新增  之前8位置方法数
                add[(i - 1) as usize] += all[i as usize];
            }
            for i in 0..=n {
                // 修正，变成纯新增!
                add[i as usize] -= l[i as usize];
                all[i as usize] += add[i as usize];
                l[i as usize] += add[i as usize];
                add[i as usize] = 0;
            }
        }
    }
    // 去重的！
    return all[y as usize];
}

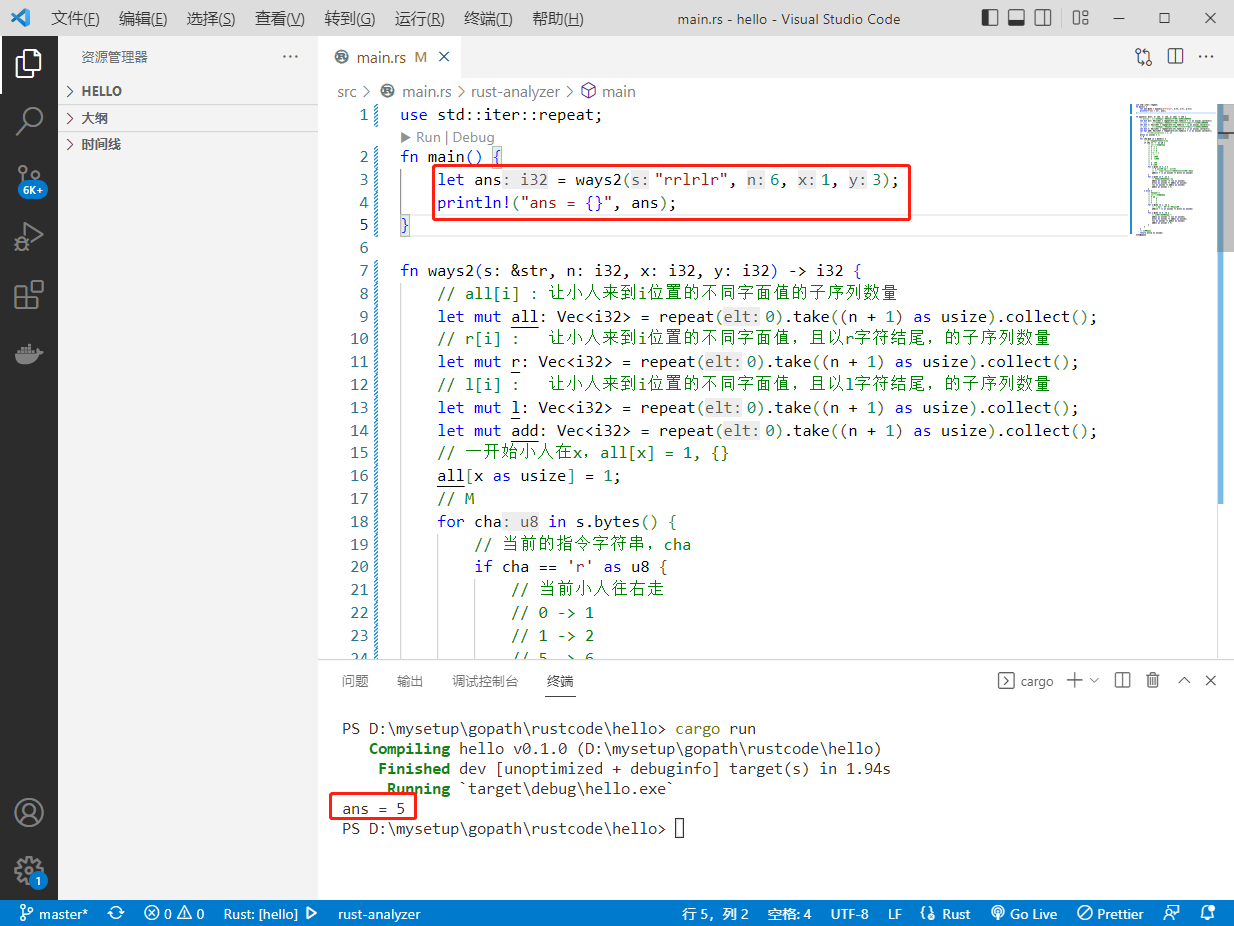
执行结果如下：

---

左神java代码