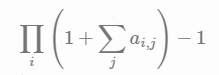[CSP-S 2019 day2 T1] Emiya家今天的饭
题面

题解
不考虑每种食材不超过一半的限制,答案是
减去 1 是去掉一道菜都不做的方案。
显然只可能有一种菜超过一半,于是枚举这种菜,对每个方式做背包即可(记一维状态表示这种菜比别的菜多做了多少份)。
设dp[i][j]为前i种方法中这种食材比别人多j份,
则
于是从零开始枚举j就行了
吗
不对,我们可以意识到dp[i][ - | j |]也对答案有影响,

所以我们设dp[i][n]为原先的dp[i][0],n以下的是负数情况
#include<cstdio>
#include<iostream>
#include<cstring>
#define LL long long
using namespace std;
int read() {
int f = 1,x = 0;char s = getchar();
while(s < '0' || s > '9') {if(s == '-') f = -1;s = getchar();}
while(s >= '0' && s <= '9') {x = x * 10 + s - '0';s = getchar();}
return x * f;
}
int mod = 998244353;
int n,m,i,j,s,o,k;
LL a[105][2005];
LL dp[2][205];
LL ans = 0;
int main() {
// freopen("meal.in","r",stdin);
// freopen("meal.out","w",stdout);
n = read();m = read();
ans = 1;
for(int i = 1;i <= n;i ++) {
for(int j = 1;j <= m;j ++) {
a[i][j] = read();
a[i][0] += a[i][j];
a[i][0] %= mod;
}
ans = ans * (a[i][0] + 1ll) % mod;
}
ans = (ans + mod - 1ll) % mod;
// printf("%lld\n",ans);
for(register int k = 1;k <= m;k ++) {
dp[0][n] = 1;
for(register int i = 1;i <= n;i ++) {
for(register int j = n + i;j >= n - i;j --) {
if(j) dp[i&1][j] = ((dp[1-(i&1)][j + 1] *1ll* (a[i][0] - a[i][k] + mod) % mod) + dp[1-(i&1)][j] + dp[1-(i&1)][j - 1] * a[i][k] % mod) % mod;
else dp[i&1][j] = ((dp[1-(i&1)][j + 1] *1ll* (a[i][0] - a[i][k] + mod) % mod) + dp[1-(i&1)][j]) % mod;
}
}
for(register int j = n + 1;j <= 2*n;j ++) {
ans = (ans + mod - dp[n&1][j]) % mod;
dp[0][j] = 0;
dp[0][j - n] = 0;
dp[1][j] = 0;
dp[1][j - n] = 0;
// printf("%lld ",dp[n&1][j]);
}//putchar('\n');
}
printf("%lld\n",ans);
return 0;
}[CSP-S 2019 day2 T1] Emiya家今天的饭的更多相关文章
- 【CSP-S 2019】D2T1 Emiya 家今天的饭
Description 传送门 Solution 算法1 32pts 爆搜,复杂度\(O((m+1)^n)\) 算法2 84pts 裸的dp,复杂度\(O(n^3m)\) 首先有一个显然的性质要知道: ...
- 洛谷P5664 Emiya 家今天的饭 问题分析
首先来看一道我编的题: 安娜写宋词 题目背景 洛谷P5664 Emiya 家今天的饭[民间数据] 的简化版本. 题目描述 安娜准备去参加宋词大赛,她一共掌握 \(n\) 个 词牌名 ,并且她的宋词总共 ...
- 洛谷P5664 Emiya 家今天的饭 题解 动态规划
首先来看一道题题: 安娜写宋词 题目背景 洛谷P5664 Emiya 家今天的饭[民间数据] 的简化版本. 题目描述 安娜准备去参加宋词大赛,她一共掌握 \(n\) 个 词牌名 ,并且她的宋词总共有 ...
- [CSP-S 2019 Day2]Emiya家今天的饭
思路: 这种题目就考我们首先想到一个性质.这题其实容易想到:超限的菜最多只有一个,再加上这题有容斥那味,就枚举超限的菜然后dp就做完了. 推式子能力还是不行,要看题解. 式子还需要一个优化,就是废除冗 ...
- 【CSP-S 2019】【洛谷P5664】Emiya 家今天的饭【dp】
题目 题目链接:https://www.luogu.org/problem/P5664 Emiya 是个擅长做菜的高中生,他共掌握 \(n\) 种烹饪方法,且会使用 \(m\) 种主要食材做菜.为了方 ...
- Emiya家今天的饭 NOIP2019 (CSP?) 类DP好题 luoguP5664
luogu题目传送门! 首先,硬求可行方案数并不现实,因为不好求(去年考场就这么挂的,虽然那时候比现在更蒟). 在硬搞可行方案数不行之后,对题目要求的目标进行转换: 可行方案数 = 总方案数 - 不合 ...
- 「CSP-S 2019」Emiya 家今天的饭
description loj 3211 solution 看到题目中要求每种主要食材至多在一半的菜中被使用,容易想到补集转换. 即\(ans=\)总方案数-存在某一种食材在一半以上的菜中被使用的方案 ...
- CSP-S 2019 Emiya 家今天的饭
64 pts 类似 乌龟棋 的思想,由于 \(64pts\) 的 \(m <= 3\), 非常小. 我们可以设一个 \(dp\),建立 \(m\) 个维度存下每种物品选了几次: \(f[i][A ...
- [CSP-S2019]Emiya 家今天的饭 题解
CSP-S2 2019 D2T1 很不错的一题DP,通过这道题学到了很多. 身为一个对DP一窍不通的蒟蒻,在考场上还挣扎了1h来推式子,居然还有几次几乎推出正解,然而最后还是只能打个32分的暴搜滚粗 ...
随机推荐
- 树莓派开发笔记(十七):树莓派4B+上Qt多用户连接操作Mysql数据库同步(单条数据悲观锁)
前言 安装了mysq数据库,最终时为了实现在一个树莓派上实现多用户多进程操作的同步问题,避免数据并发出现一些错误,本篇安装了远程服务并且讲述了使用Qt进行悲观锁for update操作,命令行进行 ...
- 【Java面试】介绍下Spring IoC的工作流程
Hi,我是Mic 一个工作了4年的粉丝,在面试的时候遇到一个这样的问题. "介绍一下Spring IOC的工作流程" 他说回答得不是很好,希望我能帮他梳理一下. 关于这个问题,我们 ...
- 几种常见的DoS攻击
DoS为Denial of Service的简称,意思是拒绝服务.DoS攻击是一种使被攻击者无法正常提供服务的攻击.常见的攻击方式有以下几种类型: LAND Local Area Network ...
- 训练一个图像分类器demo in PyTorch【学习笔记】
[学习源]Tutorials > Deep Learning with PyTorch: A 60 Minute Blitz > Training a Classifier 本文相当于 ...
- 拉取服务器上的项目,svn认证失败
解决方案: 在服务器上找到对应的项目路径,并修改authz: 我的是因为[group]组下(下图中34行),我写的是[demo:/],改为[/]就可以了.
- ByDesign各版本区别
by zyi
- 数组基础篇(对应C++ Primer plus 4.10)
概要:数组是由一组同类型的元素组成的集合,在内存上是一片连续的存储空间.C++提供了三种数组的表示方法:普通数组,模板类vector(C++98 新增的标准模板库STL提供该模板类)和模板类array ...
- Unity3D学习笔记8——GPU实例化(3)
目录 1. 概述 2. 详论 2.1. 自动实例化 2.2. MaterialPropertyBlock 3. 参考 1. 概述 在前两篇文章<Unity3D学习笔记6--GPU实例化(1)&g ...
- “杀死” App 上的疑难崩溃
在移动应用性能方面,崩溃带来的影响是最为严重的,程序崩了可以打断用户正在进行的操作体验,造成关键业务中断.用户留存率下降.品牌口碑变差.生命周期价值下降等影响.很多公司将崩溃率作为优先级最高的技术指标 ...
- maven项目(引入依赖失败, pom.xml 报错\爆红)
引入项目过程中,idea引入磁盘的某个的maven项目 这里以springboot项目以例子,发现pom.xml 的依赖大面积爆红,springboot的版本依赖也报错了,然后发现下面有进度条在下载, ...