深度优先搜索算法-dfs讲解

迷宫问题

有一个迷宫：

S**.
....
***T

（其中字符S表示起点，字符T表示终点，字符*表示墙壁，字符.表示平地。你需要从S出发走到T，每次只能向上下左右相邻的位置移动，不能走出地图，也不能穿过墙壁，每个点只能通过一次。）

现在需要你求出是否可以走出这个迷宫

我们将这个走迷宫过程称为dfs（深度优先搜索）算法。

思路

当我们搜索到了某一个点，有这样3种情况：

1.当前我们所在的格子就是终点。

2.如果不是终点，我们枚举向上、向下、向左、向右四个方向，依次去判断它旁边的四个点是否可以作为下一步合法的目标点，如果可以，那么我们就进行这一步，走到目标点，然后继续进行操作。

3.当然也有可能我们走到了“死胡同”里（上方、下方、左方、右方四个点都不是合法的目标点），那么我们就回退一步，然后从上一步所在的那个格子向其他未尝试的方向继续枚举。

怎样才能算“合法的目标点”？

1.必须在所给定的迷宫范围内

2.不能是迷宫边界或墙。

3.这个点在搜索过程中没有被走过（这样做是因为，如果一个点被允许多次访问，那么肯定会出现死循环的情况——在两个点之间来回走。）

实现代码

#include <iostream>
using namespace std;
int n, m;
string maze[105];
int sx, sy;
bool vis[105][105];
int dir[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};//四个方向的方向数组
bool in(int x, int y) {
    return 0 <= x && x < n && 0 <= y && y < m;
}
bool dfs(int x, int y) {
    vis[x][y] = 1;//点已走过标记
    if (maze[x][y] == 'T') {//到达终点
        return 1;
    }
    for (int i = 0; i < 4; ++i) {
        int tx = x + dir[i][0];
        int ty = y + dir[i][1];
        if (in(tx, ty) && !vis[tx][ty] && maze[tx][ty] != '*') {
            /*
            1.in(tx, ty) : 即将要访问的点在迷宫内
            2.!vis[tx][ty] : 点没有走过
            3.maze[tx][ty] != '*' : 不是墙
            */
            if (dfs(tx, ty)) {
                return 1;
            }
        }
    }
    return 0;
}
int main() {
    cin >> n >> m;
    for (int i = 0; i < n; ++i) {
        cin >> maze[i];
    }
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < m; ++j) {
            if (maze[i][j] == 'S') {
                //记录起点的坐标
                sx = i;
                sy = j;
            }
        }
    }
    if (dfs(sx, sy)) {
        puts("Yes");
    } else {
        puts("No");
    }
    return 0;
}

深搜的剪枝优化

可行性剪枝

剪枝，顾名思义，就是通过一些判断，砍掉搜索树上不必要的子树。有时候，在搜索过程中我们会发现某个结点对应的子树的状态都不是我们要的结果，那么我们其实没必要对这个分支进行搜索，直接“砍掉”这棵子树（直接 return退出），就是"剪枝"。

我们举一个例子：

给定n个整数，要求选出K个数，使得选出来的K个数的和为sum。

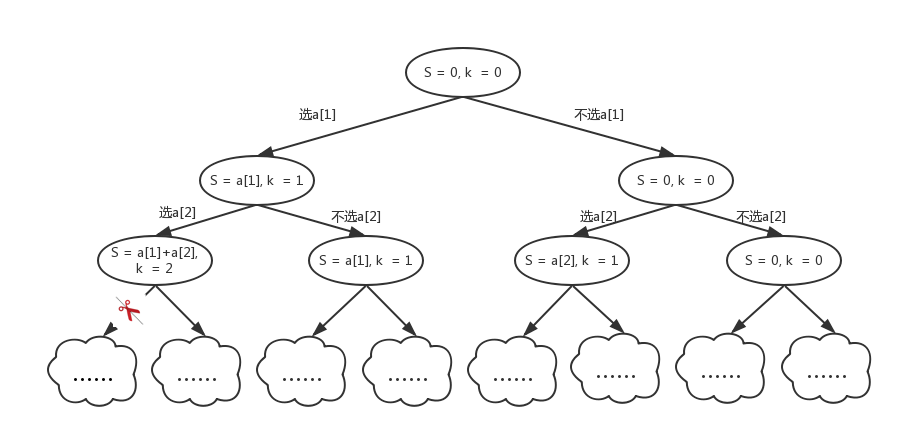
如上图，当k=2的时候，如果已经选了2个数，再往后选更多的数是没有意义的。所以我们可以直接减去这个搜索分支，对应上图中的剪刀减去的那棵子树。

又比如，如果所有的数都是正数，如果一旦发现当前和的值都已经大于sum了，那么之后不管怎么选，选择数的和都不可能是sum了，就可以直接终止这个分支的搜索。

例：从1,2,3,⋯,30这30个数中选8个数，使得和为200。

我们可以加如下剪枝

if (数字个数 > 8) return ;

if (总和 > 200) return ;

经过尝逝后发现：

没有剪枝

加剪枝：

最优性剪枝

我们再看一个问题：

有一个n×m大小的迷宫。其中字符S表示起点，字符T表示终点，字符*表示墙壁，字符.表示平地。你需要从S出发走到T，每次只能向上下左右相邻的位置移动，并且不能走出地图，也不能走进墙壁。保证迷宫至少存在一种可行的路径，输出S走到T的最少步数。

对于求最优解（从起点到终点的最小步数）这种问题，通常可以用最优性剪枝，比如在求解迷宫最短路的时候，如果发现当前的步数已经超过了当前最优解，那从当前状态开始的搜索都是多余的，因为这样搜索下去永远都搜不到更优的解。通过这样的剪枝，可以省去大量冗余的计算。

此外，在搜索是否有可行解的过程中，一旦找到了一组可行解，后面所有的搜索都不必再进行了，这算是最优性剪枝的一个特例。

现在我们考虑用dfs来解决这个问题，第一个搜到的答案res并不一定是正解，但是正解一定小于等于res。于是如果当前步数大于等于res就直接剪枝。

在dfs函数内加入如下代码

if (目前步数 >= res) return ;

if (目前所处的位置字符 == 'T') {
    答案 = 目前步数;//因为我们在刚才已经进行了一次剪枝，所以我们现在是可以保证目前答案大于之前答案的
    return ;
}

好啦，到这里就结束了捏~

求赞qwq