Note -「模拟退火」

随机化算法属于省选芝士体系

0x01 前置芝士

你只需要会 rand 就可以啦！

当然如果你想理解的更透彻也可以先看看爬山算法

0x02 关于退火

退火是一种金属热处理工艺，指的是将金属缓慢加热到一定温度，保持足够时间，然后以适宜速度冷却。目的是降低硬度，改善切削加工性；消除残余应力，稳定尺寸，减少变形与裂纹倾向；细化晶粒，调整组织，消除组织缺陷。准确的说，退火是一种对材料的热处理工艺，包括金属材料、非金属材料。而且新材料的退火目的也与传统金属退火存在异同。

也就是你可以理解为，金属在逐渐降温的过程中，它含的某种物质会趋于恒定。

换成 OI 的话说，如果每个温度对应一个答案，则随着温度越来越小，答案波动的范围就会越来越小，最后答案趋于恒定。例如下面这个经典图片，便是利用这个思想，最后得到了一个多峰函数的最值。模拟退火就是用于求解多峰函数的最值问题。

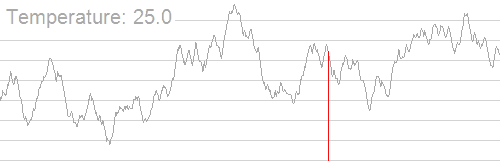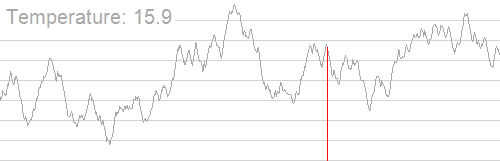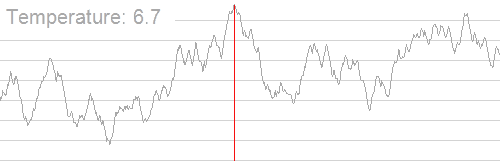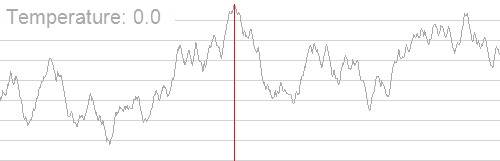
不过是不是看起来很玄学？现在我们来细化一下模拟退火思想。

0x03 模拟退火

你如果仔细看，刚刚那个图中答案好像和温度没有直接联系，也就是说答案是随机的。这个说法不太完全，答案和温度确实没有太大联系，但温度却可以限定答案所在的范围。

首先我们引入几个参数：当前最优解 \(A_0\)，新的解 \(A\)，上一个被接纳的解 \(A_1\)，解的“变动量” \(ΔA\)（即 \(A\) 与 \(A_0\) 的差值，这里规定为 \(A - A_0\)），开始的温度 \(T_0\)，当前温度 \(T\)，最终的温度 \(T_{esp}\)。温度变动量 \(q\)。接纳：指对于一个解，我们认为它有可能是正确答案，或者说与正确答案有联系。

以下均以求多峰函数最大值为例来模拟整个过程。

首先在一开始，我们找到一个你认为接近正确答案的解 \(A_1\)，将 \(A_0\) 初始置为 \(A_1\)。然后你需要在温度限制的范围内，去合理的再取到一个解，即 \(A\)。至于这个温度限制的范围其实很简单，你只需要求到一个满足条件的随机数即可。例如：你有一个横坐标，如果你要再求到一个横坐标，你就可以写成。

double cx = now.x + ((rand() << 1) - RAND_MAX) * t;

// RAND_MAX 是 <stdlib.h> 中的一个宏，也就是随机数的最大值。

// 通过 (rand << 1) - RAND_MAX 我们就得到了一个可能为正可能为负的随机数

这样的话，你就会发现随着 \(T\) 的不断减小，新的解与上一个解的差距就越小，即达到了我们的目的。

现在我们有了 \(A\)，自然就可以求到所谓 \(ΔA\)。

得到 \(ΔA\)后：

\(ΔA > 0\) ：也就是说当前解大于当前最优解，因为我们是求最大值，所以此时显然更新 \(A_0\)，并更新 \(A_1 = A\)。
\(ΔA \leq 0\) ：这就比较麻烦了，首先这样的情况是肯定不能更新 \(A_0\) 的。但我们考虑一下 \(A_1\)，如果接纳 \(A\)，那么我们下次就是从 \(A\) 开始扩展新的点，这很明显有可能不是最优的（你从多峰函数的一个峰的半山腰跌到了一个山谷）。但也有可能是更优的，因为你现在接纳的这个点，它可能不在最终答案的那一座峰上，所以你需要跳往另一座峰，也就是你需要接纳 \(A\)。这下该怎么办呢？有一个非常玄学的东西，叫：Metropolis接受准则。它告诉我们有一定概率去接纳 \(A\)，而这个概率只需比较 \(\exp(-delta / t) * RAND\_MAX\) 和 \(rand()\) 的大小即可。

在做完这些操作后，我们让 \(T = T \times q\)。

好了，我们现在又有了一个 \(A_1\)，这个 \(A_1\) 可能等于 \(A_0\) 也可能等于 \(A\)。我们将这个 \(A_1\) 再去执行上述操作，反复执行，随着温度的减小，我们就可以求到一个趋于恒定的答案了！

当然还有几个未处理的地方。

首先：

\(T_0\) 的取值：根据题目而定，我通常使用 \(2000\) 到 \(5000\) 的一个整数。
\(q\) 的取值：在前人的总结中，\(q\) 近似于 \(0.996\)。
\(T_{esp}\) 的取值：这也需要视题目而定，如果这个值越小，按理说答案精度就越大，所以如果你不怕超时就可以开的小一点。

最后，关于时间复杂度，因为此算法使用了大量随机数，所以其时间复杂度近似于 \(O(rp)\)。

0x04 例题

LINK

一句话题意：给定 \(n\) 个坐标，求这 \(n\) 个坐标的费马点。

定义 \(sum\) 表示一个坐标到 \(n\) 个点的距离和。

首先，你会发现答案是一个函数，因为一个坐标只对应一个 \(sum\)。于是我们其实就是要求这个多峰函数 \(sum\) 的最小值。

那么就是模拟退火嘛。读者可以在根据下面这个代码理解一下实现。

值得注意的是，这道题函数 \(sum\) 的“横坐标”是一个坐标。

#include <bits/stdc++.h>

using namespace std;

int read() {

    int k = 1, x = 0;

    char s = getchar();

    while (s < '0' || s > '9') {

        if (s == '-')

            k = -1;

        s = getchar();

    }

    while (s >= '0' && s <= '9') {

        x = (x << 3) + (x << 1) + s - '0';

        s = getchar();

    }

    return x * k;

}

const int MAXN = 5e3 + 5;

const double q = 0.996;

// 温度变动量

struct node {

    double x, y;

    node() {}

    node(double X, double Y) {

        x = X;

        y = Y;

    }

} a[MAXN], now, anst;

// now 初值为 A1，在这里是 (0, 0)

double ans = 1e18;

// 答案初值

int n;

double f(double x, double y) {

    double ret = 0;

    for (int i = 1; i <= n; i++) ret += sqrt((x - a[i].x) * (x - a[i].x) + (y - a[i].y) * (y - a[i].y));

    return ret;

}

void Make_Fire() {

    double t = 3000;

    while (t > 1e-16) {

        double cx = now.x + ((rand() << 1) - RAND_MAX) * t;

        double cy = now.y + ((rand() << 1) - RAND_MAX) * t;

        // 求到 A 的横坐标，在这里是 (cx, cy)

        double cnt = f(cx, cy);

        // 求到 A

        double delta = cnt - ans;

        // 求到差

        if (delta < 0) { // 如果差是小于 0 的

            now = node(cx, cy);

            // 接纳它

            anst = node(cx, cy);

            // 根据题目需要，更新答案的坐标

            ans = cnt;

            // 跟新答案

        } else if (exp(-delta / t) * RAND_MAX > rand())

        // 玄学接受准则

            now = node(cx, cy);

            // 接纳它

        t *= q;

        // 降温

    }

}

int main() {

    srand(998244353);

    n = read();

    ans = 1e18;

    for (int i = 1; i <= n; i++)

        scanf("%lf %lf", &a[i].x, &a[i].y);

    for (int i = 1; i <= 5; i++) Make_Fire();

    printf("%.2lf %.2lf\n", anst.x, anst.y);

    return 0;

}