launch edge 和 latch edge 延迟

本文转自 http://www.cnblogs.com/inet2012/archive/2012/03/07/2384149.html

launch edge和latch edge分别是指一条路径的起点和终点，只是一个参考时间，本身没有什么意义，latch_edge-launch_edge才有意义。

1. 背景

静态时序分析的前提就是设计者先提出要求，然后时序分析工具才会根据特定的时序模型进行分析，给出正确是时序报告。

　　进行静态时序分析，主要目的就是为了提高系统工作主频以及增加系统的稳定性。对很多数字电路设计来说，提高工作频率非常重要，因为高工作频率意味着高处理能力。通过附加约束可以控制逻辑的综合、映射、布局和布线，以减小逻辑和布线延时，从而提高工作频率。

2. 理论分析

2.1 固定参数launch edge、latch edge、Tsu、Th、Tco概念

2.1.1 launch edge

　　时序分析起点（launch edge）：第一级寄存器数据变化的时钟边沿，也是静态时序分析的起点。

2.1.2 latch edge

　　时序分析终点（latch edge）：数据锁存的时钟边沿，也是静态时序分析的终点。

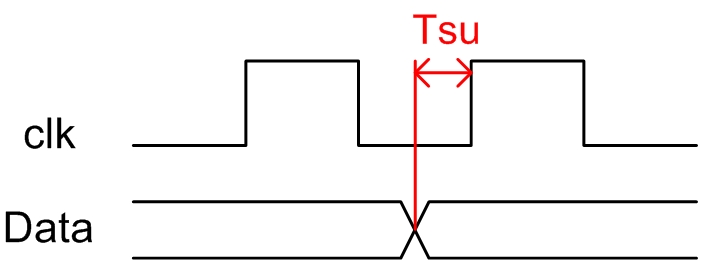
2.1.3 Clock Setup Time (Tsu)

　　建立时间（Tsu）：是指在时钟沿到来之前数据从不稳定到稳定所需的时间，如果建立的时间不满足要求那么数据将不能在这个时钟上升沿被稳定的打入触发器。如图3.2所示：

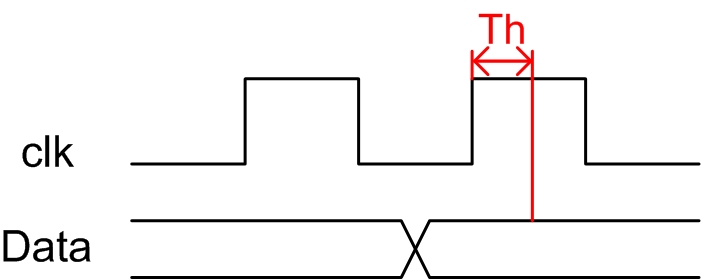
2.1.4 Clock Hold Time (Th)

　　保持时间（Th）：是指数据稳定后保持的时间，如果保持时间不满足要求那么数据同样也不能被稳定的打入触发器。保持时间示意图如图3.3所示：

2.1.5 Clock-to-Output Delay（tco）

　　数据输出延时（Tco）：这个时间指的是当时钟有效沿变化后，数据从输入端到输出端的最小时间间隔。

2.2 Clock skew

　　时钟偏斜（clock skew）：是指一个时钟源到达两个不同寄存器时钟端的时间偏移，如图3.4所示：

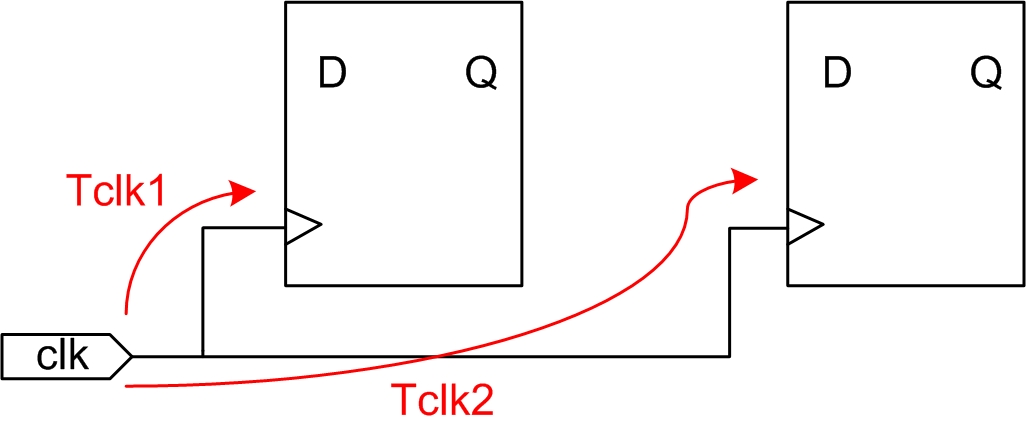
时钟偏斜计算公式如下：

Tskew = Tclk2 - Tclk1　　　　　　　　　　　（公式2-1）

2.2 Data Arrival Time

　　数据到达时间（Data Arrival Time）：输入数据在有效时钟沿后到达所需要的时间。主要分为三部分：时钟到达寄存器时间（Tclk1），寄存器输出延时（Tco）和数据传输延时（Tdata），如图3.5所示

数据到达时间计算公式如下：

　　　Data Arrival Time = Launch edge + Tclk1 +Tco + Tdata　　　　　　　　（公式2-2）

2.3 Clock Arrival Time

　　时钟到达时间（Clock Arrival Time）：时钟从latch边沿到达锁存寄存器时钟输入端所消耗的时间为时钟到达时间，如图3.6所示

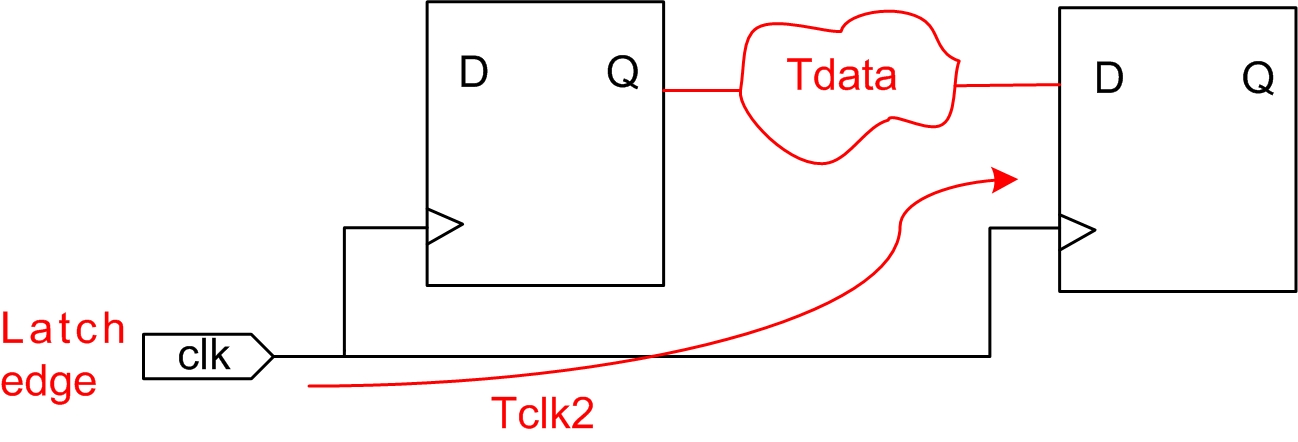
图3.6 时钟到达时间

时钟到达时间计算公式如下：

　Clock Arrival Time = Lacth edge + Tclk2　　　　　　　　　　　　　　（公式2-3）

2.4 Data Required Time（setup/hold）

　　数据需求时间（Data Required Time）：在时钟锁存的建立时间和保持时间之间数据必须稳定，从源时钟起点达到这种稳定状态需要的时间即为数据需求时间。如图3.7所示：

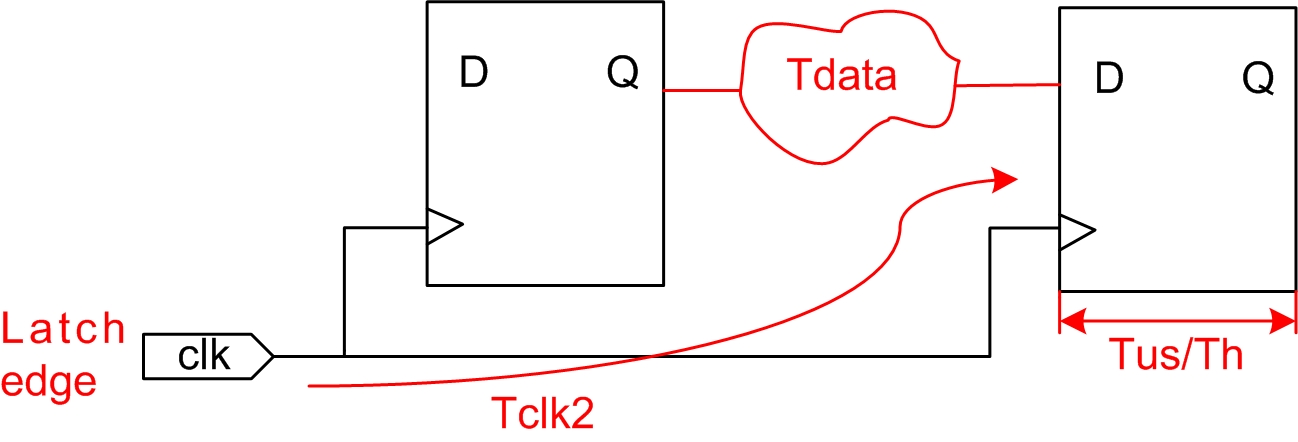
图3.7 数据需求时间

（建立）数据需求时间计算公式如下：

　　　　　　　　　Data Required Time = Clock Arrival Time - Tsu　　　　　　　　　　　　（公式2-4）

（保持）数据需求时间计算公式如下：

Data Required Time = Clock Arrival Time + Th     （公式2-5）　

2.5 Setup slack

　　建立时间余量（setup slack）：当数据需求时间大于数据到达时间时，就说时间有余量，Slack是表示设计是否满足时序的一个称谓。

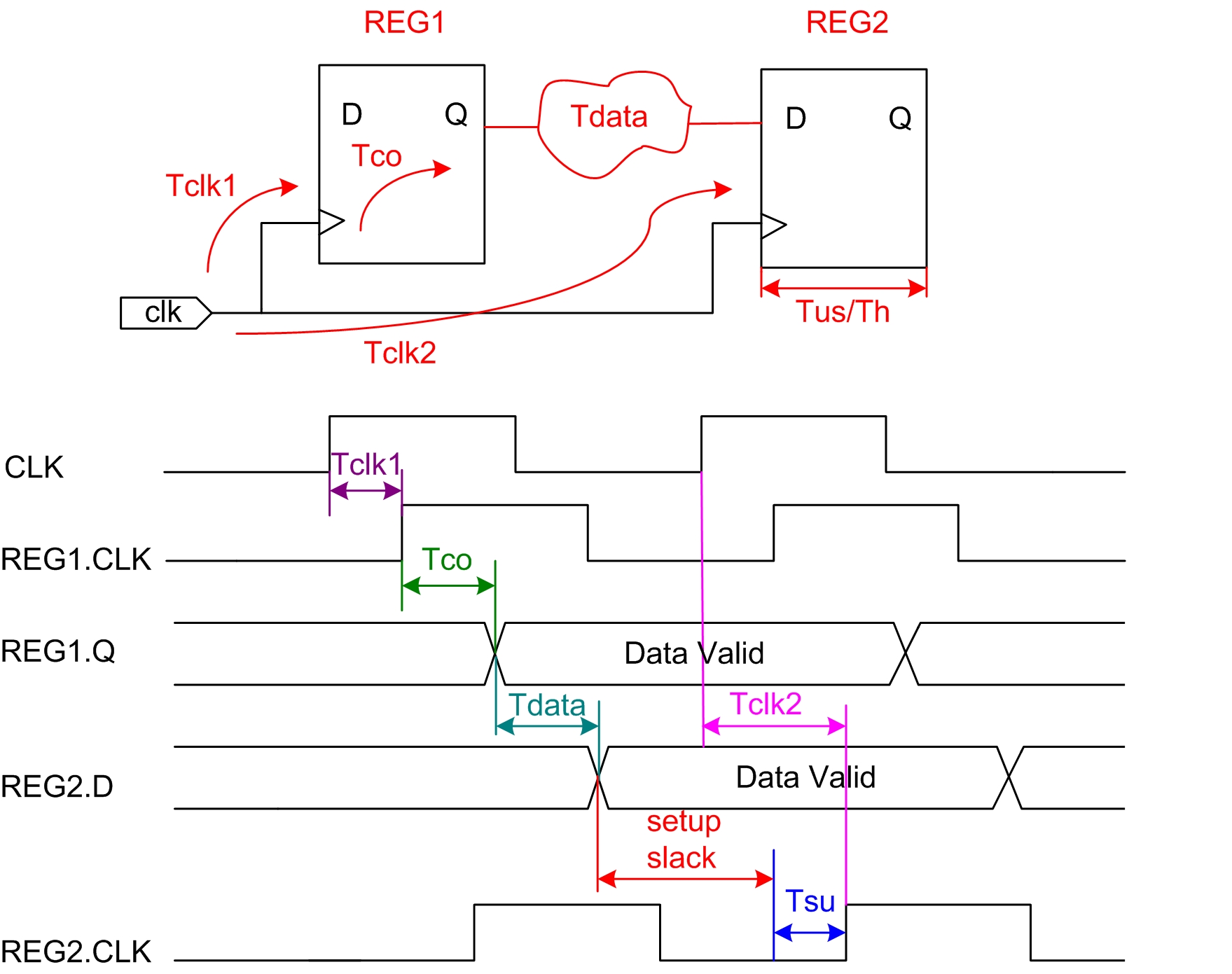
图3.8 建立时间余量

　　如图3.8所示，建立时间余量的计算公式如下：

　　　　　　　　　　Setup slack = Data Required Time - Data Arrival Time　　　　　　　　（公式2-6）

　　由公式可知，正的slack表示数据需求时间大于数据到达时间，满足时序（时序的余量），负的slack表示数据需求时间小于数据到达时间，不满足时序（时序的欠缺量）。

3.1.7 时钟最小周期

　　时钟最小周期：系统时钟能运行的最高频率。

　　1.　 当数据需求时间大于数据到达时间时，时钟具有余量；

　　2. 当数据需求时间小于数据到达时间时，不满足时序要求，寄存器经历亚稳态或者不能正确获得数据；

　　3. 当数据需求时间等于数据到达时间时，这是最小时钟运行频率，刚好满足时序。

　　从以上三点可以得出最小时钟周期为数据到达时间等于数据需求时间，的运算公式如下：

Data Required Time = Data Arrival Time　

---

另附：图解Setup 与 Hold Slack

从上面图中可以清晰的看出Setup与Hold Slack的定义与计算方法:

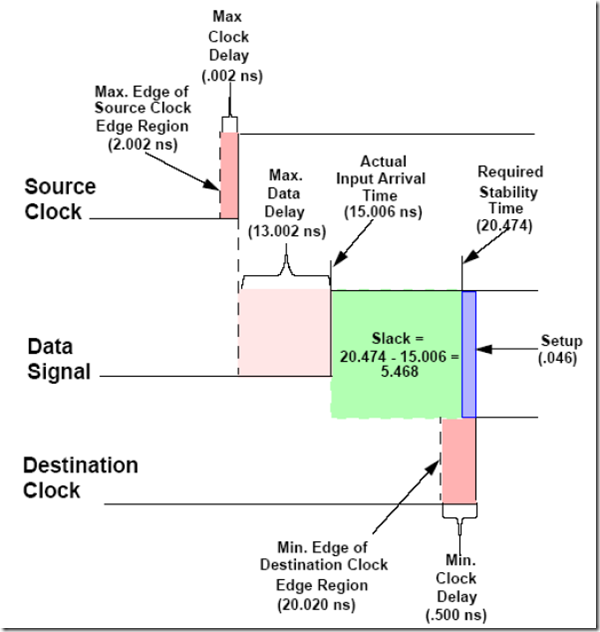
Setup slack=latch edge+Tclk2-Tsu-(launch edge+Tclk1+Tco+Tdata)

=(latch edge-lanuch edge)+(Tclk2-Tclk1)-(Tsu+Tco+Tdata)

对于工具默认的单周期来说，latch edge-lanuch edge=T，如果不考虑时钟的skew，Tclk2-Tclk1=0，上式可以表达成：

Setup slack=T-(Tsu+Tco+Tdata),这就是为什么说源寄存器与目的寄存器之间延迟不能太长的原因，延迟越长，slack越小。

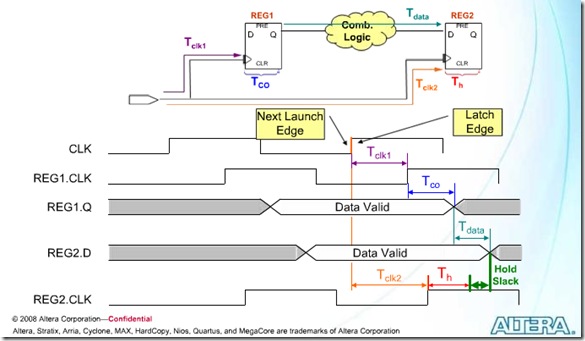
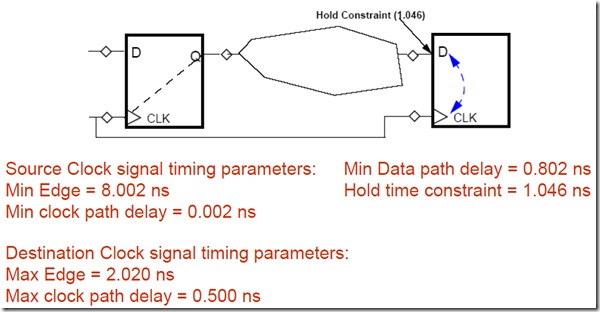
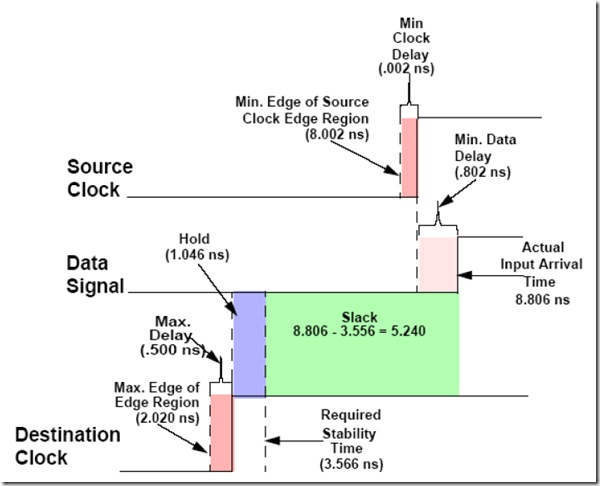
Hold slack=data arrival time – data required time
=(launch edge + Tclk1 + Tco + Tdata) – (latch edge + Tclk2 + Th)
=(launch edge – latch edge) – (Tclk2 – Tclk1) + (Tco + Tdata + Th)

注意，上式中的launch edge为next launch edge，即为latch edge，所以launch edge – latch edge=0，如果不考虑时钟的skew，Tclk2-Tclk1=0，上式可以表达成：

Hold slack=Tco + Tdata – Th，这就是为什么说源寄存器与目的寄存器之间延迟不能太短的原因，时间太短，slack越小。

setup slack 计算

hold slack 计算