二叉堆的实现(数组）——c++

二叉堆的介绍

二叉堆是完全二元树或者是近似完全二元树，按照数据的排列方式可以分为两种：最大堆和最小堆。
最大堆：父结点的键值总是大于或等于任何一个子节点的键值；最小堆：父结点的键值总是小于或等于任何一个子节点的键值。示意图如下：

二叉堆一般都通过"数组"来实现。数组实现的二叉堆，父节点和子节点的位置存在一定的关系。有时候，我们将"二叉堆的第一个元素"放在数组索引0的位置，有时候放在1的位置。当然，它们的本质一样(都是二叉堆)，只是实现上稍微有一丁点区别。
假设"第一个元素"在数组中的索引为 0 的话，则父节点和子节点的位置关系如下：
(01) 索引为i的左孩子的索引是 (2*i+1);
(02) 索引为i的左孩子的索引是 (2*i+2);
(03) 索引为i的父结点的索引是 floor((i-1)/2);

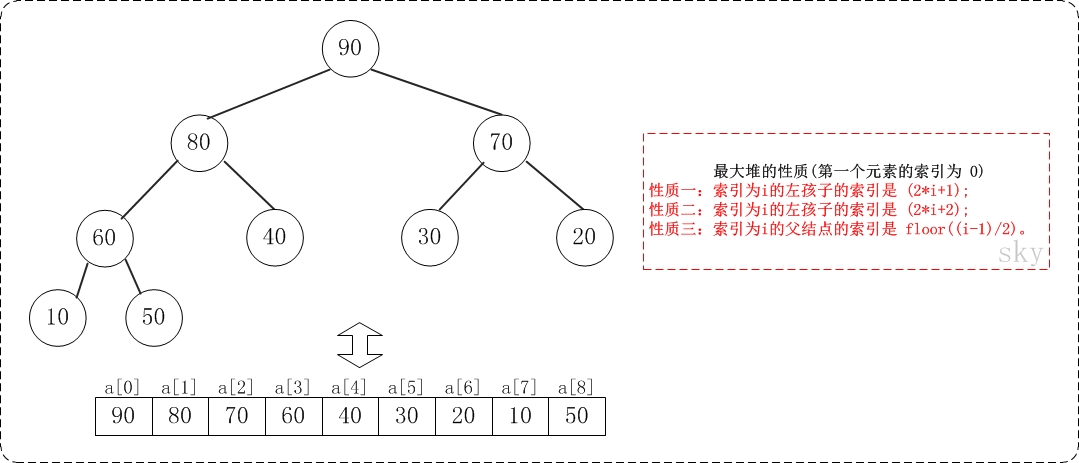
假设"第一个元素"在数组中的索引为 1 的话，则父节点和子节点的位置关系如下：
(01) 索引为i的左孩子的索引是 (2*i);
(02) 索引为i的左孩子的索引是 (2*i+1);
(03) 索引为i的父结点的索引是 floor(i/2);

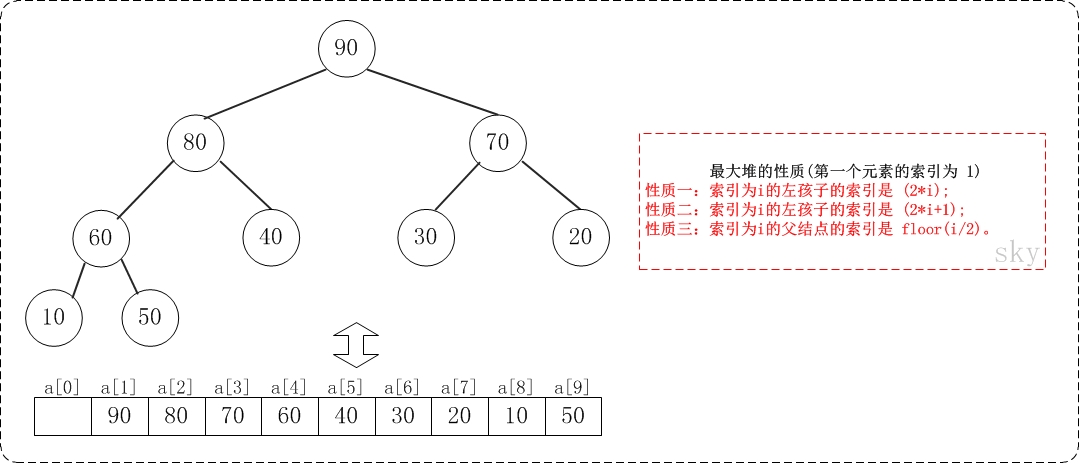
注意：本文二叉堆的实现统统都是采用"二叉堆第一个元素在数组索引为0"的方式！

二叉堆的图文解析

图文解析是以"最大堆"来进行介绍的

1. 基本定义

template <class T>
class MaxHeap{
    private:
        T *mHeap;        // 数据
        int mCapacity;    // 总的容量
        int mSize;        // 实际容量

    private:
        // 最大堆的向下调整算法
        void filterdown(int start, int end);
        // 最大堆的向上调整算法(从start开始向上直到0，调整堆)
        void filterup(int start);
    public:
        MaxHeap();
        MaxHeap(int capacity);
        ~MaxHeap();

        // 返回data在二叉堆中的索引
        int getIndex(T data);
        // 删除最大堆中的data
        int remove(T data);
        // 将data插入到二叉堆中
        int insert(T data);
        // 打印二叉堆
        void print();
};

MaxHeap是最大堆的对应的类。它包括的核心内容是"添加"和"删除"，理解这两个算法，二叉堆也就基本掌握了。下面对它们进行介绍。

2. 添加

假设在最大堆[90,80,70,60,40,30,20,10,50]种添加85，需要执行的步骤如下：

如上图所示，当向最大堆中添加数据时：先将数据加入到最大堆的最后，然后尽可能把这个元素往上挪，直到挪不动为止！
将85添加到[90,80,70,60,40,30,20,10,50]中后，最大堆变成了[90,85,70,60,80,30,20,10,50,40]。

/*
 * 最大堆的向上调整算法(从start开始向上直到0，调整堆)
 *
 * 注：数组实现的堆中，第N个节点的左孩子的索引值是(2N+1)，右孩子的索引是(2N+2)。
 *
 * 参数说明：
 *     start -- 被上调节点的起始位置(一般为数组中最后一个元素的索引)
 */
template <class T>
void MaxHeap<T>::filterup(int start)
{
    int c = start;            // 当前节点(current)的位置
    int p = (c-)/;        // 父(parent)结点的位置
    T tmp = mHeap[c];        // 当前节点(current)的大小

    while(c > )
    {
        if(mHeap[p] >= tmp)
            break;
        else
        {
            mHeap[c] = mHeap[p];
            c = p;
            p = (p-)/;
        }
    }
    mHeap[c] = tmp;
}

/*
 * 将data插入到二叉堆中
 *
 * 返回值：
 *     0，表示成功
 *    -1，表示失败
 */
template <class T>
int MaxHeap<T>::insert(T data)
{
    // 如果"堆"已满，则返回
    if(mSize == mCapacity)
        return -;

    mHeap[mSize] = data;        // 将"数组"插在表尾
    filterup(mSize);    // 向上调整堆
    mSize++;                    // 堆的实际容量+1

    return ;
}

insert(data)的作用：将数据data添加到最大堆中。当堆已满的时候，添加失败；否则data添加到最大堆的末尾。然后通过上调算法重新调整数组，使之重新成为最大堆。

3. 删除

假设从最大堆[90,85,70,60,80,30,20,10,50,40]中删除90，需要执行的步骤如下：

如上图所示，当从最大堆中删除数据时：先删除该数据，然后用最大堆中最后一个的元素插入这个空位；接着，把这个“空位”尽量往上挪，直到剩余的数据变成一个最大堆。
从[90,85,70,60,80,30,20,10,50,40]删除90之后，最大堆变成了[85,80,70,60,40,30,20,10,50]。

注意：考虑从最大堆[90,85,70,60,80,30,20,10,50,40]中删除60，执行的步骤不能单纯的用它的字节点来替换；而必须考虑到"替换后的树仍然要是最大堆"！

/*
 * 最大堆的向下调整算法
 *
 * 注：数组实现的堆中，第N个节点的左孩子的索引值是(2N+1)，右孩子的索引是(2N+2)。
 *
 * 参数说明：
 *     start -- 被下调节点的起始位置(一般为0，表示从第1个开始)
 *     end   -- 截至范围(一般为数组中最后一个元素的索引)
 */
template <class T>
void MaxHeap<T>::filterdown(int start, int end)
{
    int c = start;          // 当前(current)节点的位置
    int l = *c + ;     // 左(left)孩子的位置
    T tmp = mHeap[c];    // 当前(current)节点的大小

    while(l <= end)
    {
        // "l"是左孩子，"l+1"是右孩子
        if(l < end && mHeap[l] < mHeap[l+])
            l++;        // 左右两孩子中选择较大者，即mHeap[l+1]
        if(tmp >= mHeap[l])
            break;        //调整结束
        else
        {
            mHeap[c] = mHeap[l];
            c = l;
            l = *l + ;
        }
    }
    mHeap[c] = tmp;
}

/*
 * 删除最大堆中的data
 *
 * 返回值：
 *      0，成功
 *     -1，失败
 */
template <class T>
int MaxHeap<T>::remove(T data)
{
    int index;
    // 如果"堆"已空，则返回-1
    if(mSize == )
        return -;

    // 获取data在数组中的索引
    index = getIndex(data);
    if (index==-)
        return -;

    mHeap[index] = mHeap[--mSize];    // 用最后元素填补
    filterdown(index, mSize-);        // 从index位置开始自上向下调整为最大堆

    return ;
}

本文来自http://www.cnblogs.com/skywang12345/p/3610382.html