Python实现汉诺塔问题的可视化（以动画的形式展示移动过程）

学习Python已经有一段时间了，也学习了递归的方法，而能够实践该方法的当然就是汉诺塔问题了，但是这次我们不只是要完成对汉诺塔过程的计算，还要通过turtle库来体现汉诺塔中每一层移动的过程。

一、设计一个类（Class）

类(Class):用来描述具有相同的属性和方法的对象的集合。它定义了该集合中每个对象所共有的属性和方法。对象是类的实例。

下面是此程序需用到的类（Class）代码：

 class Stack:
     def __init__(self):
         self.items = []
     def isEmpty(self):
         return len(self.items) == 0
     def push(self, item):
         self.items.append(item)
     def pop(self):
         return self.items.pop()
     def peek(self):
         if not self.isEmpty():
             return self.items[len(self.items) - 1]
     def size(self):
         return len(self.items)

二、设计汉诺塔的底座

为了还原汉诺塔的移动过程，增强可视化程度，我们给它加上三个底座，代码如下：

 def drawpole_3():#画出汉诺塔的poles
     t = turtle.Turtle()
     t.hideturtle()
     def drawpole_1(k):
         t.up()
         t.pensize(10)
         t.speed(100)
         t.goto(400*(k-1), 100)
         t.down()
         t.goto(400*(k-1), -100)
         t.goto(400*(k-1)-20, -100)
         t.goto(400*(k-1)+20, -100)
     drawpole_1(0)#画出汉诺塔的poles[0]
     drawpole_1(1)#画出汉诺塔的poles[1]
     drawpole_1(2)#画出汉诺塔的poles[2]

三、制造汉诺塔的盘子

汉诺塔当然少不了盘子了，我们要写一段代码来绘制若干个盘子，代码如下：

 def creat_plates(n):#制造n个盘子
     plates=[turtle.Turtle() for i in range(n)]
     for i in range(n):
         plates[i].up()
         plates[i].hideturtle()
         plates[i].shape("square")
         plates[i].shapesize(1,8-i)
         plates[i].goto(-400,-90+20*i)
         plates[i].showturtle()
     return plates

四、制造一个底座的栈

栈：栈作为一种数据结构，是一种只能在一端进行插入和删除操作。它按照先进后出的原则存储数据，先进入的数据被压入栈底，最后的数据在栈顶，需要读数据的时候从栈顶开始弹出数据（最后一个数据被第一个读出来）。

此处使用的栈并非Python中真正意义上的栈，而是与之意思相仿的说法，我们都知道，汉诺塔必须将最上的盘子取走方可移动第二层的盘子，以此类推，不移动上方的盘子，就无法移动下方的盘子，废话不多说，来看看这个代码吧：

 def pole_stack():#制造poles的栈
     poles=[Stack() for i in range(3)]
     return poles

五、设计移动盘子的代码

准备完前面的工作，现在就要开始移动盘子了，代码如下：

 def moveDisk(plates,poles,fp,tp):#把poles[fp]顶端的盘子plates[mov]从poles[fp]移到poles[tp]
     mov=poles[fp].peek()
     plates[mov].goto((fp-1)*400,150)
     plates[mov].goto((tp-1)*400,150)
     l=poles[tp].size()#确定移动到底部的高度（恰好放在原来最上面的盘子上面）
     plates[mov].goto((tp-1)*400,-90+20*l)

六、设计操控盘子移动方向的代码

可以移动盘子了当然还不够，只是胡乱地移动无法解决汉诺塔问题，我们要让盘子向着能够解决问题的方向移动，代码如下：

 def moveTower(plates,poles,height,fromPole, toPole, withPole):#递归放盘子
     if height >= 1:
         moveTower(plates,poles,height-1,fromPole,withPole,toPole)
         moveDisk(plates,poles,fromPole,toPole)
         poles[toPole].push(poles[fromPole].pop())
         moveTower(plates,poles,height-1,withPole,toPole,fromPole)

七、调用

终于完成了全部准备工作，现在就来调用函数，让他们一起发挥作用吧！

 import turtle

 class Stack:
     def __init__(self):
         self.items = []
     def isEmpty(self):
         return len(self.items) == 0
     def push(self, item):
         self.items.append(item)
     def pop(self):
         return self.items.pop()
     def peek(self):
         if not self.isEmpty():
             return self.items[len(self.items) - 1]
     def size(self):
         return len(self.items)

 def drawpole_3():#画出汉诺塔的poles
     t = turtle.Turtle()
     t.hideturtle()
     def drawpole_1(k):
         t.up()
         t.pensize(10)
         t.speed(100)
         t.goto(400*(k-1), 100)
         t.down()
         t.goto(400*(k-1), -100)
         t.goto(400*(k-1)-20, -100)
         t.goto(400*(k-1)+20, -100)
     drawpole_1(0)#画出汉诺塔的poles[0]
     drawpole_1(1)#画出汉诺塔的poles[1]
     drawpole_1(2)#画出汉诺塔的poles[2]

 def creat_plates(n):#制造n个盘子
     plates=[turtle.Turtle() for i in range(n)]
     for i in range(n):
         plates[i].up()
         plates[i].hideturtle()
         plates[i].shape("square")
         plates[i].shapesize(1,8-i)
         plates[i].goto(-400,-90+20*i)
         plates[i].showturtle()
     return plates

 def pole_stack():#制造poles的栈
     poles=[Stack() for i in range(3)]
     return poles

 def moveDisk(plates,poles,fp,tp):#把poles[fp]顶端的盘子plates[mov]从poles[fp]移到poles[tp]
     mov=poles[fp].peek()
     plates[mov].goto((fp-1)*400,150)
     plates[mov].goto((tp-1)*400,150)
     l=poles[tp].size()#确定移动到底部的高度（恰好放在原来最上面的盘子上面）
     plates[mov].goto((tp-1)*400,-90+20*l)

 def moveTower(plates,poles,height,fromPole, toPole, withPole):#递归放盘子
     if height >= 1:
         moveTower(plates,poles,height-1,fromPole,withPole,toPole)
         moveDisk(plates,poles,fromPole,toPole)
         poles[toPole].push(poles[fromPole].pop())
         moveTower(plates,poles,height-1,withPole,toPole,fromPole)

 myscreen=turtle.Screen()
 drawpole_3()
 n=int(input("请输入汉诺塔的层数并回车:\n"))
 plates=creat_plates(n)
 poles=pole_stack()
 for i in range(n):
     poles[0].push(i)
 moveTower(plates,poles,n,0,2,1)
 myscreen.exitonclick()

八、效果

首先输入一下我们想测试的汉诺塔层数，为节省时间我就选择了3层

下面是移动过程

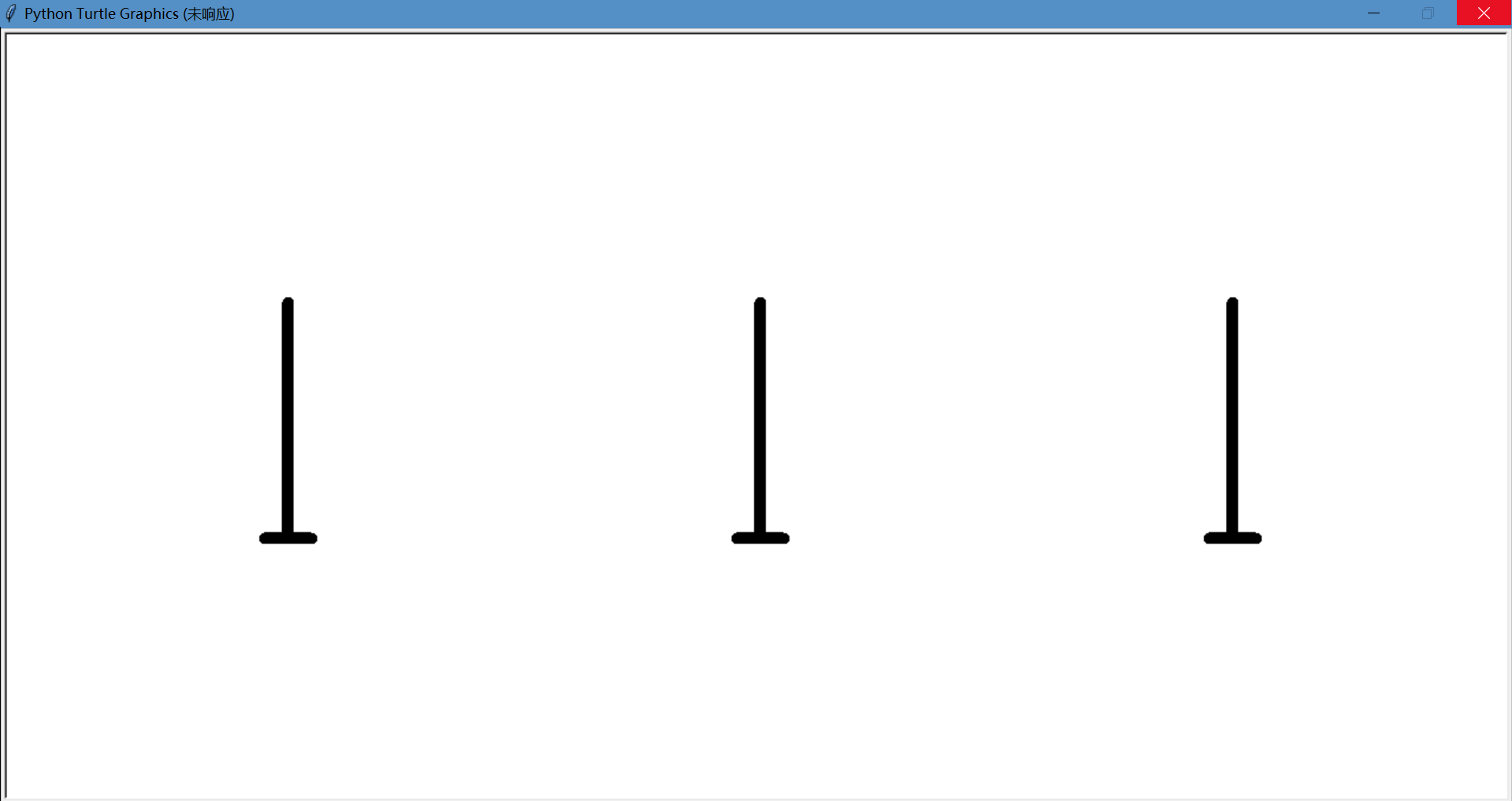
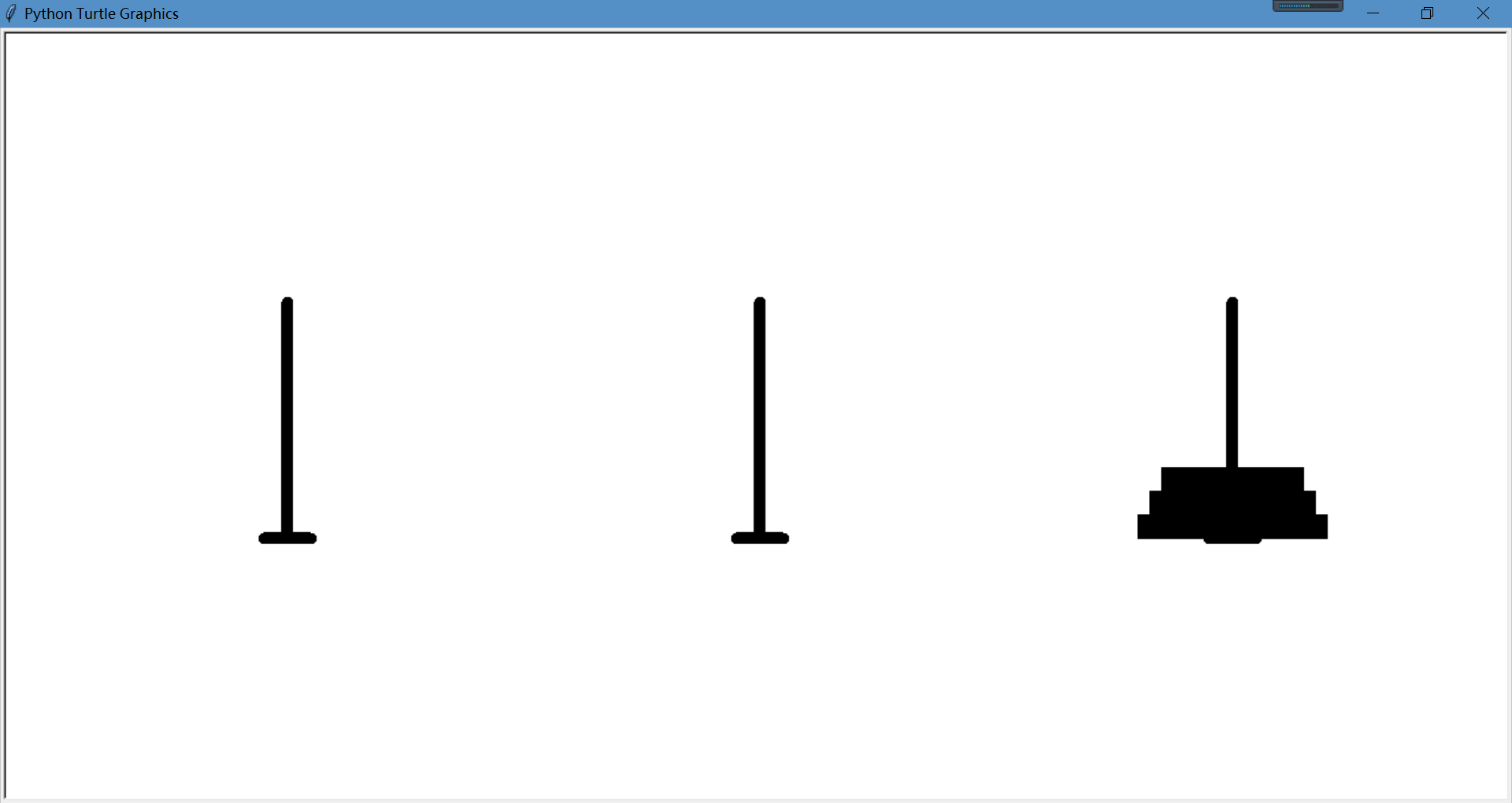
看来效果还不错，这样汉诺塔的可视化就实现啦！