hdu 3486 Interviewe (RMQ+二分)

Interviewe

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 4543    Accepted Submission(s): 1108

Problem Description

YaoYao has a company and he wants to employ m people recently. Since his company is so famous, there are n people coming for the interview. However, YaoYao is so busy that he has no time to interview them by himself. So he decides to select exact m interviewers for this task.
YaoYao decides to make the interview as follows. First he queues the interviewees according to their coming order. Then he cuts the queue into m segments. The length of each segment is 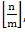, which means he ignores the rest interviewees (poor guys because they comes late). Then, each segment is assigned to an interviewer and the interviewer chooses the best one from them as the employee.
YaoYao’s idea seems to be wonderful, but he meets another problem. He values the ability of the ith arrived interviewee as a number from 0 to 1000. Of course, the better one is, the higher ability value one has. He wants his employees good enough, so the sum of the ability values of his employees must exceed his target k (exceed means strictly large than). On the other hand, he wants to employ as less people as possible because of the high salary nowadays. Could you help him to find the smallest m?

 

Input

The input consists of multiple cases.
In the first line of each case, there are two numbers n and k, indicating the number of the original people and the sum of the ability values of employees YaoYao wants to hire (n≤200000, k≤1000000000). In the second line, there are n numbers v1, v2, …, vn (each number is between 0 and 1000), indicating the ability value of each arrived interviewee respectively.
The input ends up with two negative numbers, which should not be processed as a case.

 

Output

For each test case, print only one number indicating the smallest m you can find. If you can’t find any, output -1 instead.

 

Sample Input

11 300

7 100 7 101 100 100 9 100 100 110 110

-1 -1

 

Sample Output

3

Hint

We need 3 interviewers to help YaoYao. The first one interviews people from 1 to 3, the second interviews people from 4 to 6,
and the third interviews people from 7 to 9. And the people left will be ignored. And the total value you can get is 100+101+100=301>300.

 

Source

2010 ACM-ICPC Multi-University Training Contest（5）——Host by BJTU

 

Recommend

zhengfeng   |   We have carefully selected several similar problems for you:  2888 3478 3487 3480 3485 

 

题意：

给出n个数，分成m段，每段取一个最大的，问m最小为多少时每段取到的最大的数的和大于K。

RMQ+二分：

时间卡很紧，800+ms  C++飘过。

这题有个trap，坑了我很久的trap。

RMQ+二分其实很快就写好了，问题是卡在数据上，先看看数据

11 300
7 100 7 101 100 100 9 100 100 110 110

10 1500
1 1 1 1 1000 1000 1 1 1 1

8 201
100 100 100 100 101 100 100 100

很明显第一组数据输出的是3，题目有解释。

到第二组数据呢？本来应该输出2才合理，可是运行结果却是输出了6.

第三组也是输出2才合理，可结果是输出了3。

个人觉得是数据有点问题，题目也有点问题，其实这题用二分过不了才对，因为看第二组和第三组数据可知，数据其实没有单调性。

贴一下代码：

 //781MS    16708K    1338 B    C++
 #include<stdio.h>
 #include<math.h>
 #define N 200005
 int v[N];
 int dp[N][];
 inline int Max(int a,int b)
 {
     return a>b?a:b;
 }
 void init(int n)
 {
     for(int i=;i<=n;i++)
         dp[i][]=v[i];
     for(int j=;j<;j++)
         for(int i=;i+(<<j)-<=n;i++)
             dp[i][j]=Max(dp[i][j-],dp[i+(<<(j-))][j-]);
 }
 inline int RMQ(int l,int r)
 {
     int m=(int)(log(1.0*(r-l+))/log(2.0));
     return Max(dp[l][m],dp[r-(<<m)+][m]);
 }
 inline int getsum(int m,int mm)
 {
     int sum=;
     for(int i=;i+mm-<=m*mm;i+=mm)
        sum+=RMQ(i,i+mm-);
     return sum;
 }
 int main(void)
 {
     int n,k;
     while(scanf("%d%d",&n,&k)!=EOF)
     {
         if(n< || k<) break;
         int sum=;
         int maxn=;
         for(int i=;i<=n;i++){
             scanf("%d",&v[i]);
             sum+=v[i];
             maxn=Max(maxn,v[i]);
         }
         if(sum<=k){
             puts("-1");continue;
         }
         if(maxn>k){
             puts("");continue;
         }
         init(n);
         int l=,r=n,mid;
         while(l!=r){
             mid=(l+r)/;
             int ans=getsum(mid,n/mid);
             printf("*%d %d\n",mid,ans);
             if(ans<=k) l=mid+;
             else r=mid;
         }
         printf("%d\n",l);
     }
     return ;
 }
 /*

 11 300
 7 100 7 101 100 100 9 100 100 110 110

 10 1500
 1 1 1 1 1000 1000 1 1 1 1

 8 201
 100 100 100 100 101 100 100 100

 */