多目标规划——fgoalattain

多目标规划

多个目标函数，之间可以用他们的重要程度分析，来一次进行这个序贯算法，当然也可以无限逼近的方案——​

clc,clear;
% 约束
a = [- -
      - -

       ];
b = [-
    -

    ];
% 求两次单一目标函数
c1 = [- - - -];
c2 = [   ];
​
% 单一目标值 g1,g2
[x1,g1] = linprog(c1,a,b,[],[],zeros(,));
[x2,g2] = linprog(c2,a,b,[],[],zeros(,));
​
% 组合多目标规划,fgoalattain
g3 = [g1
    g2];
​
[x,fval] = fgoalattain('Fun',rand(,),g3,abs(g3),a,b,[],[],zeros(,));

如何设置权重weight呢？

比如：

 

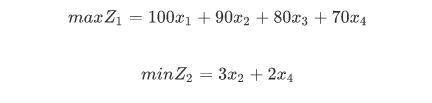
第一个式子的重要程度是20%，第二个式子的重要程度是80%。

哈哈，想到这里，其实是错误的，可以有这种想法，但是我们的多目标规划问题，就是要无限逼近这两个目标，不存在说两个式子哪个重要。哪个重要，还不如用我们的之前的那个序贯算法呢。看看MATLAB官方文档是如何说的这个参数。

A weighting vector to control the relative underattainment or overattainment of the objectives in fgoalattain. When the values of goal are all nonzero, to ensure the same percentage of under- or overattainment of the active objectives, set the weighting function to abs(goal). (The active objectives are the set of objectives that are barriers to further improvement of the goals at the solution.)Note Setting a component of the weight vector to zero will cause the corresponding goal constraint to be treated as a hard constraint rather than as a goal constraint. An alternative method to set a hard constraint is to use the input argument nonlcon.

When the weighting function weight is positive, fgoalattain attempts to make the objectives less than the goal values. To make the objective functions greater than the goal values, set weight to be negative rather than positive. To make an objective function as near as possible to a goal value, use theEqualityGoalCount option and put that objective as the first element of the vector returned by fun (see the preceding description of fun and options).