【莫比乌斯反演+分块】BZOJ1101-[POI2007]Zap

【题目大意】

对于给定的整数a,b和d，有多少正整数对x,y，满足x<=a，y<=b，并且gcd(x,y)=d。

【思路】

前面的思路同HDU1695

不过不同的是这道题中(a,b)和(b,a)算作同一种情况，不需要再减去重复的情况。

这道题运用了分块加快效率。我们可以注意到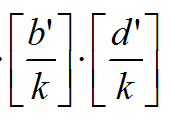是相同的，b'(b'/i)b表示和当前商相同的最后一位[b'/d]，d'(d'/i)同理,pos为两者中较小的一个。我们预处理Miu的前缀和，就可以将一样的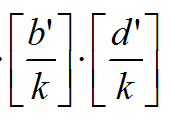*（sum[pos]-pos[k-1]）即可！

？？BZOJ一定要用printf%lld，cout会RE??

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 typedef long long ll;
 const int MAXN=+;
 const int INF=0x7ffffff;
 int a,b,d;
 int miu[MAXN];
 int miu_sum[MAXN];

 void get_miu(int maxn)
 {
     int prime[MAXN],pnum=;
     memset(miu_sum,,sizeof(miu_sum));
     miu[]=miu_sum[]=;
     for (int i=;i<maxn;i++) miu[i]=-INF;
     for (int i=;i<maxn;i++)
     {
         if (miu[i]==-INF)
         {
             miu[i]=-;
             prime[++pnum]=i;
         }
         for (int j=;j<=pnum;j++)
         {
             if (i*prime[j]>=maxn) break;
             if (i%prime[j]==) miu[i*prime[j]]=;
                 else miu[i*prime[j]]=-miu[i];
         }
         miu_sum[i]=miu_sum[i-]+miu[i];
     }
 }

 ll get_ans(int a,int b,int d)
 {
     int ub=min(a,b),pos;
     ll ans=;
     for (int i=;i<=ub;i=pos+)
     {
         pos=min(a/(a/i),b/(b/i));
         ans+=(ll)(miu_sum[pos]-miu_sum[i-])*(a/i)*(b/i);
     }
     return ans;
 }

 int main()
 {
     int T;
     scanf("%d",&T);
     get_miu(MAXN-);
     for (int i=;i<T;i++)
     {
         scanf("%d%d%d",&a,&b,&d);
         a/=d;b/=d;
         printf("%lld\n",get_ans(a,b,d));
     }
 }