Covered Points Count（思维题）

C. Covered Points Count

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given nn segments on a coordinate line; each endpoint of every segment has integer coordinates. Some segments can degenerate to points. Segments can intersect with each other, be nested in each other or even coincide.

Your task is the following: for every k∈[1..n]k∈[1..n], calculate the number of points with integer coordinates such that the number of segments that cover these points equals kk. A segment with endpoints lili and riri covers point xx if and only if li≤x≤rili≤x≤ri.

Input

The first line of the input contains one integer nn (1≤n≤2⋅1051≤n≤2⋅105) — the number of segments.

The next nn lines contain segments. The ii-th line contains a pair of integers li,rili,ri (0≤li≤ri≤10180≤li≤ri≤1018) — the endpoints of the ii-th segment.

Output

Print nn space separated integers cnt1,cnt2,…,cntncnt1,cnt2,…,cntn, where cnticnti is equal to the number of points such that the number of segments that cover these points equals to ii.

Examples

input

Copy

3
0 3
1 3
3 8

output

Copy

6 2 1 

input

Copy

3
1 3
2 4
5 7

output

Copy

5 2 0 

Note

The picture describing the first example:

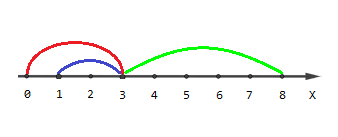
Points with coordinates [0,4,5,6,7,8][0,4,5,6,7,8] are covered by one segment, points [1,2][1,2] are covered by two segments and point [3][3] is covered by three segments.

The picture describing the second example:

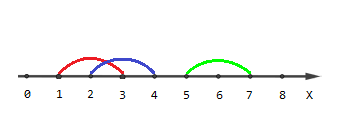
Points [1,4,5,6,7][1,4,5,6,7] are covered by one segment, points [2,3][2,3] are covered by two segments and there are no points covered by three segments.

这题坑点比较多，没有开LLwa一发 ，数组开小了又wa一发 难受

细节方面很多都没有注意到

　

　这题是纯思维题 把每一个区间分为两个点一个左端点一个右端点

进行排序一下，就出来了

从左往右扫一遍经历一次左端点就加一，经历一次又端点就减一

这个规律看图一下就出来了

 #include <bits/stdc++.h>
 using namespace std;
 const int maxn = 4e5 + ;
 typedef long long LL;
 struct node {
     LL x, y;
     node (LL x, LL y) : x(x), y(y) {}
     node () {}
 } qu[maxn];
 int cmp(node a, node b) {
     if (a.x == b.x) return a.y > b.y;
     return a.x < b.x;
 }
 LL ans[maxn];
 int main() {
     LL n,k=,a,b;
     scanf("%lld", &n);
     for (int i =  ; i < n ; i++) {
         scanf("%lld%lld",&a,&b);
         qu[k++] = node(a, );
         qu[k++] = node(b + , -);
     }
     sort(qu, qu + k, cmp);
     LL temp = ;
     for(int i =  ; i < k-  ; i++ ) {
         temp += qu[i].y;
         if (qu[i].x != qu[i + ].x) ans[temp]+= qu[i + ].x - qu[i].x;
     }
     for (int i =  ; i <=n ; i++)
         printf("%lld ", ans[i]);
     printf("\n");
     return ;
 }