ML 徒手系列 拉格朗日乘子法

　　拉格朗日乘子法是解决极值问题的方法。

　　本方法是计算多元函数在约束条件下的极值问题的方法。

1、多元函数与约束问题

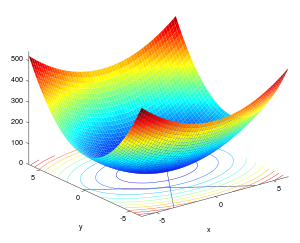
　　如下图所示，f(x,y)为多元函数，g(x,y)=c为约束条件。目的是计算在约束条件下多元函数的极值。

　　虚线为f(x,y)=d d取不同的值时，将原始图像投影到xy平面时的等高线，在等高线上的f函数值相等；

　　淡蓝色实线为g(x,y)为xy平面的曲线，对应于不同的(x,y)。比如g(x,y)=x+y=1,即x+y=1为约束条件。

　　　　　　　　　　　　

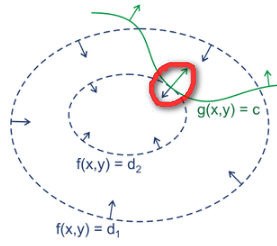
　　那么怎样去寻找极值点？

　　思路：沿着g(x,y)曲线不断前进，找到与g(x,y)与等高线的交点，所有的交点中的极值，即为需要求得的极值。如上图红色圈所示。

　　此时极值点满足的条件：g(x,y)与极值点所在的等高线是相切的。所以满足

　　根据以上原理，构建拉格朗日函数：（此时用g(x,y)代替[g(x,y)-c]）

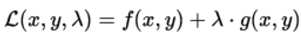
　　L对x,y,λ分别求偏导，并且偏导其偏导满足：

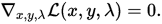
　　偏导分别满足：

　　

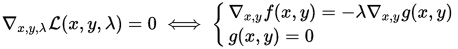
　　根据得到的偏导等式，求得x,y的值，即可得到f(x,y)的极值。

　　同样当g(x,y)<0时，等高线与约束函数的图像变成了等高线与某一块区域的集合。此时求极值时，直接求f(x,y)对x,y的偏导数，得到极值。

　　等价于将λ置为0时，求L对x,y求偏导。上述是拉格朗日乘子法的来源。

2、约束条件的扩展

　　第一部分讲解了一个约束条件，而实际中通常会用到多个约束条件。当引入下列约束条件时：

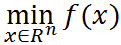
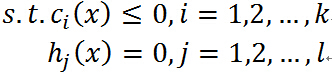
　　即要求f₀(x)的极值，其约束条件为f_i(x) h_i(x).此时的拉格朗日函数为：

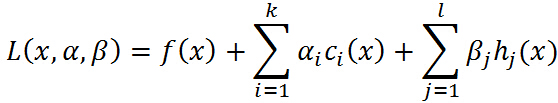
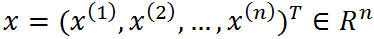
　　其中ª ß为拉格朗日乘子。并且ª>0,满足第一部分所阐述的λ的条件。　

　　上述条件表述为KKT条件：

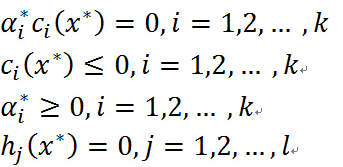
　　固定变量x,求L关于ª ß的最大值：

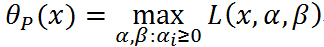
　　并且有：

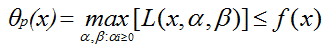
　　对θ_p求极小值可得：

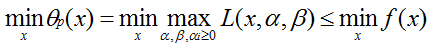
　　此时，求θ_p极小值与原始问题即求f(x)的极小值等价。

　　定义原始问题的最优：

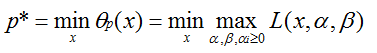
　　引入对偶问题：

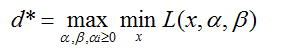
　　可以证明:

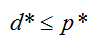
　　对偶问题证明：

　　

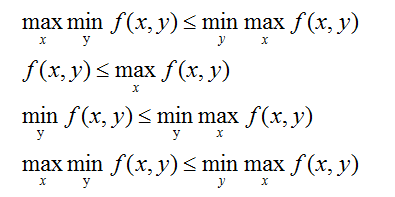
　　使用上述条件：

　　1、对L取关于变量x的偏导

　　2、通过偏导式子求出x关于ª ß的表达式

　　3、将ª ß的表达式代入L

　　4、得到max(L)关于ª ß的表达式

　　5、通过其他约束条件求出最终的极值点

　　举例：

　　SVM

　　对偶问题满足等号的条件：

　　KKT条件中的约束不等式为凸函数，等式为仿射函数，且可行域存在严格满足约束条件的点。