(六) 6.2 Neurons Networks Backpropagation Algorithm

今天得主题是BP算法。大规模的神经网络可以使用batch gradient descent算法求解，也可以使用 stochastic gradient descent 算法，求解的关键问题在于求得每层中每个参数的偏导数，BP算法正是用来求解网络中参数的偏导数问题的。

先上一张吊炸天的图，可以看到BP的工作原理：

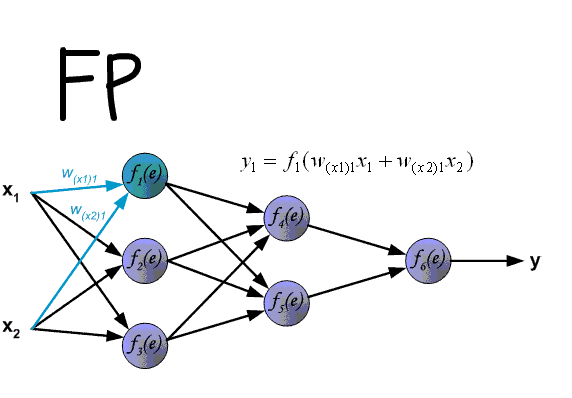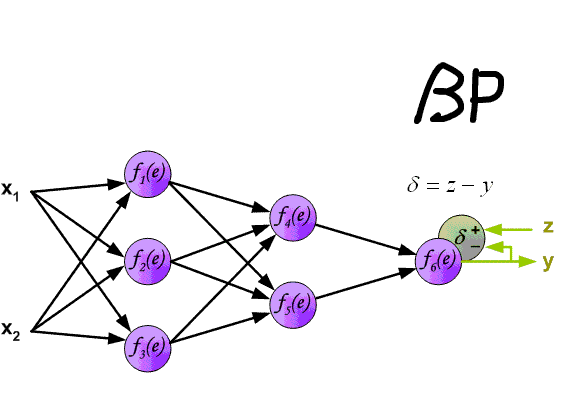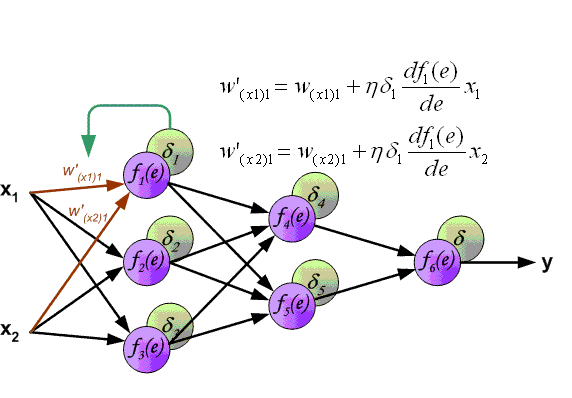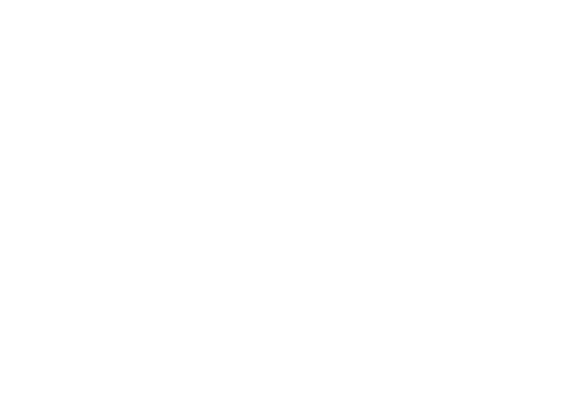
下面来看BP算法，用m个训练样本集合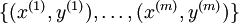来train一个神经网络，对于该模型，首先需要定义一个代价函数，常见的代价函数有以下几种：

1）0-1损失函数：（0-1 loss function）

2）平方损失函数：（quadratic loss function）

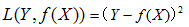
3）绝对值损失函数：（absolute loss function）

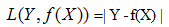
4）负log损失函数（log loss function）

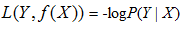
损失函数的意义在于，假设函数（hypothesis function，即模型）的输出与数据标签的值月接近，损失函数越小。反之损失函数越大，这样减小损失函数的值，来求得最优的参数即可，最后将最优的参数带入带假设函数中，即可求得最终的最优的模型。

在Neurons Network中，对于一个样本（x，y），其损失函数可表示为　　

　　

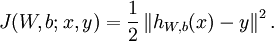
上式这种形式是平方损失函数（注意若采用交叉熵损失则与此损失形式不一样），对于所有的m个样本，对于所有训练数据，总的损失函数为：

　　

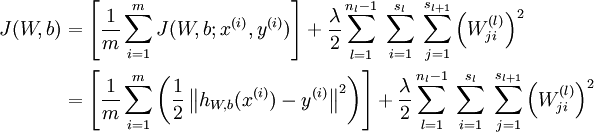
上式中第一项为均方误差项，第二项为正则化项，用来限制权重W的大小，防止over-fitting，也即贝叶斯学派所说的给参数引入一个高斯先验的MAP（极大化后验）方法。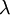为正则项的参数，用来控制两项的相对重要性， 比如若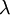很大时，参数W，b必须很小才能使得最终的损失函数J(W，b) 很小。

常见的分类或者回归问题，都可以用这个损失函数，注意分类时标签y是离散值，回归时对于sigmod函数y为(0,1)之间的连续值。对于tanh为(-1,1)之间的值。

BP算法的目标就是求得一组最优的W、b ，使得损失函数 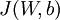的值最小

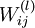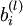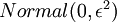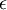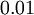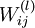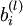首先将每个参数  和 初始化为一个很小的随机值（比如说，使用正态分布  生成的随机值，其中  设置为  ），然后使用批梯度下降算法来优化 和 的值，因为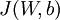 是非凸函数，即存在不止一个极值点，梯度下降算法很可能会收敛到局部极值处，但通常效果很不错（在浅层网络中，比如说三层），需要强调的是要将参数随机初始化，而不是全部置0，如果所有参数都用相同的值作为初始值，那么所有隐藏层单元最终会得到与输入值有关的、相同的函数（也就是说，对于所有hidden unit 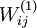，都会取相同的值，那么对于任何输入  都会有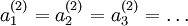： ），随机初始化会消除这种对称效果。

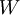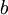批梯度下降算法中，每一次迭代都按照如下公式对参数  和 进行更新：

　　

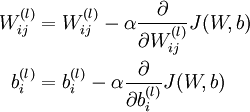
其中J(W，b)包含了所有的样本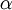， 是学习速率，对于多层神经网络，如何计算每一层参数的偏导数是关键问题，BP算法正使用来计算每一项的偏导数的。

首先来看对于单个样例，参数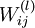 和 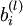 的偏导数分别为  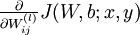和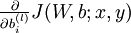 

有了单个样例的偏导数后，根据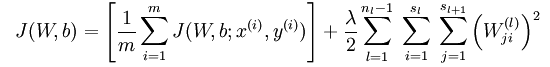，就可以很好求出损失函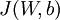数  的偏导数：

　　

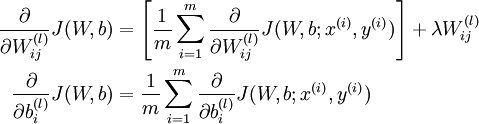
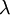 并不作用于bais unit b，所以第二个式子中没有第二项。

先看如下的式子，l+1层的输入等于l层的加权输出求和，即

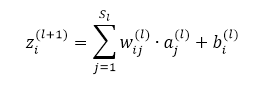
课件hidden layer的输入z为参数的方程，为了求解对每个样本中参数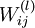 和 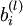 的偏导数，可以用根据链式求导法则有:

 

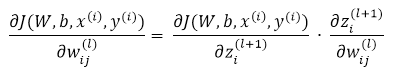
我们把上边的第一项称为残差，有了以上链式求导的思想，为了求得各个参数的偏导数，我们需要求得每一层的每个单元的残差。下面反向传播算法的思路：

1）给定 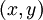，我们首先进行“前向传导”，计算出网络中所有的激活值，包括  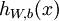的输出值

2）对第  层的每个节点 ，计算出其“残差” 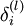，该残差表明节点对最终输出值的残差产生多少影响

3）对于最终的输出节点，直接算出网络产生的激活值与实际值之间的差距，将这个差距定义为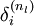 

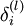4）对于隐藏单元，将第  层节点的残差的加权平均值计算 ，这些节点以  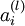作为输入到  层

下面将给出反向传导算法的细节：

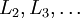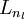1）进行前馈传导计算，利用前向传导公式，得到  直到输出层  的激活值。

2）对于第 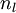 层（输出层）的每个输出单元 ，我们根据以下公式计算残差：

　　
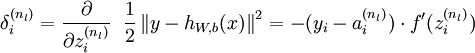
推倒：

　　

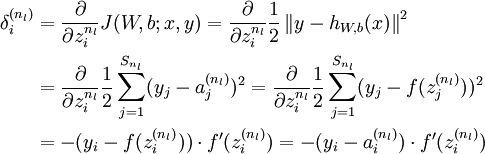
3）对 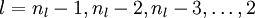 的各个层，第  层的第  个节点的残差计算方法如下：

　　

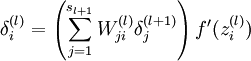
有了最后一层的层差，可以计算前一层的残差：

　　

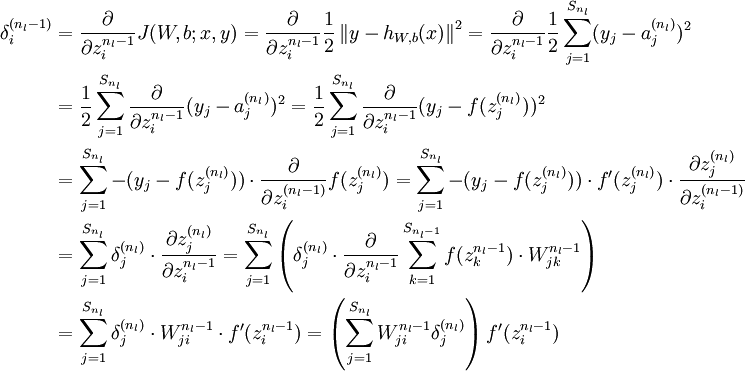
4)将上式中的 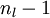 与 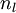 的关系替换为  与  的关系，就可以得到：

5)根据链式求导法则，计算方法如下：

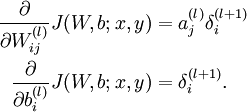
其中，第二项的计算公式如下：

根据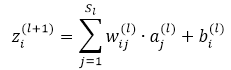，有：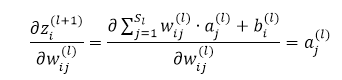

 

概括一下整个算法：

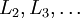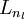1）进行前馈传导计算，利用前向传导公式，得到 直到输出层  的激活值。

2）对输出层（第 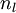 层），计算：

　　

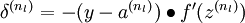
3）对于 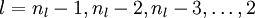 的各层，计算：

　　

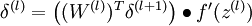
4）计算最终需要的偏导数值：

　　

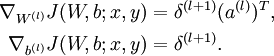
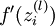指的注意的是在以上的第2步和第3步中，我们需要为每一个 单元 值计算其 。假设 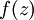 是sigmoid函数，f'(z)=f(z)*(1-f(z)),并且我们已经在前向传导运算中得到了 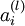。那么，使用我们早先推导出的 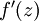表达式，就可以计算得到 。

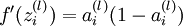经过以上步骤，已经可以求出每个参数的偏导数，下一步就是更新参数，即使得参数沿梯度方向下降，下面给出梯度下降算法伪代码：

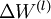 是一个与矩阵  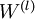维度相同的矩阵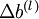， 是一个与 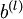 维度相同的向量。注意这里“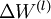”是一个矩阵，而不是“ 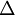与 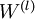 相乘”。下面，我们实现批量梯度下降法中的一次迭代：

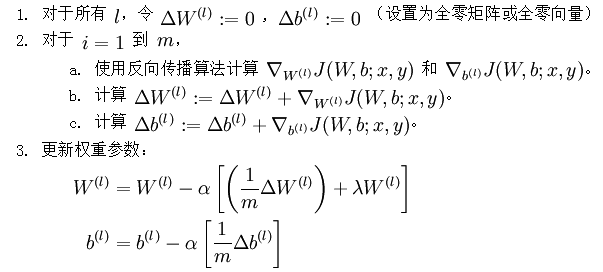
不断更新W，b的值，直到W，b不再变化为止，即网络达到收敛。

有机会再补上代码#24！！