（精）题解 guP4878 [USACO05DEC] 布局

差分约束模版题

不过后三个点简直是满满的恶意qwq

这里不说做题思路（毕竟纯模板），只说几个坑点：

1. 相邻的两头牛间必须建边（这点好像luogu没有体现），例如一组数据：

4 1 1

1 4 10

2 3 20

output：-1

若相邻牛未建边，跑出来的结果是10；而事实如图：

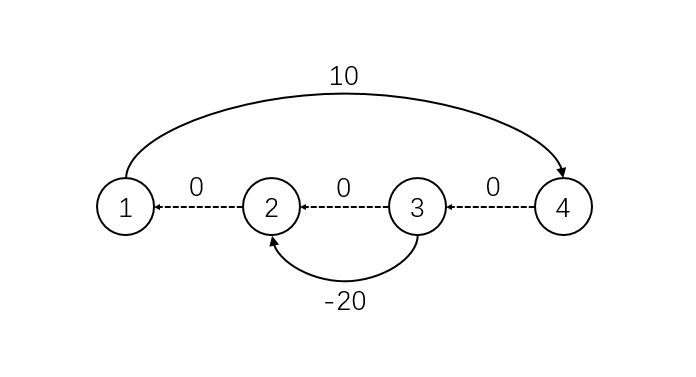
存在负权环。

因此我在代码里写了一条：

for(int i=1;i<n;i++)
{
    add(i+1,i,0);
}

------我是分割线-------

2. 应跑两遍SPFA，一遍从超级源点0判断有无解，一遍从1计算结果。

如果不跑0那一遍，则可能判不出题目原图是否联通或有无负权环（毕竟从点1不一定能到达所有点）。

所以要建边qwq

for(int i=1;i<=n;i++)
{
    add(0,i,0);
}

似乎可以了qwq

AC代码：

//Author:pawn
#include<bits/stdc++.h>
using namespace std;
int n,ml,md,a,b,c,fst[10100],nex[50010],v[50010],w[50010],cnt,vis[10100],dis[10100],tim[10100];
queue<int> q;
void add(int a,int b,int c)
{
    nex[++cnt]=fst[a];
    fst[a]=cnt;
    v[cnt]=b;
    w[cnt]=c;
    return ;
}
int spfa(int k)
{
    memset(dis,0x7f/3,sizeof(dis));
    memset(vis,0,sizeof(vis));
    memset(tim,0,sizeof(tim));
    q.push(k);
    dis[k]=0;
    vis[k]=1;
    while(!q.empty())
    {
        int u=q.front();
        //cout<<u<<" ";
        q.pop();
        tim[u]++;
        vis[u]=0;
        if(tim[u]>n)
        return -1;
        for(int i=fst[u];i!=-1;i=nex[i])
        {
            if(dis[v[i]]>dis[u]+w[i])
            {
                dis[v[i]]=dis[u]+w[i];
                if(!vis[v[i]])
                {
                    q.push(v[i]);
                    vis[v[i]]=1;
                }
            }
        }
    }
    /*cout<<endl;
    for(int i=1;i<=n;i++)
    {
        cout<<dis[i]<<" ";
    }*/
    if(dis[n]>1e8)
    return -2;
    return dis[n];
}
int main()
{
    memset(fst,-1,sizeof(fst));
    cin>>n>>ml>>md;
    for(int i=1;i<=ml;i++)
    {
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);
    }
    for(int i=1;i<=md;i++)
    {
        scanf("%d%d%d",&a,&b,&c);
        add(b,a,-c);
    }
    for(int i=1;i<n;i++)
    {
        add(i+1,i,0);
    }
    for(int i=1;i<=n;i++)
    {
        add(0,i,0);
    }
    int sp=spfa(0);
    if(sp<=-1)
    {
    	cout<<sp;
    	return 0;
    }
    else
    {
    	cout<<spfa(1);
    }
    //cout<<" "<<sp;
    return 0;
}
/*
5 1 1
1 5 10
2 3 20
*/
//output:-1

求过qwq