InnoDB 索引详解

1、什么是索引

索引是存储引擎用于快速找到记录的一种数据结构。

2、索引有哪些数据结构

• 顺序查找结构：这种查找效率很低，复杂度为O(n)。大数据量的时候查询效率很低。

• 有序的数据排列：二分查找法又称折半查找法。

  通过一次比较，将查找区间缩小一半。而MySQL中的数据并不是有序的序列。

• 二叉查找树：左子树的键值总是小于根的键值， 右子树的键值总是大于根的键值。通过中序遍历得到的序列是有序序列，但如果二叉查找树构造的不好则跟顺序查找没什么区别

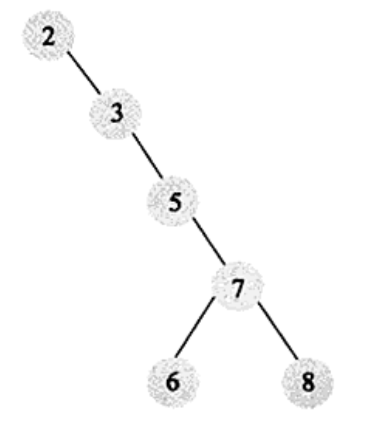
• 平衡二叉树：如果需要二叉查找树是平衡的，从而引出平衡二叉树。平衡二叉树首先得满足二叉查找树的定义，其次必须满足任何结点的两个子树的高度的最大差为1。显然上面的树不是平衡二叉树，平衡二叉树示例如下：

  

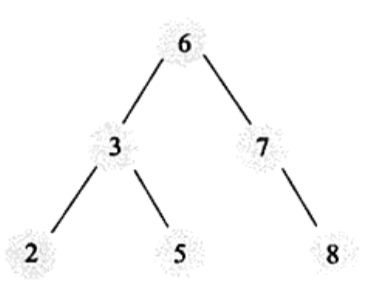
平衡二叉查找树的时间复杂度为O(logN)，查询速度的确很快，但是维护一颗平衡二叉树的代价也是非常大的。通常来说，需要一次或多次左旋和右旋来得到插入或更新后的平衡性。

• B树：B树和平衡二叉树稍有不同的是B树属于多叉树又名平衡多路查找树：

1. 根节点至少有两个子节点（每个节点有M-1个Key， 且以升序排列） 其它节点至少有M/2个子节点

2. 叶子结点都在同一层。

• B+树

B+树是B树的变种，B+树由B树和索引顺序访问方法演化而来(在现实生活中几乎没有使用B树的情况来)。

B+树是为磁盘或其他直接存储辅助设备设计的一种平衡查找树。

　　 在B+树中所有记录结点都是按键值的大小顺序放在同一层的叶子结点上， 由各叶子节点指针进行连接。

所有查询都要查找到叶子节点，查询性能稳定。

所有叶子节点形成有序链表，便于范围查询。每个叶子结点都存有相邻叶子结点的指针，叶子结点本身依关键字的大小自小而大顺序链接（双向链表）

3、Innodb为什么使用B+树做为索引

1. 可以有效的利用系统对磁盘的块读取特性，在读取相同磁盘块的同时，尽可能多的加载索引数据，来提高索引命中效率，从而达到减少磁盘IO的读取次数（局部性原理与磁盘预读）。

2. B+树的磁盘读写代价更低：B+树的内部节点并没有指向关键字具体信息的指针（只有叶子节点存储有），因此其内部节点相对B树更小，如果把所有同一内部节点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多，一次性读入内存的需要查找的关键字也就越多，相对IO读写次数就降低了。

3. B+树的查询效率更稳定。由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。

4. B+树支持范围查询，而B树不支持

4、索引分类

从存储结构上分类：BTree索引、Hash索引、全文索引

从应用上分类：主键索引、唯一索引、组合索引

从物理存储角度：聚集索引和非聚集索引（辅助索引）

下面说说什么是聚集索引， 什么是非聚集索引：

• 聚集索引

按照每张表的主键构建一棵B+树，同时叶子节点中存放的即为整张表的行记录数据。也将聚集索引的叶子节点称为数据页，每个数据页都通过一个双向链表进行链接。

聚集索引对于主键的排序查找 和 范围查找的数据非常快。

• 辅助索引

除了存储了索引列，还存储了叶子节点的指针。