变分贝叶斯学习（variational bayesian learning）及重参数技巧（reparameterization trick）

摘要：常规的神经网络权重是一个确定的值，贝叶斯神经网络（BNN）中，将权重视为一个概率分布。BNN的优化常常依赖于重参数技巧（reparameterization trick），本文对该优化方法进行概要介绍。

论文地址：http://proceedings.mlr.press/v37/blundell15.pdf

网络权重的点估计

常规神经网络可以基于MLE或MAP对权重作点估计。

基于MLE（maximum likelihood estimation）：

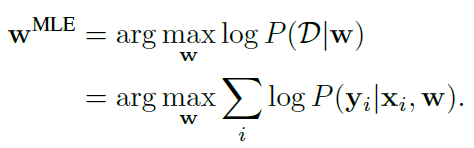
基于MAP（maximum a posteriori）：

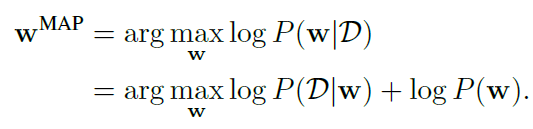
对权重施加先验，等价于进行正则化。如果施加的是高斯先验，相当于进行L2正则，如果是一个laplace先验，相当于L1正则。

贝叶斯方法

贝叶斯推断在给定训练数据的情况下，计算网络参数的后验概率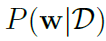，理论上可以通过以下方式对样本标签所服从的分布进行预测：

Hinton等人提出对网络权重的贝叶斯后验分布进行变分估计，变分学习寻找参数θ，来最小化分布q(w|θ）和权重真实后验分布之间的KL距离，这里的参数θ可理解为w所服从分布的参数，比如高斯的μ和σ：

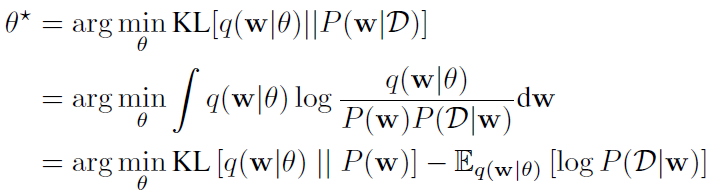
这个loss函数就是变分自由能（variational free energy），也称为期望下界（expected lower bound， ELBO）。

可以将loss函数简记为：

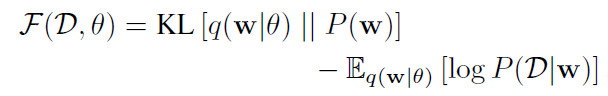损失函数的后半部分代表与数据相关，称之为似然损失，前半部分与先验有关，称为先验损失。该损失也被称为最小描述长度（minimum description length, MDL）

无偏蒙特卡洛梯度

我们使用梯度下降的方式对上述损失进行优化。

在特定的条件下，期望的微分等于微分的期望。

命题1：假设ε服从分布q(ε)，令w = t(θ, ε)，其中t(θ, ε)是一个确定性函数，假如w的边缘密度q(w|θ)满足q(ε) dε = q(w|θ) dw，那么：

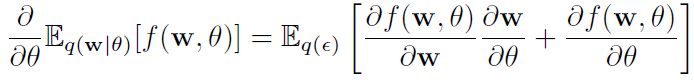
证明：

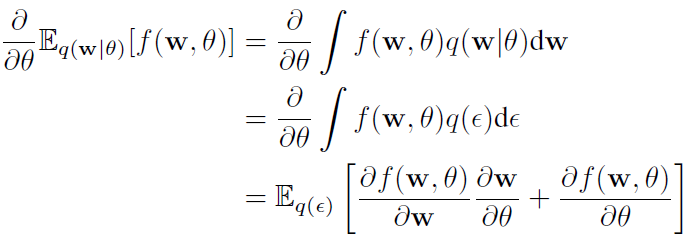
确定性函数 t(θ, ε)将一个随机噪声和变分后验参数转换为一个变分后验。

令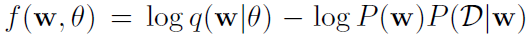，我们可以将命题1用于优化。通过蒙特卡洛采样，可以通过反向传播算法对网络进行优化。

命题1就是所谓的重参数技巧（reparameterization trick）。

变分高斯后验

基于高斯后验的变分学习训练过程如下：

这里就是常规反向传播算法得到的梯度。

基于tensorflow probability的贝叶斯全连接网络示例

import tensorflow as tf
import tensorflow_probability as tfp

model = tf.keras.Sequential([
    tfp.layers.DenseReparameterization(512, activation=tf.nn.relu),
    tfp.layers.DenseReparameterization(10),
])

logits = model(features)
neg_log_likelihood = tf.nn.softmax_cross_entropy_with_logits(
    labels=labels, logits=logits)
kl = sum(model.losses)

# loss由两部分构成：（1）负对数似然（2）参数分布与其先验分布（regularizer）之间的KL距离

loss = neg_log_likelihood + kl

train_op = tf.train.AdamOptimizer().minimize(loss)