《MATLAB从入门到放弃》打通 “矩阵” 障碍

目录：

»   矩阵的生成与大小

 >   简单矩阵的生成

 >  随机矩阵的生成

 >   矩阵的大小

»  矩阵的索引与访问

»  矩阵的拼接与裁剪

>  矩阵的拼接

>  矩阵的裁剪

»  矩阵的运算与操作

>  矩阵的算术运算

>  矩阵的翻转

---

矩阵的生成与大小

简单矩阵的生成

A = [1 2; 3 5; 8 5; 4 6]	空格/逗号表示一列一列，分号/换行表示一行一行
B = 1:2:9	从1到9，每隔2个取一个整数，即1，3，5，7，9  (2可以是整数/小数) 。2不写，默认1
C = zeros (5,6)	5*6全0矩阵
D = ones(5,6)	生成5*6的全1矩阵
E = linspace (4,12,6)	生成4~12之间5个等分的数(小数/整数)。6不写，默认100
F = logspace(1,3,5)	生成5个[10^1 , 10^3]之间的数。5不写，默认50
G = eye(5,6)	生成5行6列对角线是1，其他是0的矩阵 。

 

随机矩阵的生成

A = rand(5,6)	生成[0,1]范围内的5*6的随机小数矩阵
B= rand	只产生一个[0,1]范围内的随机小数矩阵
C=m+(n-m)*rand(a, b)	在[m,n]范围内生成a行b列小数矩阵
D= randi(m,a)	生成[1,m]范围内的a*a整数矩阵
E = randi(a)	生成一个[1,a]之间的整数
F = randi([-5,5],10,1)	生成[-5,5]范围内的10*1的整数矩阵

 

 

矩阵大小

d = size(A)	d=x y   x是A的行数，y是A的列数 。三维数组也适合
[m,n] = size(A)	m是A的行数，n是A的列数
d = length(A)	返回矩阵A维度最大的维度数
d = numel(A)	返回矩阵中元素的总个数，行数 * 列数

 

 

 

矩阵的索引与访问

@注意： 下标从1开始

 

A(m,n)	访问A的m行n列
A(m)	访问A的某个元素，按列
A(m:n)	访问A的m~n的数据块，按列
A(m:a:n)	在m~n的范围内，每隔a个数访问，按列
A([a,b,c..])	直接访问第a,b,c ..个数据
A(a,:) / A(:,a)	a行所有数据 / a列所有数据
C = A([1,3],[4,2])	取第1行，第三行，第4列，第2列组合的矩阵 并且第4列为第一列
C= A(1:3:9,2:3:9)	取1,4,7行（1~9,每隔3），列也是如此
A(:,[a,b])	第a列和第b列的所有元素
A(a:b,[c,d])	a~b行和c列d列元素
A(find(B))	A和B是大小相同的矩阵，如果B的当前位置元素为非0，则取A中当前位置的元素
d = sub2ind(size(A),m,n)	d的值是A矩阵m行，n列对应的单下标索引
[m，n] = ind2sub(size(A),d)	A矩阵单下标d转换成双下标的m行,n列

矩阵的拼接与裁剪

矩阵拼接

C = cat(标识A,B)	A和B根据标识组合起来，得到新矩阵C 标识：1-各个矩阵竖着叠在一起（列数必须一样）            2-各个矩阵横着连在一起（行数必须一样）
C=vertcat（A,B）	两个矩阵竖着叠在一起，相当于cat标识为1的情况 。（列数必须一样）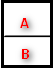
C = horzcat(A,B)	两个矩阵横着连在一起，相当于cat标识为2的情况 。（行数数必须一样）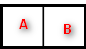
C=repmat(A,3,2)	矩阵A为一个块，以块为基本单位拼成3行个块，2列个块的新矩阵
C=blkdiag(A,B)	对角线拼接矩阵
C=kron(A,B)	红框行数和列数与A相同，每个红框里面的矩阵行数和列数与B相同，每个红框矩阵的元素是这个红框代表的元素（第一个红框是A中的0元素，第二个红框是A中的1元素....）*B中所有元素
索引扩展	以最小的代价把超过索引的点(矩阵外的一个点)包含进来	A =，A(2,4)=9, A=

，

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

矩阵裁剪

A(1:3,:)=[]

第1~3行所有列为空，也就是删除第1~3行

矩阵的运算与操作

矩阵算术运算

A'	矩阵转置	用函数transpose（A）也可以 用  .'  也是可以的 用ctranspose(A)也是可以的
inv(A)	A的逆矩阵
A*10	矩阵每个元素*10 ，同样适应于 + - * /
A+B 、A-B、 A*B 、A/B、 A\B	参考数学中两个矩阵的运算 A/B： A*inv(B) A\B：inv(A)*B
A.*B、A./B(A除以B)、A.\B(B除以A)	两个矩阵对应位置上的元素进行计算
A.^B、 A.^2、2.^A	对应位上元素进行计算
trace(A)	矩阵的迹，等于矩阵对角线元素的和，矩阵的特征值之和

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

矩阵翻转

flipud(A)	矩阵 上下翻转,默认中心轴为中间的那一行 共有偶数行的话直接翻转，奇数行的话中间一行不动
fliplr(A)	矩阵 左右翻转
rot90(A,k)	A按照逆时针旋转90*k度，k默认为1

 

 

reshape(A,a,b)	把A调整成a行，b列 。 A的大小始终为a*b， 单下标索引调整前后不能变