Andrew Ng机器学习课程笔记（五）之应用机器学习的建议

Andrew Ng机器学习课程笔记（五）之应用机器学习的建议

http://www.cnblogs.com/fydeblog/p/7368472.html

前言

学习了Andrew Ng课程，开始写了一些笔记，现在写完第5章了，先把这5章的内容放在博客中，后面的内容会陆续更新！

这篇博客主要记录了Andrew Ng课程第五章应用机器学习的建议，主要介绍了在测试新数据出现较大误差该怎么处理，这期间讲到了数据集的分类，偏差，方差，学习曲线等概念，帮助我们去理解结果，然后做出相应的措施。

1. 决定下一步怎么做

当我们运用训练好了的模型来预测未知数据的时候发现有较大的误差，我们下一步可以

做什么？有以下几种选择

①获得更多的训练实例——通常是有效的，但代价较大，下面的方法也可能有效，可考虑先采用下面的几种方法。

②尝试减少特征的数量

③尝试获得更多的特征

④尝试增加多项式特征

⑤尝试减少正则化程度λ

⑥尝试增加正则化程度λ

我们不应该随机选择上面的某种方法来改进我们的算法，而是运用一些机器学习诊断法来帮助我们知道上面哪些方法对我们的算法是有效的。

诊断法的意思是：这是一种测试法，你通过执行这种测试，能够深入了解某种算法到底是否有用。这通常也能够告诉你，要想改进一种算法的效果，什么样的尝试，才是有意义的。

2. 评估一个假设

说诊断法之前，先要说说怎样评估假设函数，此基础上讨论如何避免过拟合和欠拟合的问题。

通常数据是将数据集分成训练集和测试集，通常用70%的数据作为训练集，用剩下30%的数据作为测试集。

很重要的一点是训练集和测试集均要含有各种类型的数据，通常我们要对数据进行洗牌，然后再分成训练集和测试集。

测试集评估在通过训练集让我们的模型学习得出其参数后，对测试集运用该模型，我们有两种方式计算误差

①对于线性回归模型，我们利用测试集数据计算代价函数J

②对于逻辑回归模型，我们除了可以利用测试数据集来计算代价函数外，还可以计算误分类比，对于每一个测试集实例，按以下计算公式计算，然后对计算结果求平均。

3. 模型选择和交叉验证集

假设我们要在10个不同次数的二项式模型之间进行选择：

这时候需要使用交叉验证集来帮助选择模型。

数据集划分：使用60%的数据作为训练集，使用 20%的数据作为交叉验证集，使用 20%的数据作为测试集（6:2:2）

具体步骤：

①使用训练集训练出10个模型

②用10个模型分别对交叉验证集计算得出交叉验证误差（代价函数的值）

③选取代价函数值最小的模型

④用步骤3中选出的模型对测试集计算得出推广误差（
代价函数的值）

4. 诊断偏差和方差

高偏差和高方差的问题基本上来说是欠拟合和过拟合的问题。以下图为例

我们通常会通过将训练集和交叉验证集的代价函数误差与多项式的次数绘制在同一张图表上来帮助分析：

对于训练集，当d较小时，模型拟合程度更低，误差较大；随着d的增长，拟合程度提高，误差减小。

对于交叉验证集，当d较小时，模型拟合程度低，误差较大；但是随着d的增长，误差呈现先减小后增大的趋势，转折点是我们的模型开始过拟合训练数据集的时候。

我们如何判断是方差还是偏差呢？如下图所示

训练集误差和交叉验证集误差近似时：偏差/欠拟合

交叉验证集误差远大于训练集误差时：方差/过拟合

5. 正则化和偏差/方差

在我们在训练模型的过程中，一般会使用一些正则化方法来防止过拟合。但是我们可能会正则化的程度太高或太小了，即我们在选择λ的值时也需要思考与刚才选择多项式模型次数类似的问题。

我们选择一系列的想要测试的λ值，通常是 0-10 之间的呈现2倍关系的值（如：0,0.01,0.02,0.04,0.08,0.15,0.32,0.64,1.28,2.56,5.12,10 共12个）。我们同样把数据分为训练集、交叉验证集和测试集。

选择λ的方法为：

①使用训练集训练出12个不同程度正则化的模型

②用12模型分别对交叉验证集计算的出交叉验证误差

③选择得出交叉验证误差最小的模型

④运用步骤3中选出模型对测试集计算得出推广误差，我们也可以同时将训练集和交叉验证集模型的代价函数误差与λ的值绘制在一张图表上

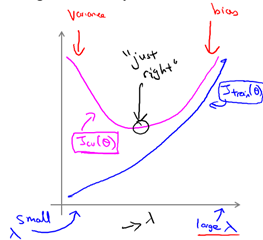
当λ较小时，训练集误差较小（过拟合）而交叉验证集误差较大

随着λ的增加，训练集误差不断增加（欠拟合），而交叉验证集误差则是先减小后增加

6. 学习曲线

学习曲线是一种很好的工具，使用学习曲线来判断某一个学习算法是否处于偏差、方差问题。

学习曲线是将训练集误差和交叉验证集误差作为训练集实例数量（m）的函数绘制的图表。

高偏差，增加数据到训练集不一定能有帮助，学习曲线趋于某一个错误不变。

高方差时，增加更多数据到训练集可能可以提高算法效果。

7. 决定下一步做什么（续）

经过上面几小节的内容，我们可以回答第一小节的6个方法了

①获得更多的训练实例——解决高方差

②尝试减少特征的数量——解决高方差

③尝试获得更多的特征——解决高偏差

④尝试增加多项式特征——解决高偏差

⑤尝试减少正则化程度λ——解决高偏差

⑥尝试增加正则化程度λ——解决高方差