BZOJ 4176 Lucas的数论 莫比乌斯反演+杜教筛

题意概述：求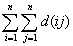，n<=10^9，其中d(n)表示n的约数个数。

分析：

　　首先想要快速计算上面的柿子就要先把d(ij)表示出来，有个神奇的结论：

　　

　　证明：当且仅当a,b没有相同的质因数的时候我们统计其贡献，可以发现所有被统计的(a,b)乘积的质因数分解形式正好和i,j的所有因数的质因数分解形式一一对应，不重不漏（对于b中质因数指数不为0对应的就是i中指数+b中指数的情况，对于b中质因数指数为0的情况对应i中指数的情况）。

　　然后就有如下的推导：

　　

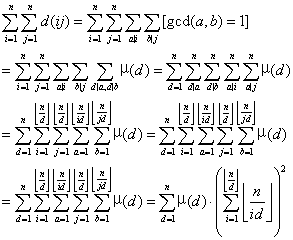
　　对于这个式子，整个数字分段来算，n/d一共sqrt(n)种取值，用杜教筛求μ的前缀和，后面那部分每次可以用sqrt(n/d)的复杂度计算出来，整个时间复杂度大约是O(n^(3/4))。（实在是太玄学了这个时间复杂度我不是很会算ORZ）

　　至于杜教筛......这里我就不讲了吧，看dalao链接！：http://jiruyi910387714.is-programmer.com/posts/195270.html

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<algorithm>
 #include<cmath>
 #include<queue>
 #include<set>
 #include<map>
 #include<vector>
 #include<cctype>
 using namespace std;
 const int mo=;
 const int maxn=;

 int N,pri[maxn],mu[maxn],tot;
 bool ntp[maxn];
 struct Hash{
     static const int sz=;
     static const int maxn=;
     int first[sz],np,next[maxn],id[maxn],val[maxn];
     Hash(){
         np=;
         memset(first,,sizeof(first));
     }
     void ins(int pos,int v){
         int i=pos%sz;
         next[++np]=first[i],first[i]=np;
         id[np]=pos,val[np]=v;
     }
     int query(int pos){
         int i=pos%sz;
         for(int p=first[i];p;p=next[p])
             if(id[p]==pos) return val[p];
         return -;
     }
 }hash;

 void get_mu()
 {
     ntp[]=ntp[]=,mu[]=;
     for(int i=;i<=;i++){
         if(!ntp[i]) pri[++tot]=i,mu[i]=-;
         for(int j=;j<=tot&&1ll*pri[j]*i<=;j++){
             ntp[i*pri[j]]=;
             if(i%pri[j]==){ mu[pri[j]*i]=; break; }
             mu[pri[j]*i]=-mu[i];
         }
     }
 }
 int F(int n){
     int re=;
     for(int i=,last;i<=n;i=last+)
         last=n/(n/i),re=(re+1ll*(last-i+)*(n/i)%mo)%mo;
     return re;
 }
 int S(int n){
     int re=hash.query(n);
     if(re!=-) return re;
     re=;
     for(int i=,last;i<=n;i=last+){
         last=n/(n/i);
         re=(re-1ll*(last-i+)*S(n/i)%mo+mo)%mo;
     }
     hash.ins(n,re);
     return re;
 }
 int solve(int n)
 {
     int re=,f;
     for(int i=,last;i<=n;i=last+){
         last=n/(n/i),f=F(n/i);
         re=(re+1ll*f*f%mo*(S(last)-S(i-)+mo)%mo)%mo;
     }
     return re;
 }
 int main()
 {
     get_mu();
     int sum=;
     for(int i=;i<=;i++)
         hash.ins(i,sum=(sum+mu[i]+mo)%mo);
     scanf("%d",&N);
     printf("%d\n",solve(N));
     return ;
 }