HDU5643-King's Game

BestCoder上的题，直接贴网站上的题目和题解了。很棒的题。

问题描述
为了铭记历史，国王准备在阅兵的间隙玩约瑟夫游戏。它召来了 n(1≤n≤5000) 个士兵，逆时针围成一个圈，依次标号 1,2,3...n。
第一轮第一个人从 1 开始报数，报到 1 就停止且报到 1 的这个人出局。
第二轮从上一轮出局的人的下一个人开始从 1 报数，报到 2 就停止且报到 2 的这个人出局。
第三轮从上一轮出局的人的下一个人开始从 1 报数，报到 3 就停止且报到 3 的这个人出局。
第 n-1 轮从上一轮出局的人的下一个人开始从 1 报数，报到 n-1 就停止且报到 n-1 的这个人出局。
最后剩余的人是幸存者，请问这个人的标号是多少？
输入描述
第一行一个整数表示测试组数：T(0<T≤5000) 。
每组数据占一行，包含一个整数 n，表示 n 个人围成一圈。
输出描述
共 T 行。对每组数据，输出幸存者的编号。
输入样例
2
2
3
输出样例
2
2
Hint
对于第一组数据，一开始报到 1 的人即标号为 1 的人退出，幸存者是 2 号。
对于第二组数据，一开始报到 1 的人即标号 1 的人退出。接着 2 号报 1，3 号报 2，报到 2 的人即 3 号退出。幸存者是 2 号。

题解：

约瑟夫问题的一个变种，然而题目全部是在唬人，就是一个简单的递推。虽然我知道有人会打表。。。
我们看看裸的约瑟夫是怎么玩的：n 个人，每隔 k 个删除。
由于我们只关心最后一个被删除的人，并不关心最后的过程，所以，我们没有必要也不能够模拟整个过程。我们用递推解决。假设有n个人围成环，标号为[0,n-1]从0开始的好处是取模方便），每数k个人杀一个的情况下，最后一个存活的人的编号是f[n]。
我们有f[1]=0,这不需要解释。
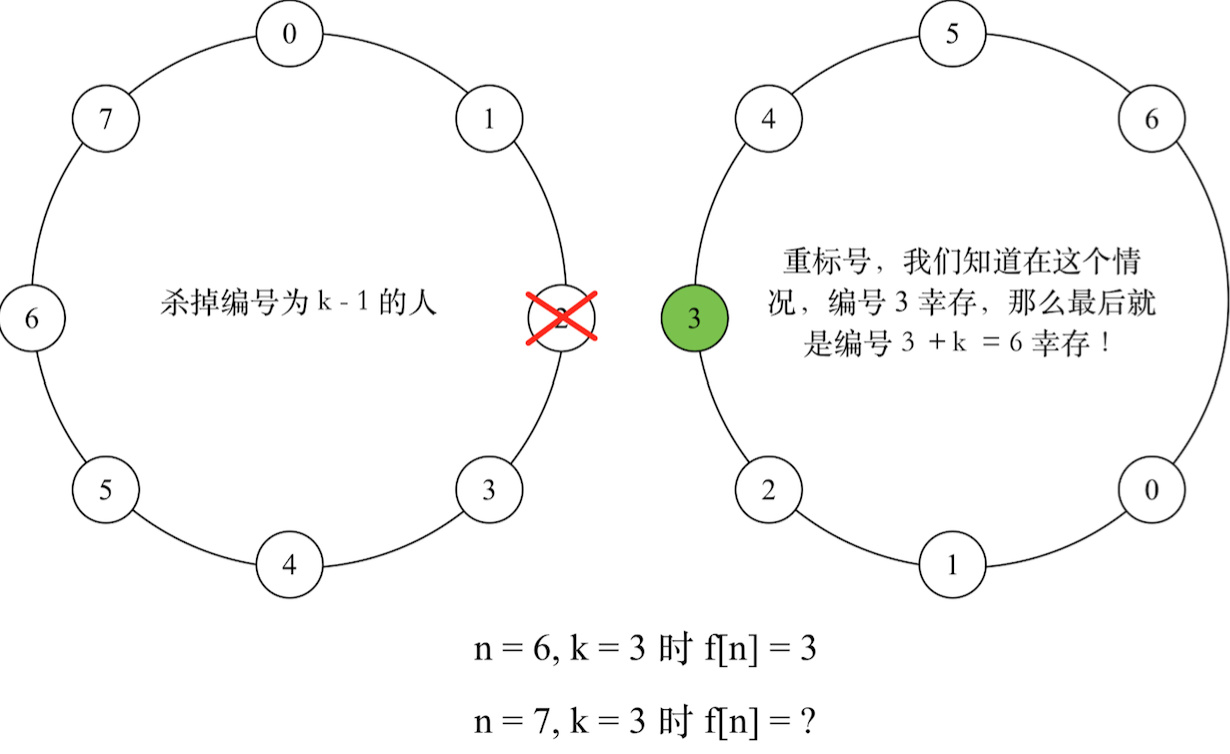
接着考虑一般情况f[n],第一个杀死的人的编号是k-1,杀死后只剩下n-1个人了，那么我们重新编号！
原来编号为k的现在是0号，也就是编号之间相差3我们只要知道现在n-1个人的情况最后是谁幸存也就知道n个人的情况是谁幸存。幸运的是f[n-1]已经算出来了那f[n]就是在f[n-1]的基础上加上一个k即可不要忘记总是要取模。

所以递推式子是： f[i]={ 0 i=1   (f[i - 1] + k) mod i other
此题只用在原版约瑟夫问题上加一维，由于依次隔 1,2,3...n-1个人删除，所以用 f[i][j]表示 i个人，依次隔 j,j+1...j+i-1 个人的幸存者标号。
根据刚才的重标号法，第一次 j-1 号出局，从 j 开始新的一轮，从 j+1 开始清除，剩余 i-1 个人，也有递推式子：
f[i][j]={ 0  i=1 (f[i - 1][j+1] + j) mod i other
答案就是 f[n][1]+1（将标号转移到 [1,n]），问题轻松解决。
复杂度：预处理 O(n^2)，查询 O(1)，总复杂度 O(n^2)。由于可以滚动数组以及常数太小，所以 n 给了 5000。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;

const int N = 5010;

int f[2][N]; // f[i][j]表示i个人 依次隔j,j+1...j+i−1个人删除的幸存者标号
// f[i][j]=(f[i-1][j+1]+j)%i
int ans[N];

int main()
{
    f[0][0] = 0;
    for (int i = 0; i < 5000; ++i)
        f[1][i] = 0;   // 1个人的时候幸存者永远是0
    for (int i = 1; i <= 5000; ++i) {
        for (int j = 1; j <= 5000; ++j) {
            f[i%2][j] = (f[(i - 1)%2][j + 1] + j) % i;
        }
        ans[i] = f[i%2][1];
    }
    int t;
    scanf("%d", &t);
    while (t--) {
        int n;
        scanf("%d", &n);
        printf("%d\n", ans[n] + 1);
    }
    return 0;
}