【Ural1057】幂和的数量

【题目描述】

写一个程序来计算区间[X,Y]内满足如下条件的整数个数：它恰好等于K个互不相等的B的整数幂之和。

举个例子。令X=15，Y=20，K=2，B=2。在这个例子中，区间[15,20]内有3个整数恰好等于两个互不相等的2的整数幂之和：

17=2^4+2^0

18=2^4+2^1

20=2^4+2^2

【输入格式】

输入文件的第一行有两个空格隔开的整数X,Y（1<=X<=Y<=2^31-1）.

第二行有两个整数K,B（1<=K<=20,2<=B<=10）.

【输出格式】

输出一行一个整数，即[X,Y]中恰好等于K个互不相等的B的整数幂之和的数的个数。

【分析】

数位类统计，上一张图：

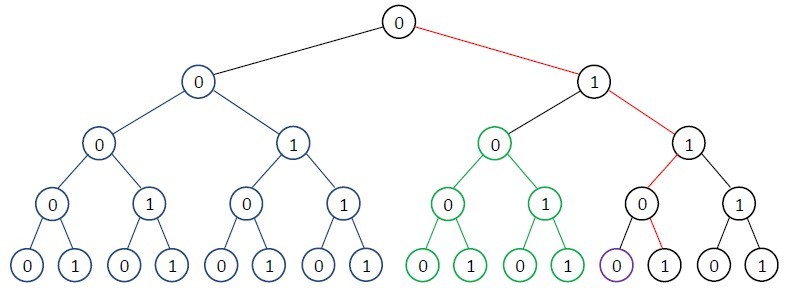
用f[i][j]来表示高度为i的二叉树下进制位有j个为1的数的个数。

对于询问n，我们需要求出不超过n的最大B进制表示只含0、1的数：
找到n 的左起第一位非0、1 的数位，将它变为1，并将右面所有数位设为1。（因为大于1的肯定不可取，后面置为1使它最接近原来的数）
将得到的B进制表示视为二进制进行询问即可。

 #include <cstdio>
 #include <iostream>
 #include <cstring>
 int f[][];
 int x,y,k,b;

 int work(int x,int k);
 int change(int x);
 int main()
 {
     int i,j;
     //初始化
     f[][]=;
     for(i=;i<=;i++)
     {
         f[i][]=f[i-][];
         for(j=;j<=i;j++)
         f[i][j]=f[i-][j]+f[i-][j-];
     }
     scanf("%d%d%d%d",&x,&y,&k,&b);
     printf("%d\n",work(change(y),k)-work(change(x-),k));
     return ;
 }
 int change(int x)
 {
     int p=,tot=;
     while(x>=(long long)p*b) p*=b,++tot;//用来统计有tot个b进制位
     int ans=;
     //b进制转2进制
     while(p && x/p<=)
     {
           ans+=x/p*(<<tot);
           tot--;
           x%=p;
           p/=b;
     }
     ans+=(<<(tot+))-;
     return ans;
 }
 //统计[0..x]内二进制表示含k个1的数的个数
 int work(int x,int k)
 {
     //tot记录当前路径上已有的1的数量
     int ans=,tot=;
     for(int i=;i;i--)
     {
         if(x&(<<i))
         {
             ++tot;
             //跳出
             if(tot>k)break;
             x^=(<<i);
         }
         if((<<(i-))<=x)
         ans+=f[i-][k-tot];
     }
     if(x+tot==k)++ans;
     return ans;
 }