POJ - 1942 D - Paths on a Grid

Imagine you are attending your math lesson at school. Once again, you are bored because your teacher tells things that you already mastered years ago (this time he's explaining that (a+b) ²=a ²+2ab+b ²). So you decide to waste your time with drawing modern art instead.

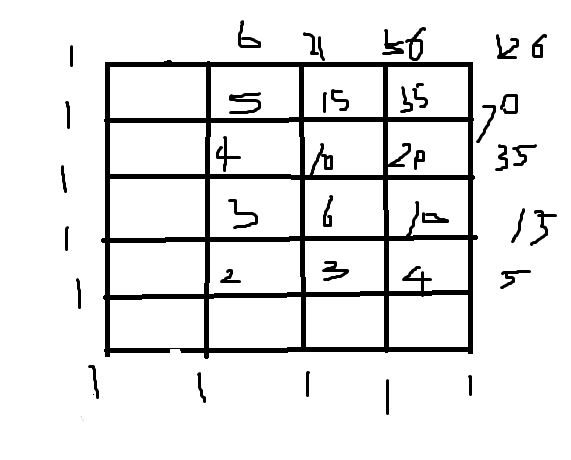
Fortunately you have a piece of squared paper and you choose a rectangle of size n*m on the paper. Let's call this rectangle together with the lines it contains a grid. Starting at the lower left corner of the grid, you move your pencil to the upper right corner, taking care that it stays on the lines and moves only to the right or up. The result is shown on the left: 

Really a masterpiece, isn't it? Repeating the procedure one more time, you arrive with the picture shown on the right. Now you wonder: how many different works of art can you produce?

Input

The input contains several testcases. Each is specified by two unsigned 32-bit integers n and m, denoting the size of the rectangle. As you can observe, the number of lines of the corresponding grid is one more in each dimension. Input is terminated by n=m=0.

Output

For each test case output on a line the number of different art works that can be generated using the procedure described above. That is, how many paths are there on a grid where each step of the path consists of moving one unit to the right or one unit up? You may safely assume that this number fits into a 32-bit unsigned integer.

Sample Input

5 4
1 1
0 0

Sample Output

126

2

题意：输入n，m，代表n*m的矩阵，求从左下角到右上角的方法有多少种

思路：用我们平常的加法原理可以得出这个答案，但是n，m范围是unsigned int我们不能开这么大的数组

我们可以发现其实我们肯定会走n+m步，其中n步向上，m步向右，我们走上，我们路线肯定是由

n个上，m个右组成，所以我们在这求出一个组合数C（n+m,m），代表从这个路线顺序里面挑出

m个位置为向右走，用C(n+m,n)也是一样的结果

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
using namespace std;
unsigned C(unsigned n,unsigned m)//n,m的每个地方都记得用unsigned类型
{
    if(m>n-m) m=n-m;
    unsigned t1,t2;
    t1=n;
    t2=m;
    double vis=1.0;
    while(t2>)//用double型存储组合数，可以每次进行约分，如果是实在是整型不好存储的话那就只能使用这个进行约分了
    {
        vis*=(double)(t1--)/(double)(t2--);
    }
    return (unsigned)(vis+0.5);//四舍五入
}
unsigned n,m;
int main()
{
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        if(!m && !n)
            break;
        cout<<C(n+m,n)<<endl;
    }
}