交叉熵的数学原理及应用——pytorch中的CrossEntropyLoss()函数

分类问题中，交叉熵函数是比较常用也是比较基础的损失函数，原来就是了解，但一直搞不懂他是怎么来的？为什么交叉熵能够表征真实样本标签和预测概率之间的差值？趁着这次学习把这些概念系统学习了一下。

首先说起交叉熵，脑子里就会出现这个东西：

随后我们脑子里可能还会出现Sigmoid()这个函数:

pytorch中的CrossEntropyLoss()函数实际就是先把输出结果进行sigmoid，随后再放到传统的交叉熵函数中，就会得到结果。

---

那我们就先从sigmoid开始说起，我们知道sigmoid的作用其实是把前一层的输入映射到0~1这个区间上，可以认为上一层某个样本的输入数据越大，就代表这个样本标签属于1的概率就越大，反之，上一层某样本的输入数据越小，这个样本标签属于0的概率就越大，而且通过sigmoid函数的图像我们可以看出来，随着输入数值的增大，其对概率增大的作用效果是逐渐减弱的，反之同理，这就是非线性映射的一个好处，让模型对处于中间范围的输入数据更敏感。下面是sigmoid函数图：

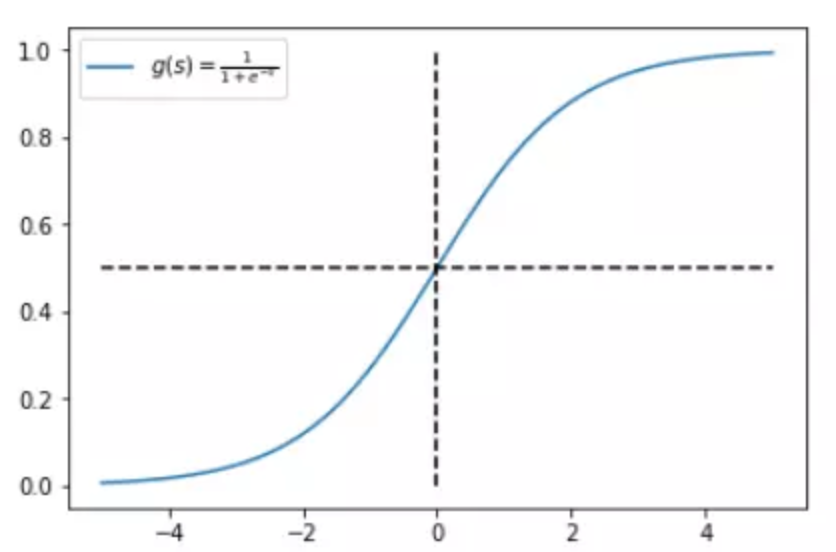
既然经过sigmoid之后的数据能表示样本所属某个标签的概率，那么举个例子，我们模型预测某个样本标签为1的概率是：

那么自然的，这个样本标签不为1的概率是：

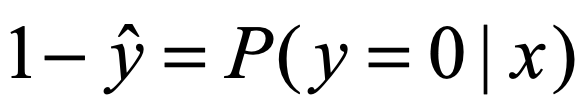
从极大似然的角度来说就是：

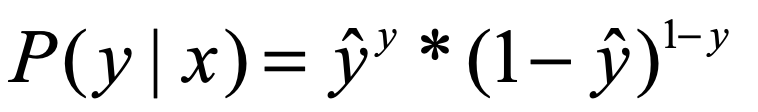
上式可以理解为，某一个样本x，我们通过模型预测出其属于样本标签为y的概率，因为y是我们给的正确结果，所以我们当然希望上式越大越好。

下一步我们要在  P( y | x )  的外面套上一层log函数，相当于进行了一次非线性的映射。log函数是不会改变单调性的，所以我们也希望  log( P( y | x ) )  越大越好。

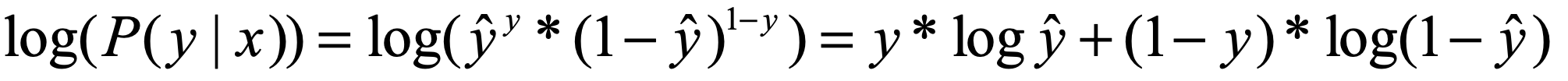
这样，就得到了我们一开始说的交叉熵的形式了，但是等一等，好像还差一个符号。

因为一般来说我们相用上述公式做loss函数来使用，所以我们想要loss越小越好，这样符合我们的直观理解，所以我们只要  -log( P( y | x ) )  就达到了我们的目的。

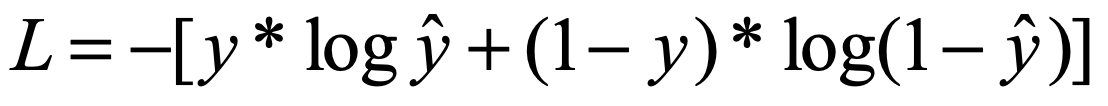
上面是二分类问题的交叉熵，如果是有多分类，就对每个标签类别下的可能概率分别求相应的负log对数然后求和就好了：

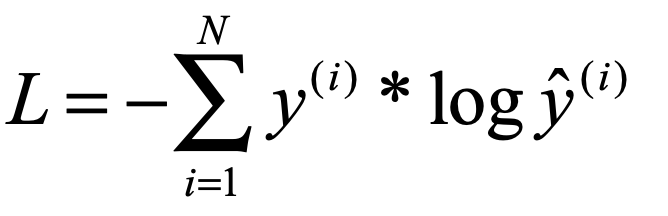
是不是突然也感觉有些理解了，(*^__^*) ……

---

上面是对交叉熵进行了推到，下面要结合pytorch中的函数 CrossEntropyLoss()  来说一说具体怎么使用了。

举个小例子，假设我们有个一样本，他经过我们的神经网络后会输出一个5维的向量，分别代表这个样本分别属于这5种标签的数值（注意此时我们的5个数求和还并不等于1，需要先经过softmax处理，下面会说），我们还会从数据集中得到该样本的正确分类结果，下面我们要把经过神经网络的5维向量和正确的分类结果放到CrossEntropyLoss() 中，看看会发生什么：

看一看我们的input和target： 　

可以看到我们的target就是一个只有一个数的数组形式（不是向量，不是矩阵，只是一个简单的数组，而且里面就一个数），input是一个5维的向量，但这，在计算交叉熵之前，我们需要先获得下面交叉熵公式的。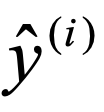

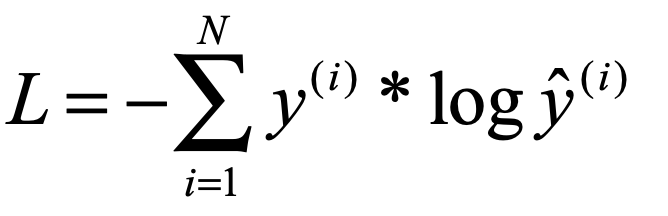
此处的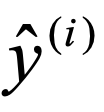需要我们将输入的input向量进行softmax处理，softmax我就不多说了，应该比较简单，也是一种映射，使得input变成对应属于每个标签的概率值，对每个input[i]进行如下处理：

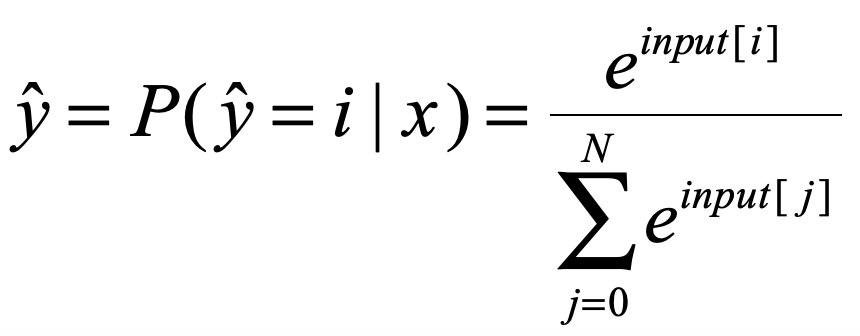
这样我们就得到了交叉熵公式中的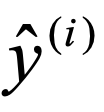

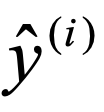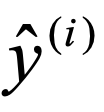随后我们就可以把带入公式了，下面我们还缺就可以了，而奇怪的是我们输入的target是一个只有一个数的数组啊，而是一个5维的向量，这什么情况？

原来CrossEntropyLoss() 会把target变成ont-hot形式（网上别人说的，想等有时间去看看函数的源代码随后补充一下这里），我们现在例子的样本标签是【4】（从0开始计算）。那么转换成one-hot编码就是【0，0，0，0，1】，所以我们的最后也会变成一个5维的向量的向量，并且不是该样本标签的数值为0，这样我们在计算交叉熵的时候只计算给定的那一项的sorce就好了，所以我们的公式最后变成了：

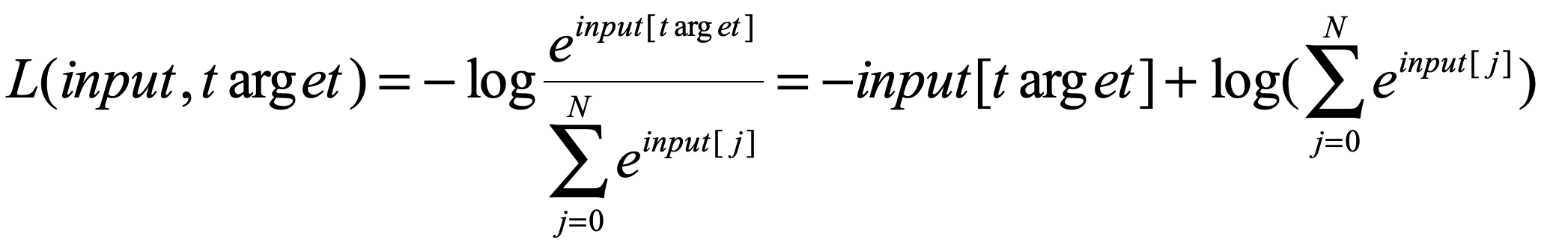
好，安装上面我们的推导来运行一下程序：

破发科特~~~~~~

圣诞节快乐(*^__^*) ……