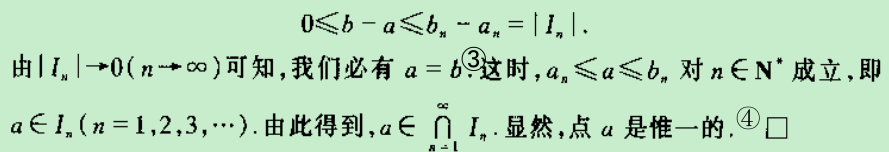
①

②这里用到了极限与不等关系

③如果a≠b，那么便不会有$\lim _{n\rightarrow \infty }\left| I_n \right| =0$

④如果还存在一点c在

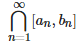
内，那么同样也不会有$\lim _{n\rightarrow \infty }\left| I_n \right| =0$

希望深入了解闭区间套定理（Nested intervals theorem），请看讲解2：http://www.cnblogs.com/iMath/p/6260953.html

闭区间套定理（Nested intervals theorem）讲解1的更多相关文章

  1. 闭区间套定理（Nested intervals theorem）讲解2

    ①确界与极限,看完这篇你才能明白 http://www.cnblogs.com/iMath/p/6265001.html ②这个批注由这个问题而来 表示$c$可能在$\bigcap_{n=1}^{\i ...

  2. 闭区间套定理（Nested intervals theorem）

    ① ②这里用到了极限与不等关系 ③如果a≠b,那么便不会有$\lim _{n\rightarrow \infty }\left| I_n \right| =0$ ④如果还存在一点c在内,那么同样也不会 ...

  3. 华东师范大学p163页，用闭区间套定理证明数列的可惜收敛准则，被网友解决了。

  4. 主定理（Master Theorem）与时间复杂度

    1. 问题 Karatsuba 大整数的快速乘积算法的运行时间(时间复杂度的递推关系式)为 T(n)=O(n)+4⋅T(n/2),求其最终的时间复杂度. 2. 主定理的内容 3. 分析 所以根据主定理 ...

  5. [笔记] 兰道定理 Landau's Theorem

    兰道定理的内容: 一个竞赛图强连通的充要条件是:把它的所有顶点按照入度d从小到大排序,对于任意\(k\in [0,n-1]\)都不满足\(\sum_{i=0}^k d_i=\binom{k+1}{2} ...

  6. 斯托克斯定理（Stokes' theorem）

    1. 几种形式 ∮∂SPdx+Qdy+Rdz=∬S∣∣∣∣∣∣cosα∂∂xPcosβ∂∂yQcosγ∂∂zR∣∣∣∣∣∣dS ∮∂Ωw=∬Ωdw 左边是内积: 右边是外积: 物理上的应用: ∮∂SE ...

  7. 无限二等分[0,1]这个区间之后还剩下啥？what's left after dividing an unit interval [0,1] infinitely many times?

    Dividing an unit interval \([0,1]\) into two equal subintervals by the midpoint \(\dfrac {0+1} {2}=\ ...

  8. 从一个点的长度是多少说起（Talking started from the length of a point on the real number line）

    From the perspective of analytical geometry, an interval is composed of infinitely many points, whil ...

  9. 深入理解无穷级数和的定义（the sum of the series）

    Given an infinite sequence (a1, a2, a3, ...), a series is informally the form of adding all those te ...

随机推荐

  1. 永久关闭selinux

    selinux这东西,有时候真让人搞不懂. 临时关闭: setenforce 0 getenforce #查看状态是否是disabled 永久关闭: vim /etc/sysconfig/selinu ...

  2. 赋值文件夹名称为日期的doc命令

    copy D:\111.txt d:\%date:~0,4%年%date:~5,2%月%date:~8,2%日.*

  3. Redis高可用详解：持久化技术及方案选择

    文章摘自:https://www.cnblogs.com/kismetv/p/9137897.html 前言 在上一篇文章中,介绍了Redis的内存模型,从这篇文章开始,将依次介绍Redis高可用相关 ...

  4. css table样式

    1.table样式首先设置表格边框,属性设置表格的边框是否被合并为一个单一的边框. table{ border-collapse: collapse; border-spacing: 0;} 2.固定 ...

  5. 当 Visual Studio 扩展遇到错误时

    我是遇到了 Github 扩展经常在 Visual Studio 启动时报错,找了一下可以尝试以下方法: 首先卸载插件 然后删除 %LocalAppData%\Microsoft\VisualStud ...

  6. react-无状态组件

    import React, { Component } from "react"; //import PostItem from "./PostItem"; / ...

  7. flutter 环境安装以及配置

    首先需要下载flutter源码,以下是github地址: https://github.com/flutter/flutter 然后需要安装git环境吧,下图红框可以自行下载安装 接下来需要安装flu ...

  8. KVM上如何让虚拟机支持虚拟化(kvm虚拟化的嵌套)

    http://blog.csdn.net/swimming_in_it_/article/details/53320141http://blog.csdn.net/wickedglory/articl ...

  9. tar加密

    # tar -czvf - file_name|openssl des3 -salt -k |dd of=file_name.des3 # ls flie_name file_name.des3 # ...

  10. 菜鸟教程之工具使用（六）——让Maven项目直接在eclipse内部的Tomcat中运行

    Hello,大家好,好久不见!最近终于安定下来了,可以静下心来写东西了.先写篇简单的,找找感觉.工具系列的本身就比较简单,没什么技术含量.因为说到底,工具只是辅助我们工作的,知道怎么用,然后剩下的就是 ...