[UE4]运行时脱离视角,进入自由视角

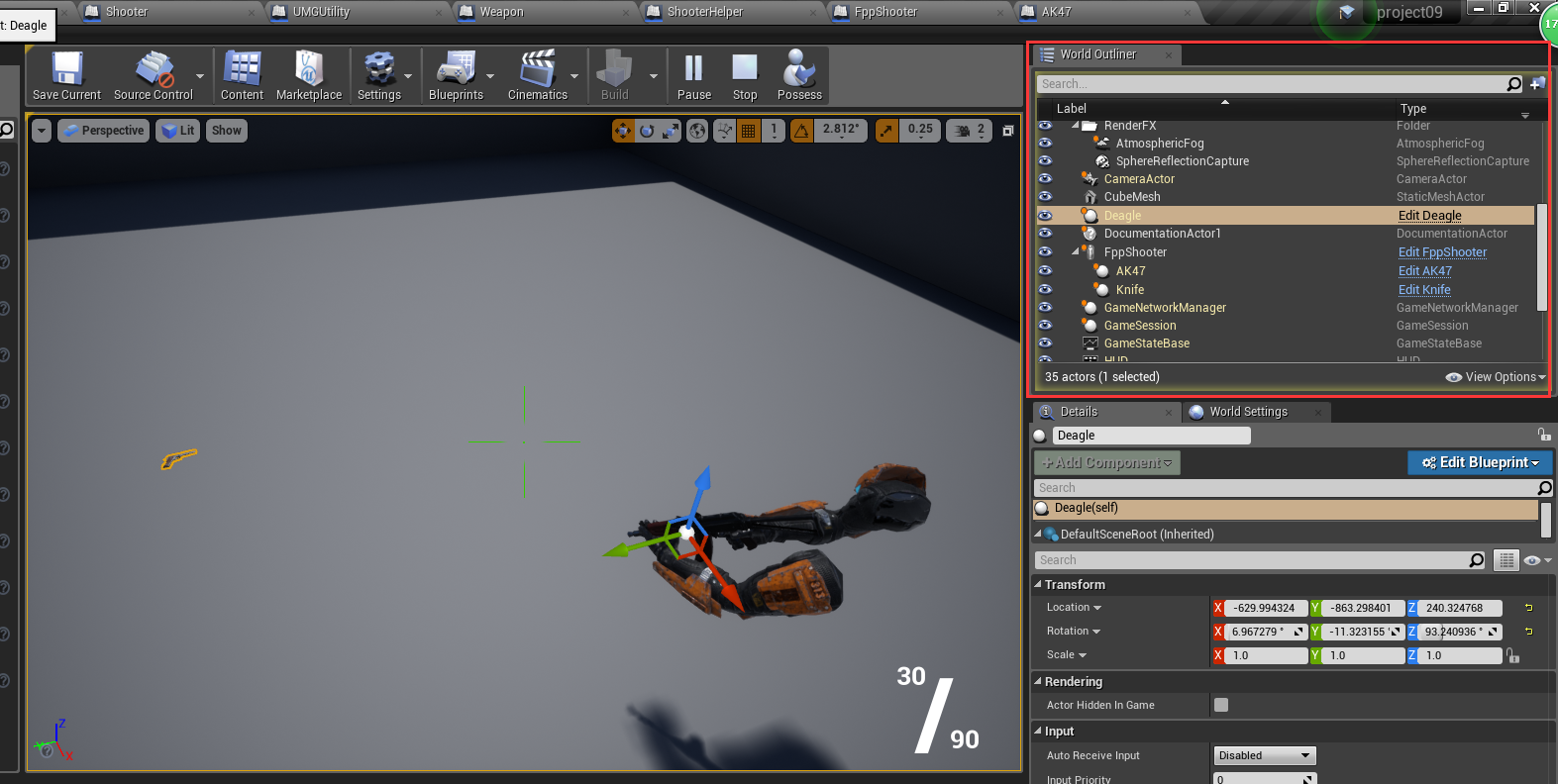
按 Shift + F1让鼠标脱离游戏窗口,然后点击右上角的 按钮,然后鼠标在游戏窗口点击一下,就只有自由漫游了。
按钮,然后鼠标在游戏窗口点击一下,就只有自由漫游了。
还可以点击选中Word Outliner窗口的物体。
[UE4]运行时脱离视角,进入自由视角的更多相关文章
- [UE4]运行时进入观察模式
- [UE4]运行时创建Actor
- Xwork概况 XWork是一个标准的Command模式实现,并且完全从web层脱离出来。Xwork提供了很多核心功能:前端拦截机(interceptor),运行时表单属性验证,类型转换,强大的表达式语言(OGNL – the Object Graph NavigationLanguage),IoC(Inversion of Control反转控制)容器等。 ----------------
Xwork概况 XWork是一个标准的Command模式实现,并且完全从web层脱离出来.Xwork提供了很多核心功能:前端拦截机(interceptor),运行时表单属性验证,类型转换,强大的表达式 ...
- 在Amazon FreeRTOS V10中使用运行时统计信息
在MCU on Eclipse网站上看到Erich Styger在8月2日发的博文,一篇关于在Amazon FreeRTOS V10中使用运行时统计信息的文章,本人觉得很有启发,特将其翻译过来以备参考 ...
- 《深入理解Java虚拟机》(二)Java虚拟机运行时数据区
Java虚拟机运行时数据区 详解 2.1 概述 本文参考的是周志明的 <深入理解Java虚拟机>第二章 ,为了整理思路,简单记录一下,方便后期查阅. 2.2 运行时数据区域 Java虚拟机 ...
- JVM 专题十二:运行时数据区(七)对象的实例化内存布局与访问定位
1. 对象的实例化 1.1 创建对象的方式 new 最常见的方式 变形1 : Xxx的静态方法 变形2 : XxBuilder/XxoxFactory的静态方法 Class的newInstance() ...
- JVM运行时数据区--纵向补充--对象的实例化内存布局与访问定位
对象的实例化 创建对象的方式 1.new:最常见的方式(本质是构造器) 变形1 : Xxx的静态方法 变形2 : XxBuilder/XxoxFactory的静态方法 2.Class的newInsta ...
- linux下实现在程序运行时的函数替换(热补丁)
声明:以下的代码成果,是参考了网上的injso技术,在本文的最后会给出地址,同时非常感谢injso技术原作者的分享. 但是injso文章中的代码存在一些问题,所以后面出现的代码是经过作者修改和检测的. ...
- 探究JVM——运行时数据区
最近在读<深入理解Java虚拟机>,收获颇丰,记录一下,部分内容摘自原书. Java虚拟机在执行Java程序的过程中会把它所管理的内存划分为若干个不同的数据区域.这些区域都有各自的用途,以 ...
随机推荐
- Go Example--方法
package main import "fmt" //定义结构体 type rect struct { width,height int } //定义结构体指针的方法 func ...
- 【HAOI2015】 T1
为什么感觉越来越迷了X. X 原题: 有一棵点数为 N 的树,树边有边权.给你一个在 0~N 之内的正整数 K,你要在这棵树中选择 K 个点,将其染成黑色,并将其他的N-K 个点染成白色.将所有点染色 ...
- LG4781 【模板】拉格朗日插值
题意 题目描述 由小学知识可知,$n$个点$(x_i,y_i)$可以唯一地确定一个多项式 现在,给定$n$个点,请你确定这个多项式,并将$k$代入求值 求出的值对$998244353$取模 输入输出格 ...
- vue全家桶+Koa2开发笔记(4)--redis
redis用来在服务器端存放session 1 安装redis brew install redis 启动redis redis-server 2 安装两个中间件 npm i koa-ge ...
- HTTP与TCP的区别和联系--转载
相信不少初学手机联网开发的朋友都想知道Http与Socket连接究竟有什么区别,希望通过自己的浅显理解能对初学者有所帮助. 一.基本概念 1.TCP连接 手机能够使用联网功能是因为手机底层实现了TCP ...
- 把oracle数据库恢复到某个时间点或者某个scn
alter session set nls_date_format='yyyymmdd hh24:mi:ss'; select sysdate from dual; conn dbauser/1234 ...
- hasura graphql-engine v1.0.0-alpha30 功能试用
hasura graphql-engine v1.0.0-alpha30 有好多新的功能的添加 环境准备 docker-compose 文件 version: '3.6' services: post ...
- WikiBooks/Cg Programming
https://en.wikibooks.org/wiki/Cg_Programming Basics Minimal Shader(about shaders, materials, and gam ...
- python, 用filter实现素数
# _*_ coding:utf-8 _*_ #step1: 生成一个序列def _odd_iter(): n = 1 while True: n = n + 1 yield n #Step2: 定义 ...
- webpack 相关插件及作用(表格)
webpack 相关插件及作用: table th:first-of-type { width: 200px; } table th:nth-of-type(2) { width: 140px; } ...
