回溯---N皇后

N 皇后

51. N-Queens (Hard)

题目描述：

  在n*n的矩阵中摆放n个皇后，并且每个皇后不能在同一列，同一个对角线上，求所有的n皇后解。

思路分析：

  一行一行地摆放，在确定一行中的那个皇后应该摆在哪一列时，需要用三个标记数组来确定某一列是否合法。这三个标记数组分别为：列标记数组，45度对角线标记数组和135度对角线标记数组。

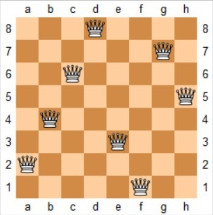
  45度对角线标记数组的长度为2*n-1，通过下图可以明确（r,c）的位置所在的数组下标为（r+c）

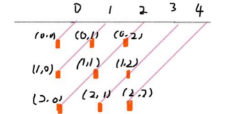
  135 度对角线标记数组的长度也是 2 * n - 1，(r, c) 的位置所在的数组下标为 n - 1 - (r - c)。

代码：

class Solution {
public boolean []colUsed;
public boolean[]flag45Used;
public boolean[]flag135Used;
public char[][]nQueens; //矩阵
public List<List<String>>solveNQueens(int n){
    List<List<String>>res=new ArrayList<>();
    nQueens=new char[n][n];
    for(int i=0;i<n;i++){ //初始化矩阵
        for(int j=0;j<n;j++){
            nQueens[i][j]='.';
        }
    }
    colUsed=new boolean[n];
    flag45Used=new boolean[2*n-1];
    flag135Used=new boolean[2*n-1];
    backtracking(0,res,n);
    return res;
}
public void backtracking(int row,List<List<String>>res,int n){
    if(row==n){    //row==n表示已经将n个皇后放好，所以为一种结果
        List<String>list=new ArrayList<>(); //保存一种结果
        for(char[]chars:nQueens){
            list.add(new String(chars));
        }
        res.add(list);
        return ;
    }
    for(int col=0;col<n;col++){
        int flag45Index=row+col ;//（row，col）对应在45度标记数组中的位置。
        int flag135Index=n-1-(row-col) ;//（row，col）对应在135度标记数组中的位置。
        if(colUsed[col]||flag45Used[flag45Index]||flag135Used[flag135Index]) //该列或者该对角线已经有皇后
            continue;
        nQueens[row][col]='Q'; //该位置放皇后
        colUsed[col]=true;
        flag45Used[flag45Index]=true;
        flag135Used[flag135Index]=true;
        backtracking(row+1,res,n);//进行下一行皇后放置
        nQueens[row][col]='.'; //该位置还原，回溯
        colUsed[col]=false;
        flag45Used[flag45Index]=false;
        flag135Used[flag135Index]=false;
    }
}
}