Java 实现《编译原理》中间代码生成 -逆波兰式生成与计算 - 程序解析

Java 实现《编译原理》中间代码生成 -逆波兰式生成与计算 - 程序解析

编译原理学习笔记

（一）逆波兰式是什么？

逆波兰式（Reverse Polish notation，RPN，或逆波兰记法），也叫 后缀表达式（将运算符写在操作数之后）

一般的表达式又称 中缀表达式，这种表达式的二元运算符放在两个运算量 之间。而逆波兰表达式又称 后缀表达式，这种表达式把运算符放在运算量 后面。

比如如 a+b 的逆波兰式表示为 ab+

注意：逆波兰式是一个无括号表达式；逆波兰式的运算符出现的顺序就是原表达式的运算顺序。

（二）逆波兰式编译原理有什么关系？

逆波兰式，三元式，四元式等是编译原理 - 中间代码生成阶段的常见的中间代码形式。

（三）本篇任务

通过设计，使用 Java 语言编写一个逆波兰式生成程序，测试效果：

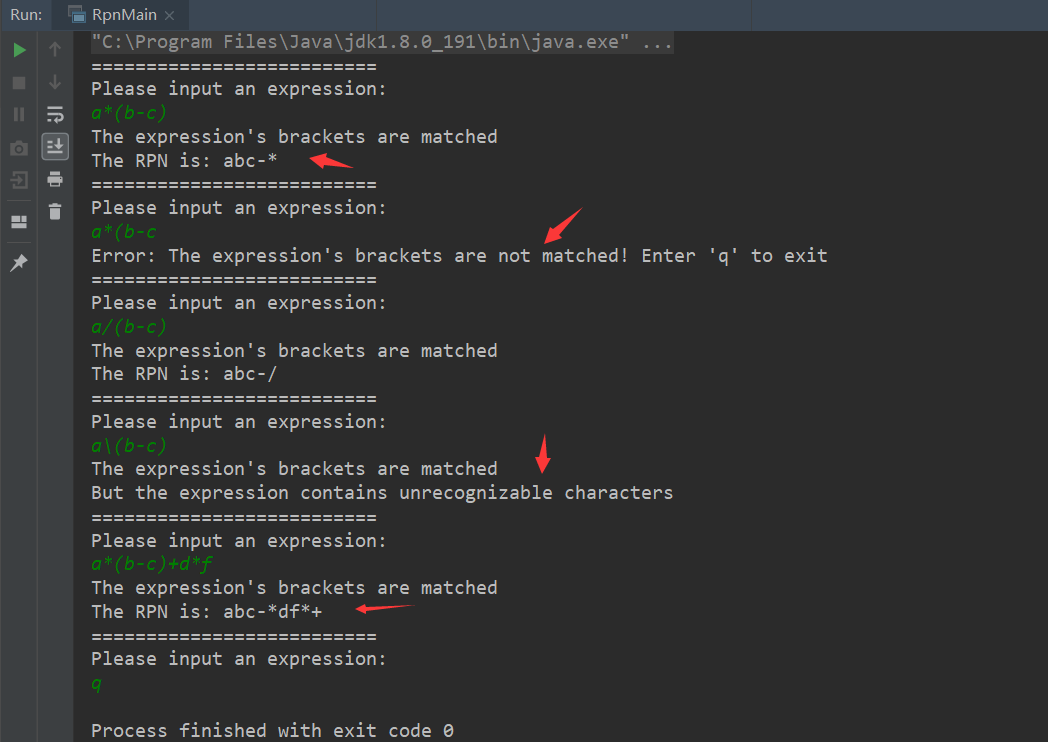
（四）Java 源代码

package com.java997.analyzer.rpn;

import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;
import java.util.Stack;

/**
 * <p>
 * 逆波兰式
 *
 * @author XiaoPengwei
 * @since 2019-06-19
 */
public class RpnMain {

    /**
     * 检查算术表达术括号是否匹配, 语法是否正确
     *
     * @param s 算术表达术
     * @return boolean
     */
    public boolean isMatch(String s) {

        //括号符号栈
        Stack<Character> charStack = new Stack<>();

        //将表达式的字符串转换成数组
        char[] charArray = s.toCharArray();

        //遍历数组
        for (char aChar : charArray) {
            if (aChar == '(') {
                charStack.push(aChar);
            } else if (aChar == ')') {
                //如果是 ) , 且栈为空则返回 false
                if (charStack.isEmpty()) {
                    return false;
                } else {
                    //如果是 ) , 且栈不为空则返回 false
                    //peek() 是返回栈顶的值, 不做其他操作
                    if (charStack.peek() == '(') {
                        //把栈顶的值删除
                        charStack.pop();
                    }
                }
            }
        }
        //走到这里, 栈为空则表达式正确
        return charStack.empty();
    }

    /**
     * 判断是否为操作符 + - * /
     *
     * @param charAt
     * @return boolean
     */
    public boolean isOperator(char charAt) {
        return charAt == '+' || charAt == '-' || charAt == '*' || charAt == '/';
    }

    /**
     * 根据正确的表达式, 获取逆波兰式
     *
     * @param input
     * @return java.lang.String
     */
    public StringBuilder getRpn(String input) {
        //结果
        StringBuilder sb = new StringBuilder();
        sb.append("The RPN is: ");
        //运算符栈
        Stack<Character> opStack = new Stack();

        //运算符优先级
        Map<Character, Integer> opMap = new HashMap(5);
        opMap.put('(', 0);
        opMap.put('+', 1);
        opMap.put('-', 1);
        opMap.put('*', 2);
        opMap.put('/', 2);

        //处理字符串
        for (int i = 0; i < input.length(); i++) {
            //如果是'('直接压栈
            if (input.charAt(i) == '(') {
                opStack.push('(');
            } else if (new RpnMain().isOperator(input.charAt(i))) {
                //如果是运算符
                char curOp = input.charAt(i);
                //如果运算符栈是空，就直接压栈
                if (opStack.isEmpty()) {
                    opStack.push(curOp);
                } else if (opMap.get(curOp) > opMap.get(opStack.peek())) {
                    //运算符栈不为空，且当当前运算符的优先级比站内第一个运算符的优先级高的时候，压栈
                    opStack.push(curOp);
                } else {
                    //栈不为空，且运算符的优先级小于等于栈顶元素
                    for (int j = 0; j <= opStack.size(); j++) {
                        //弹出栈内第一个元素
                        char ch = opStack.pop();
                        sb.append(ch);
                        if (opStack.isEmpty()) {
                            opStack.push(curOp);
                            break;
                        } else if (opMap.get(curOp) > opMap.get(opStack.peek())) {
                            opStack.push(curOp);
                            break;
                        }
                    }
                }
            } else if (input.charAt(i) == ')') {
                //如果是')'就把站内'('上的元素都弹出栈
                for (int j = 0; j < opStack.size(); j++) {
                    char c = opStack.pop();
                    if (c == '(') {
                        break;
                    } else {
                        sb.append(c);
                    }
                }
            } else if ('A'<=input.charAt(i)&&input.charAt(i)<='Z'){
                //如果是字母就直接添加
                sb.append(input.charAt(i));
            }else if ('a'<=input.charAt(i)&&input.charAt(i)<='z'){
                //如果是字母就直接添加
                sb.append(input.charAt(i));
            }else if (Character.isDigit(input.charAt(i))){
                //如果是数字
                sb.append(input.charAt(i));
            }else {
                return new StringBuilder("But the expression contains unrecognizable characters");
            }
        }

        //把栈内剩余的运算符都弹出站
        for (int i = 0; i <= opStack.size(); i++) {
            sb.append(opStack.pop());
        }

        return sb;
    }

    public static void main(String[] args) {
        RpnMain rpnMain = new RpnMain();
        Scanner sc = new Scanner(System.in);

        while (true) {
            System.out.println("==========================\nPlease input an expression:");
            String input = sc.nextLine();

            if ("q".equals(input)) {
                sc.close();
                return;
            } else {
                if (rpnMain.isMatch(input)) {
                    System.out.println("The expression's brackets are matched");
                    // 获取逆波兰式
                    System.out.println(rpnMain.getRpn(input));
                } else {
                    System.out.println("Error: The expression's brackets are not matched! Enter 'q' to exit");
                }
            }
        }
    }
}

测试：