使用Hbuilder来打包自己的H5项目

第一步

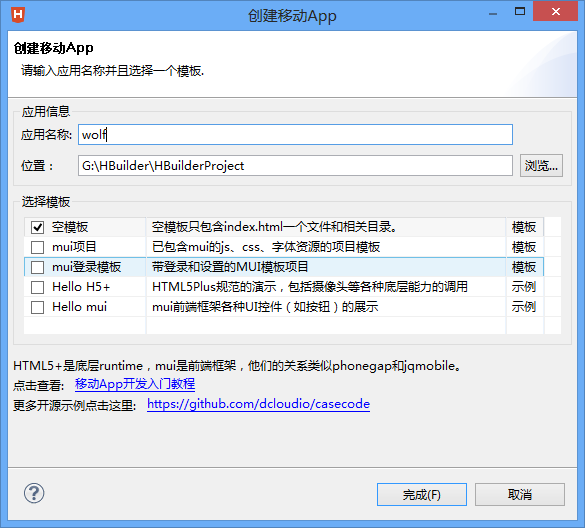
在Hbuilder上新建一个“移动APP”wolf（项目命名随意）
（如果没用引用mui框架的东西，“选择模板”中可以勾选“空模板”）

第二步

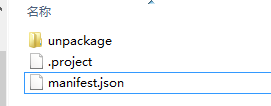
新建“空模板”项目wolf中，删除不必要的文件夹，只保留以下文件

第三步

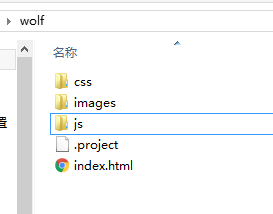
然后把你的H5项目里面相关的文件拷贝到Hbuilder中新建的项目wolf中
（自己的H5项目文件）


（拷贝到HBuilder中）

第四步

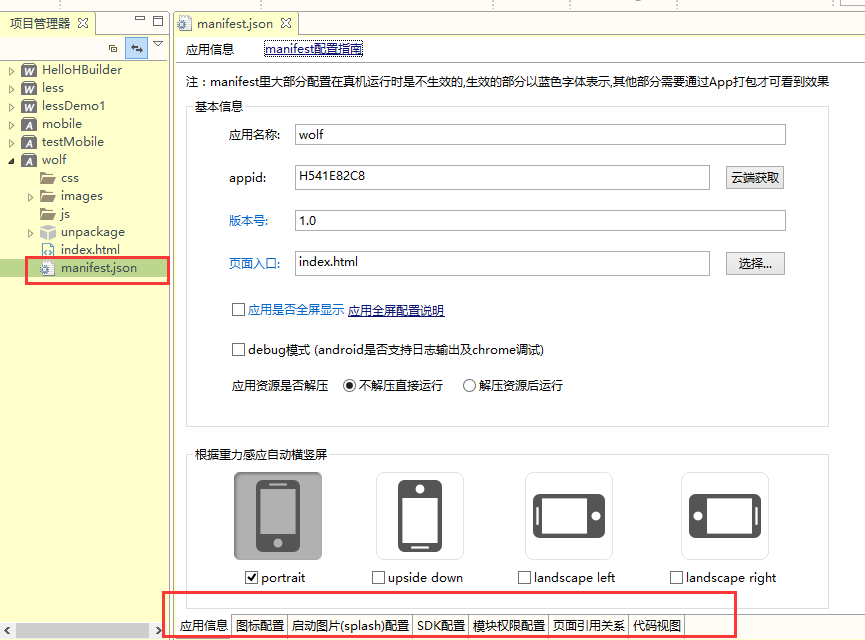
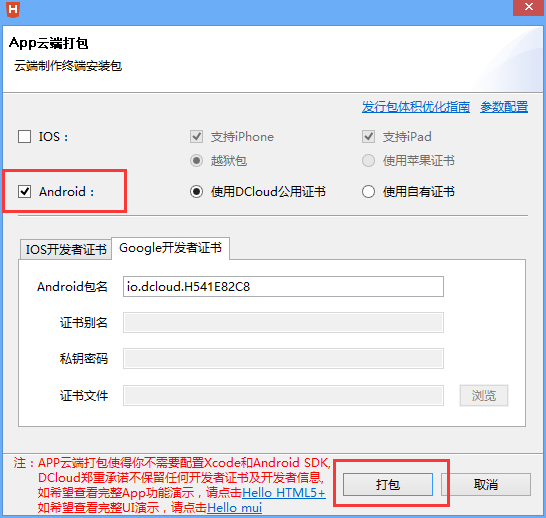
点击maifest.json配置文件，需要对截图中红色框里面相关的信息进行配置

第五步

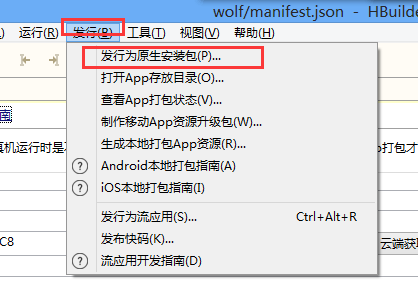
配置完相关的信息之后，点击选项卡“发行”-> "发行为原生安装包"，进行打包

第六步

截图为将项目打包成Android原生的app

打包成功截图：

使用Hbuilder打包app的更多相关文章

  1. 【原创分享·支付宝支付】HBuilder打包APP调用支付宝客户端支付

    前言 最近有点空余时间,所以,就研究了一下APP支付.前面很早就搞完APP的微信支付了,但是由于时间上和应用上的情况,支付宝一直没空去研究.然后等我空了的时候,发现支付宝居然升级了支付逻辑,虽然目前还 ...

  2. springboot+layui实现PC端用户的增删改查 & 整合mui实现app端的自动登录和用户的上拉加载 & HBuilder打包app并在手机端下载安装

    springboot整合web开发的各个组件在前面已经有详细的介绍,下面是用springboot整合layui实现了基本的增删改查. 同时在学习mui开发app,也就用mui实现了一个简单的自动登录和 ...

  3. hbuilder打包app基本流程

    声明:本文可能用到一些工具和第三方网站,都是为了达到目的而使用的工具,绝不含有广告成分 1.下载.最新的Hbuilder X貌似不能直接创建移动app了(自己不会用),建议旧版.可去腾某讯软件中心下载 ...

  4. HBuilder打包App方法

    HBuilder是DCloud(数字天堂)推出的一款支持HTML5的Web开发IDE.该软件既可以支持web代码编写,也可以将已经编写好的项目代码打包为手机APP. HBuilder提供的打包有云端打 ...

  5. HBuilder打包App流程记录

    摘要:基于HBuilder建立一个简单的移动app项目,并打包成apk,使用这套平台用H5开发真正的移动项目,相当于省去了原生部分的人力和工作配合,性能的话,后续我会基于这套技术开发相关的应用来验证, ...

  6. HBuilder打包app(vue项目)

    一.测试项目是否可以正确运行    指令:npm run dev 首先我们先建立一个vue的项目,本人用的是vue-cli随便建立的,然后运行项目 不必非得是像我这样的,这一步的目的只是测试一下咱们的 ...

  7. vue项目 使用Hbuilder打包app 设置沉浸式状态栏

    使用 Hbuilder新建好移动app项目后,mainfest.json这个文件里的 plus里设置 statusbar ..... "plus": { "statusb ...

  8. hbuilder 打包app简易教程

    1. 新建app 2. 新建弹窗面板中选择MUi登录模版 ps:在弹出的窗口,填入应用名称,根据需求选择项目位置,以及模板内容. 3. 检验app效果 菜单栏 -> 运行 -> 手机运行 ...

  9. vue 用huilder打包APP时，安卓按返回键就退出App改为按两次再退出App

    做vue项目时,用Hbuilder打包APP,在安卓下按返回键就是退出了APP,百度了下.都是使用到MUI来解决的,自己也记录下. 在main.js里面引入mui.js并使用. import mui ...

随机推荐

  1. Zemax评价函数经验小结

    2.4 风景透镜 为了说明一个简单的评价函数问题,我们演示一个真实风景透镜实例,这个风景镜有两个局部最优解,它大概是历史上第一个照相透镜,具有合理的大视场.它一开始是在一个成像暗箱(camera ob ...

  2. python高级 之(零) --- 重点难点

    生成式子 列表生成式 字典生成式 深浅拷贝 list0 = [12,24,34,32,[64,23]] # 浅拷贝:浅拷贝只是将最外层容器拷贝一份放在堆里面,内层的容器不会被拷贝还是使用原来的地址 l ...

  3. DNS简单搭建

    一.安装服务 设置主机名 [root@localhost named]# hostnamectl set-hostname k1.kk.cn [root@localhost named]# bash ...

  4. Linux C/C++基础 文件(中)

    1.ubuntu cat命令的实现 cat——查看或者合并文件内容 #include<stdio.h> int main(int argc,char* argv[]) { //1.打开文件 ...

  5. IDEA添加Lombok插件

    背景: 最近老大给了一个项目,是个雏.一看实体类就懵逼了,没有getter.setter和构造方法,导致service和controller全报红线,私有属性也没有注释.按规矩,心里先把这位前辈骂10 ...

  6. python 实现 灰色预测 GM(1,1)模型 灰色系统 预测 灰色预测公式推导

    来源公式推导连接 https://blog.csdn.net/qq_36387683/article/details/88554434 关键词:灰色预测 python 实现 灰色预测 GM(1,1)模 ...

  7. 【计算机视觉】背景建模--Vibe 算法优缺点分析

    一.Vibe 算法的优点 Vibe背景建模为运动目标检测研究邻域开拓了新思路,是一种新颖.快速及有效的运动目标检测算法.其优点有以下两点: 1.思想简单,易于实现.Vibe通常随机选取邻域20个样本为 ...

  8. 用grok拆分java日志

    1.假设一行日志内容如下: [root@VM_0_92_centos opt]# cat error.log -- ::,[ERROR ajp-nio--exec-](cn.com.al1.compo ...

  9. 菜鸟系列Fabric——Fabric 1.4共识机制(5)

    fabric 共识机制 由于fabric是分布式的系统,因此需要共识机制来保障各个节点以相同的顺序状态保存账本,达成一致性. 在当前fabric1.4版本中,存在三种共识机制,分别是solo,kafk ...

  10. 关于Java中excel表格导出的总结（Java程序导出模板和Java根据模板导出表格两种实现方式）

    导出excel通用模板(程序定义模板导出) 转载原文:https://www.jianshu.com/p/5c7b359a159c 如下代码,本方法主要用于程序定义模板格式,并导出文件.该方法将定义和 ...