HDU - 3556 - Continued Fraction

先上题目：

Continued Fraction

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 131072/65536 K (Java/Others)
Total Submission(s): 332    Accepted Submission(s): 106

Problem Description

Dumbear loves numbers very much.
One day Dumbear found that each number can be expressed as a continued fraction. See below.

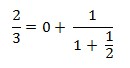
Formally, we say a number k can be expressed as a continued faction if

where a₀, a₁, …, a_n are positive integers except that a₀ maybe be 0 and a_n cannot be 1.
Dumbear also found a sequence which looks like the Farey sequence. Initially the sequence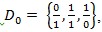and if we insert an element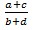between all the two adjacent element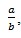,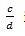in D_i, then we get a sequence D_i+1. So you can see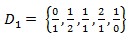and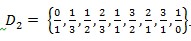Assume initially you are on the element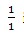in D₀, and if now you are on the element k in D_i, then if you go left(‘L’)(or right(‘R’)) you will be on the left(or right) element of k in D_i+1. So a sequence composed of ‘L’ and ‘R’ denotes a number. Such as ‘RL’ denotes the number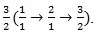 

Now give you a sequence composed of ‘L’ and ‘R’, you should print the continued fraction form of the number. You should use ‘-‘ to show the vinculum(the horizontal line), you should print one space both in front and back of ‘+’, and all parts up or down the vinculum should be right aligned. You should not print unnecessary space, ‘-‘ or other character. See details in sample.

 

Input

There are several test cases in the input.
For each test case, there is a single line contains only a sequence composed of ‘L’ and ‘R’. The length of the sequence will not exceed 10000.
The input terminates by end of file marker.

 

Output

For each test case, output the continued fraction form of the number which the input sequence denotes. The total amount of output will not exceed 4MB.

 

Sample Input

LR

RL

 

Sample Output

           1

0 + -----

           1

      1 + -

           2

     1

1 + -

     2

 

　　　　题意：给出一个只有L和R的字符串，根据它给出的定义移动，然后将最终的结果按照他给出的那种分式输出。

　　　　模拟+找规律。首先先根据它的定义模拟它的移动，然后可以根据自己的分析求出a[]数组的每一项是多少，然后在按照它的格式输出。这里求a[]数组分析一下就可以知道怎么怎么求了，然后关于输出，通过前后项的长度关系就可以得出要输出多少个空格多少'-'了，但是这样做的话直接提交可能会wa，这里可以通过输出前几项找一下规律。将L,LL,LR,LLL,LLR,LRL,LRR以及R,RL,RR,RLL,RLR,RRL,RRR(也就是前几项的变化的输有情况)输出，然后通过观察，我们可以发现，对于第2项开始，如果当前项等于前一项，那么a[tot]++,否则a[tot]--;tot++;a[tot]=2;当前其实如果写得好的话可以顺便把前一项的情况也包含在公式里面。然后直接构造a[]，在打印，速度和准确性上面都会有保证。

 

上代码：

 

 #include <cstdio>
 #include <cstring>
 #include <string>
 #include <algorithm>
 #define MAX 10002
 #define PUTS(M,x) for(int k=0;k<M;k++) putchar(x)
 #define ll long long
 using namespace std;

 char c[MAX];
 int l;
 ll a[MAX];
 char ss[MAX<<][];
 int len[MAX];
 int tot;
 typedef struct{
     ll fz,fm;
 }fs;

 fs A[],p;

 void cons(int l){
     if(c[]=='L'){
         a[]=; a[]=; tot=;
     }else{
         a[]=; tot=;
     }
     for(int i=;i<l;i++){
         if(c[i]==c[i-]) a[tot]++;
         else{
             a[tot]--;
             a[++tot]=;
         }
     }
     tot++;
 }

 int main()
 {
     int M;
     //freopen("data.txt","r",stdin);
     while(scanf("%s",c)!=EOF){
         l=strlen(c);
 //        A[0].fz=0;  A[0].fm=1;
 //        A[1].fz=1;  A[1].fm=1;
 //        A[2].fz=1;  A[2].fm=0;
 //        for(int i=0;i<l;i++){
 //            if(c[i]=='L'){
 //                A[2]=A[1];
 //            }else{
 //                A[0]=A[1];
 //            }
 //            A[1].fz=A[0].fz+A[2].fz;
 //            A[1].fm=A[0].fm+A[2].fm;
 //        }
 //        tot=0;
 //        p=A[1];
 //        while(1){
 //            a[tot]=p.fz/p.fm;
 //            sprintf(ss[tot],"%I64d",a[tot]);
 //            tot++;
 //            p.fz=p.fz%p.fm;
 //            if(p.fz==0) break;
 //            else if(p.fz==1){
 //                a[tot]=p.fm;
 //                sprintf(ss[tot],"%I64d",a[tot]);
 //                tot++;
 //                break;
 //            }
 //            swap(p.fz,p.fm);
 //        }
         cons(l);
         for(int i=;i<tot;i++) sprintf(ss[i],"%I64d",a[i]);
         len[tot-]=strlen(ss[tot-]);
         len[tot-]=strlen(ss[tot-]) +  + strlen(ss[tot-]);
         for(int i=tot-;i>=;i--){
             len[i]=strlen(ss[i]) +  + len[i+];
         }

 //        for(int i=0;i<tot;i++) printf("%I64d ",a[i]);
 //        printf("\n");
 //        for(int i=0;i<tot;i++) printf("%d ",len[i]);
 //        printf("\n");
         M=len[];
         for(int i=;i<tot-;i++){
             PUTS(M-,' ');  putchar('');   putchar('\n');
             PUTS(M-len[i],' ');
             printf("%s + ",ss[i]);
             PUTS(len[i+],'-');
             putchar('\n');
         }
         PUTS(M-(int)strlen(ss[tot-]),' ');
         printf("%s",ss[tot-]);
         printf("\n");
     }
     return ;
 }

/*3556*/