数学分析告诉偶们什么（vamei）

1】人生的痛苦在于追求错误的东西。所谓追求错误的东西，就是你在无限趋近于它的时候，才猛然发现，你和它是不连续的。

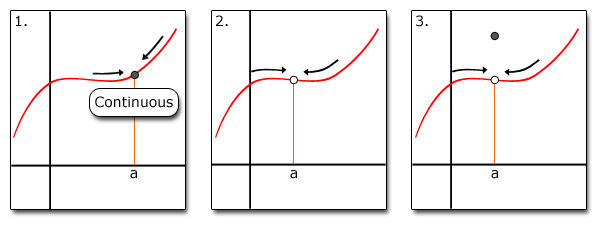
2】人和人就像数轴上的有理数点，彼此能够靠得非常近非常近，但你们之间始终存在隔阂。

3】人是不孤独的。正如数轴上有无限多个有理点，在你的随意一个小邻域内都能够找到你的伙伴。但人又是寂寞的，正如把整个数轴的无理点标记上以后。就一个人都见不到了。

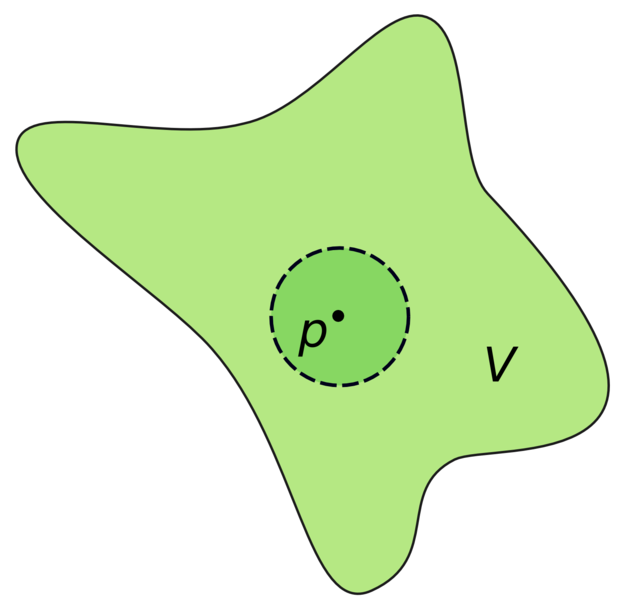
4】人和命运的关系就像F(x)=x与G(x)=x2的关系。一開始。你以为命运是你的无穷小量。随着年龄的增长，你才发现你用尽全力也赶不上命运的步伐。这时候。若不是以一种卑微的姿态走下去，便是结束自己的生命。

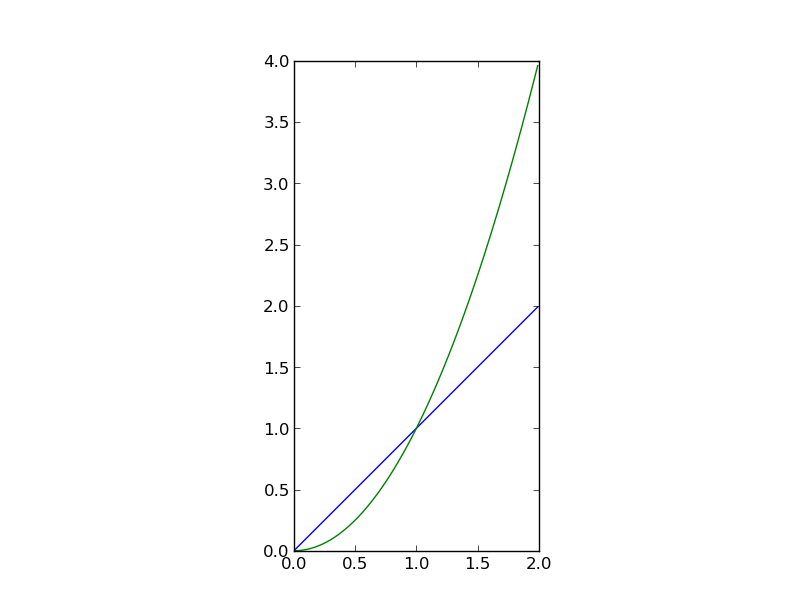
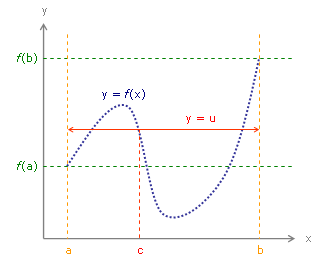
5】零点存在定理告诉我们，哪怕你和他站在对立面，仅仅要你们的心还是连续的，你们就能找到你们的平衡点。

6】人生是一个级数，理想是你渴望收敛到的那个值。不必太在意，由于我们要认识到有限的人生刻画不出无穷的级数。收敛也仅仅是一个梦想罢了。不如脚踏实地，经营好每一天吧。

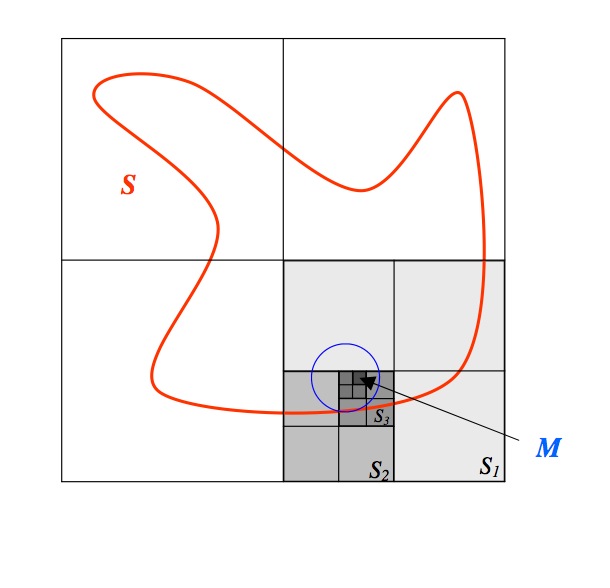
7】有限覆盖定理告诉我们，一件事情假设是能够实现的，那么你仅仅要投入有限的时间和精力就一定能够实现。至于那些在你能力范围之外的事情。就随他去吧。

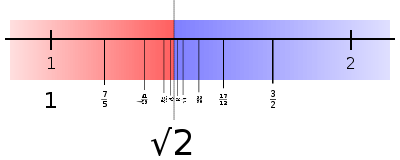
8】痛苦的回顾是能够缩小的，但不可能消亡。区间套最后套出的那一个点在整个区间上微不足道，但一定是存在的，并且刻骨铭心。

9】我们曾有多少的理想和承诺，在经历几次求导的考验之后就面目全非甚至荡然无存？有没有那么一个誓言，叫做f(x)=ex？

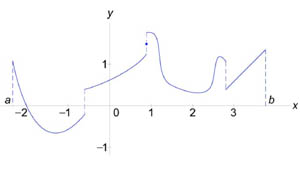
10】幸福是可积的。有限的间断点并不影响它的积累。

所以，乐观地面对人生吧~

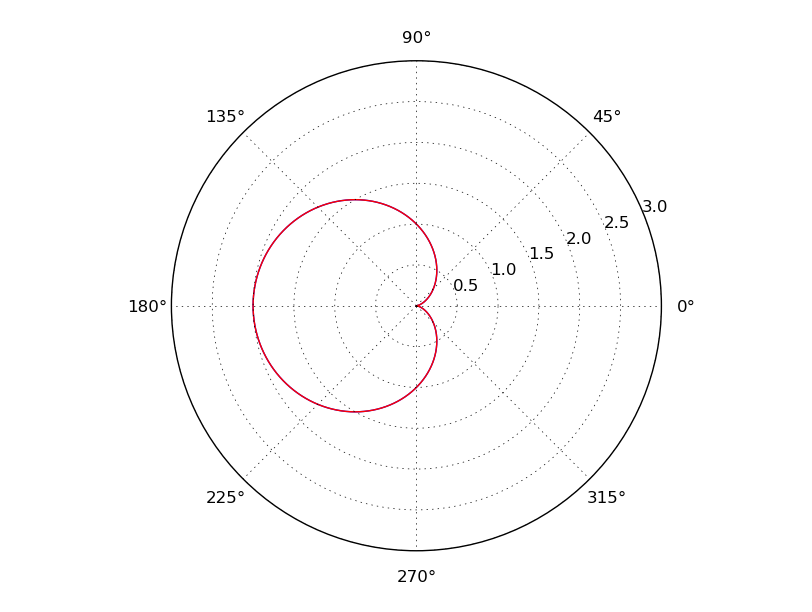
11】r=a(1−cosθ) 我写的这个函数，谁能看得懂呢？